Skip to main content
SpringerLink
Log in

Numerical Identification of the Fractional Derivatives in the Two-Dimensional Fractional Cable Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

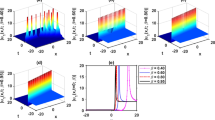
In this paper, the two-dimensional fractional cable equation is considered, an efficient numerical method to obtain the identification of the fractional derivatives is investigated. Concerning the numerical treatment of the two-dimensional fractional cable equation, a fourth-order compact finite difference method is proposed, the stability and convergence of the compact difference method are discussed rigorously by means of the Fourier method. For the inverse problem of the identification of the fractional derivatives, Levenberg–Marquardt iterative method is employed, and the fractional sensitivity equation is obtained by means of the digamma function. Finally, numerical examples are presented to show the effectiveness of the proposed numerical method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus. World Scientific, New Jersey (2012)

    MATH  Google Scholar 

  2. Battaglia, J.L., Cois, O., Puigsegur, L., Oustaloup, A.: Solving an invese heat conduction problem using a non-integer identified model. Int. J. Heat Mass Transf. 44, 2671–2680 (2001)

    Article  MATH  Google Scholar 

  3. Bhrawy, A.H., Zaky, M.A.: Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 80, 101–116 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chen, C.M., Liu, F., Burrage, K.: Finite difference methods and a Fourier analysis for the fractional reaction–subdiffusion equation. Appl. Math. Comput. 198(2), 754–769 (2008)

    MathSciNet  MATH  Google Scholar 

  5. Chen, C.M., Liu, F., Burrage, K.: Numerical analysis for a variable-order nonlinear cable equation. J. Comput. Appl. math. 236(2), 209–224 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cheng, J., Nakagawa, J., Yamamoto, M., Yamazaki, T.: Uniqueness in an inverse problem for a one-dimensional fractional diffusion equation. Inverse Probl. 25, 115002 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cui, M.R.: Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 228(20), 7792–7804 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Deng, W.: Numerical algorithm for the time fractional Fokker–Planck equation. J. Comput. Phys. 227(2), 1510–1522 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. Deng, W., Hesthaven, J.S.: Local discontinuous Galerkin methods for fractional diffusion equations. ESAIM Math. Model. Numer. Anal. 47, 1845–1864 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Diethelm, K., Ford, N.J., Freed, A.D., Luchko, Yu.: Algorithms for the fractional calculus: a selection of numerical methods. Comput. Methods Appl. Mech. Eng. 194, 743–773 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  11. Ghazizadeh, H.R., Azimi, A., Maerefat, M.: An inverse problem to estimate relaxation parameter and order of fractionality in fractional single-phase-lag heat equation. Int. J. Heat Mass Transf. 55, 2095–2101 (2012)

    Article  Google Scholar 

  12. Henry, B.I., Langlands, T.A.M., Wearne, S.L.: Fractional cable models for spiny neuronal dentrites. Phys. Rev. Lett. 100, 128103 (2008)

    Article  Google Scholar 

  13. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Book  MATH  Google Scholar 

  14. Hu, X., Zhang, L.: Implicit compact difference schemes for the fractional cable equation. Appl. Math. Model. 36, 4027–4043 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Hsu, P.T., Chu, Y.H.: An inverse non-Fourier heat conduction problem approach for estimating the boundary condition in electronic device. Appl. Math. Model. 28, 639–652 (2004)

    Article  MATH  Google Scholar 

  16. Jiang, X.Y., Qi, H.T.: Thermal wave model of bioheat transfer with modified Riemann–Liouville fractional derivative. J. Phys. A 45(48), 485101 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jiang, X.Y., Xu, M.Y., Qi, H.T.: The fractional diffusion model with an absorption term and modified Fick’s law for non-local transport processes. Nonlinear Anal. 11(1), 262–269 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Langlands, T.A.M., Henry, B.I., Wearne, S.L.: Fractional cable equation models for anomalous electrodiffusion in nerve cells: infinite domain solutions. J. Math. Biol. 59, 761–808 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Langlands, T.A.M., Henry, B.I., Wearne, S.L.: Fractional cable equation models for anomalous electrodiffusion in nerve cells: finite domain solutions. SIAM J. Appl. Math. 71(4), 1168–1203 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Li, C.P., Zhao, Z., Chen, Y.Q.: Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion. Comput. Math. Appl. 62(3), 855–875 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Lin, Y.M., Li, X.J., Xu, C.J.: Finite difference/spectral approximations for the fractional cable equation. Math. Comput. 80(275), 1369–1396 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  22. Liu, F., Yang, Q., Turner, I.: Two new implicit numerical methods for the fractional cable equation. J. Comput. Nonlinear Dyn. 6, 0110091–0110097 (2011)

    Google Scholar 

  23. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 172(1), 65–77 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  24. Meerschaert, M.M., Scheffler, H.P., Tadjeran, C.: Finite difference methods for two-dimensional fractional dispersion equation. J. Comput. Phys. 211(1), 249–261 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  25. Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339(1), 1–77 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  26. Murio, D.A.: Time fractional IHCP with Caputo fractional derivatives. Comput. Math. Appl. 56, 2371–2381 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  27. Oldham, K., Spanier, J.: The fractional calculus. Academic Press, New York (1974)

  28. Özisik, M.N.: Inverse Heat Transfer: Fundamentals and Applications. CRC Press, Boca Raton (2000)

    Google Scholar 

  29. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  30. Quintana-Murillo,J., Yuste, S.B.: An explicit numerical method for the fractional cable equation. Int. J. Differ. Equ. 2011, 231920 (2011)

  31. Sun, H., Chen, W., Li, C., Chen, Y.: Finite difference schemes for variable-order time fractional diffusion equation. Int. J. Bifurc. Chaos 22(4), 1250085 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  32. Sun, Z.Z., Wu, X.: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56, 193–209 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  33. Yu, B., Jiang, X.Y., Xu, H.: A novel compact numerical method for solving the two-dimensional non-linear fractional reaction-subdiffusion equation. Numer. Algor. 68, 923–950 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. Yu, B., Jiang, X.Y., Qi, H.: An inverse problem to estimate an unknown order of a Riemann–Liouville fractional derivative for a fractional Stokes first problem for a heated generalized second grade fluid. Acta Mech. Sin. 31, 153–161 (2015)

    Article  MathSciNet  Google Scholar 

  35. Yu, B., Jiang, X.Y.: A fractional anomalous diffusion model and numerical simulation for sodium ion transport in the intestinal wall. Adv. Math. Phys. 2013, 479634 (2013)

  36. Zhang, Y., Sun, Z.: Error analysis of a compact ADI scheme for the 2D fractional subdiffusion equation. J. Sci. Comput. 59, 104–128 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhang, Y., Xu, X.: Inverse source problem for a fractional diffusion equation. Inverse Probl. 27, 035010 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  38. Zhang, H., Yang, X., Han, H.: Discrete - time orthogonal spline collocation method with application to two-dimensional fractional cable equation. Comput. Math. Appl. 68, 1710–1722 (2014)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors wish to express their thanks to the Editor and the anonymous referees for their fruitful advice and comments. The authors express their sincere thanks to Professor Mingrong Cui for his discussion. The project was supported by the National Natural Science Foundation of China (11472161, 11102102 and 91130017) and the Natural Science Foundation of Shandong Province (ZR2015AM011).

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, China

    Bo Yu & Xiaoyun Jiang

Authors
  1. Bo Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoyun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaoyun Jiang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, B., Jiang, X. Numerical Identification of the Fractional Derivatives in the Two-Dimensional Fractional Cable Equation. J Sci Comput 68, 252–272 (2016). https://doi.org/10.1007/s10915-015-0136-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0136-y

Keywords

Search

Navigation