Convergence Analysis in the Maximum Norm of the Numerical Gradient of the Shortley–Weller Method

Abstract

The Shortley–Weller method is a standard central finite-difference-method for solving the Poisson equation in irregular domains with Dirichlet boundary conditions. It is well known that the Shortley–Weller method produces second-order accurate solutions and it has been numerically observed that the solution gradients are also second-order accurate; a property known as super-convergence. The super-convergence was proved in the $L^{2}$ norm in Yoon and Min (J Sci Comput 67(2):602–617, 2016). In this article, we present a proof for the super-convergence in the $L^{\infty }$ norm.

Appendix: Detailed Calculations in Lemma 4.3

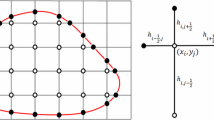
In this section, we provide detailed calculations that lead to the estimate $\left\| D_{x}^{h}c^{h}\right\| _{L^{\infty }\left( \tilde{\Omega _{o}^{h}}\right) }\le \frac{105}{4}\max _{\tilde{\Omega },\left| \alpha \le 5\right| }\left| \partial ^{\alpha }u\right| \cdot h^{2}$ in Lemma 4.3.

Using the Taylor series of $u\left( x,y\right)$ at $\left( x_{i+\frac{1}{2}},y_{j}\right) ,$ the terms that sum up $D_{x}^{h}c^{h}$ in (4) are expanded. For notational conveniences, the local coordinates centered at $\left( x_{i+\frac{1}{2}},y_{j}\right)$ are used in the calculations. For example, $u_{i+1,j+1}$ is denoted by $u\left( \frac{h}{2},h\right)$. The Taylor expansions are listed below with remainders.

$$\begin{aligned} \begin{array}{rrrrrrrrrrr} u\left( \pm \frac{3h}{2},0\right) =u &{} \pm &{} \frac{3h}{2}u_{x} &{} + &{} \frac{9h^{2}}{8}u_{xx} &{} \pm &{} \frac{9h^{3}}{16}u_{xxx} &{} + &{} \frac{27h^{4}}{128}u_{xxxx} &{} \pm &{} \frac{81h^{5}}{1280}u_{xxxxx}\left( \xi _{1}^{\pm },0\right) \\ u\left( \pm \frac{h}{2},0\right) =u &{} \pm &{} \frac{h}{2}u_{x} &{} + &{} \frac{h^{2}}{8}u_{xx} &{} \pm &{} \frac{h^{3}}{48}u_{xxx} &{} + &{} \frac{h^{4}}{384}u_{xxxx} &{} \pm &{} \frac{h^{5}}{3840}u_{xxxxx}\left( \xi _{2}^{\pm },0\right) \end{array}\\ \begin{array}{rrrrrcc} \Delta u\left( \pm \frac{h}{2},0\right) =\Delta u&\pm&\frac{h}{2}\left( u_{xxx}+u_{xyy}\right)+ & {} \frac{h^{2}}{8}\left( u_{xxxx}+u_{xxyy}\right)&\pm&\frac{h^{3}}{48}\left( u_{xxxxx}+u_{xxxyy}\right) \left( \xi _{4}^{\pm },0\right) \end{array} \end{aligned}$$

When the above expansions are inserted into the summation of $D_{x}^{h}c^{h}$, canceled out all the terms but the remainders.

$$\begin{aligned} D_{x}^{h}c_{i+\frac{1}{2},j}^{h}{=}\frac{h^{2}}{120}\left( \begin{array}{l} {-}\left( \frac{3}{2}\right) ^{5}\left( u_{xxxxx}\left( \xi _{1}^{+},0\right) {+}u_{xxxxx}\left( \xi _{1}^{-},0\right) \right) {+}\frac{5}{2^{5}}\left( u_{xxxxx}\left( \xi _{2}^{+},0\right) {+}u_{xxxxx}\left( \xi _{2}^{-},0\right) \right) \\ -\left( \frac{1}{2}\right) ^{5}\left( \begin{array}{r} \left( u_{xxxxx}{+}u_{xxxxy}{+}u_{xxxyy}{+}u_{xxyyy}{+}u_{xyyyy}{+}u_{yyyyy}\right) \left( \frac{1}{2}\xi _{3}^{+,+},\xi _{3}^{+}\right) \\ {+}\left( u_{xxxxx}{-}u_{xxxxy}{+}u_{xxxyy}{-}u_{xxyyy}{+}u_{xyyyy}{-}u_{yyyyy}\right) \left( \frac{1}{2}\xi _{3}^{+,-},\xi _{3}^{-}\right) \\ {+}\left( u_{xxxxx}{-}u_{xxxxy}{+}u_{xxxyy}{-}u_{xxyyy}{+}u_{xyyyy}{-}u_{yyyyy}\right) \left( \frac{1}{2}\xi _{3}^{-,+},\xi _{3}^{+}\right) \\ {+}\left( u_{xxxxx}{+}u_{xxxxy}{+}u_{xxxyy}{+}u_{xxyyy}{+}u_{xyyyy}{+}u_{yyyyy}\right) \left( \frac{1}{2}\xi _{3}^{-,-},\xi _{3}^{-}\right) \end{array}\right) \\ +\frac{5}{2}\left( \left( u_{xxxxx}+u_{xxxyy}\right) \left( \xi _{4}^{+},0\right) +\left( u_{xxxxx}+u_{xxxyy}\right) \left( \xi _{4}^{-},0\right) \right) \end{array}\right) \end{aligned}$$

Now, we prove the lemma.

$$\begin{aligned} \begin{array}{rcl} \left| D_{x}^{h}c_{i+\frac{1}{2},j}^{h}\right| &{} \le &{} \max _{\tilde{\Omega },\left| \alpha \right| \le 5}\left| \partial ^{\alpha }u\right| \cdot \frac{h^{2}}{120}\left( 2\cdot \left( \frac{3}{2}\right) ^{5}+2\cdot \frac{5}{2^{5}}+4\cdot 6\cdot \left( \frac{1}{2}\right) ^{5}+2\cdot 2\cdot \frac{5}{2}\right) \\ &{} = &{} \frac{105}{4}\max _{\tilde{\Omega },\left| \alpha \le 5\right| }\left| \partial ^{\alpha }u\right| \cdot h^{2}. \end{array} \end{aligned}$$