Skip to main content
SpringerLink
Log in

A Rigorous Condition Number Estimate of an Immersed Finite Element Method

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

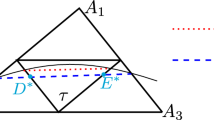
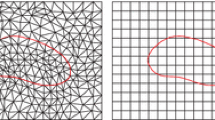
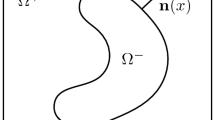
It is known that the convergence rate of the traditional iteration methods like the conjugate gradient method depends on the condition number of the stiffness matrix. Moreover the construction of fast solvers like multigrid and domain decomposition methods also need to estimate the condition number of the stiffness matrix. The main purpose of this paper is to give a rigorous condition number estimate of the stiffness matrix resulting from the linear and bilinear immersed finite element approximations of the high-contrast interface problem. It is shown that the condition number is \(C\rho h^{-2}\), where \(\rho \) is the jump of the discontinuous coefficients, h is the mesh size, and the constant C is independent of \(\rho \) and the location of the interface on the triangulation. Numerical results are also given to verify our theoretical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Burman, E.: Ghost penalty. C. R. Math. 348(21), 1217–1220 (2010)

    Article  MathSciNet  Google Scholar 

  2. Chen, Z., Zou, J.: Finite element methods and their convergence for elliptic and parabolic interface problems. Numer. Math. 79(2), 175–202 (1998)

    Article  MathSciNet  Google Scholar 

  3. Chou, S.-H., Kwak, D.Y., Wee, K.T.: Optimal convergence analysis of an immersed interface finite element method. Adv. Comput. Math. 33(2), 149–168 (2010)

    Article  MathSciNet  Google Scholar 

  4. Chu, C.-C., Graham, I., Hou, T.-Y.: A new multiscale finite element method for high-contrast elliptic interface problems. Math. Comput. 79(272), 1915–1955 (2010)

    Article  MathSciNet  Google Scholar 

  5. Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland Publishing Company, Amsterdam (1978)

    MATH  Google Scholar 

  6. Guo, R., Lin, T.: A group of immersed finite-element spaces for elliptic interface problems. IMA J. Numer. Anal. 39(1), 482–511 (2017)

    Article  MathSciNet  Google Scholar 

  7. Guo, R., Lin, T., Zhang, X.: Nonconforming immersed finite element spaces for elliptic interface problems. Comput. Math. Appl. 75(6), 2002–2016 (2018)

    Article  MathSciNet  Google Scholar 

  8. Guzmán, J., Sánchez, M.A., Sarkis, M.: A finite element method for high-contrast interface problems with error estimates independent of contrast. J. Sci. Comput. 73(1), 330–365 (2017)

    Article  MathSciNet  Google Scholar 

  9. He, X., Lin, T., Lin, Y.: Approximation capability of a bilinear immersed finite element space. Numer. Methods Partial Differ. Equ. 24(5), 1265–1300 (2008)

    Article  MathSciNet  Google Scholar 

  10. He, X., Lin, T., Lin, Y.: Immersed finite element methods for elliptic interface problems with non-homogeneous jump conditions. Int. J. Numer. Anal. Model. 8(2), 284–301 (2011)

    MathSciNet  MATH  Google Scholar 

  11. He, X., Lin, T., Lin, Y.: The convergence of the bilinear and linear immersed finite element solutions to interface problems. Numer. Methods Partial Differ. Equ. 28(1), 312–330 (2012)

    Article  MathSciNet  Google Scholar 

  12. Huang, P., Wu, H., Xiao, Y.: An unfitted interface penalty finite element method for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 323, 439–460 (2017)

    Article  MathSciNet  Google Scholar 

  13. Ji, H., Chen, J., Li, Z.: A symmetric and consistent immersed finite element method for interface problems. J. Sci. Comput. 61(3), 533–557 (2014)

    Article  MathSciNet  Google Scholar 

  14. Johansson, A., Larson, M.G.: A high order discontinuous Galerkin Nitsche method for elliptic problems with fictitious boundary. Numer. Math. 123(4), 607–628 (2013)

    Article  MathSciNet  Google Scholar 

  15. Li, Z., Lin, T., Lin, Y., Rogers, R.C.: An immersed finite element space and its approximation capability. Numer. Methods Partial Differ. Equ. 20(3), 338–367 (2004)

    Article  MathSciNet  Google Scholar 

  16. Li, Z., Lin, T., Wu, X.: New Cartesian grid methods for interface problems using the finite element formulation. Numer. Math. 96(1), 61–98 (2003)

    Article  MathSciNet  Google Scholar 

  17. Lin, T., Lin, Y., Zhang, X.: Partially penalized immersed finite element methods for elliptic interface problems. SIAM J. Numer. Anal. 53(2), 1121–1144 (2015)

    Article  MathSciNet  Google Scholar 

  18. Zhang, X.: Nonconforming immersed finite element methods for interface problems. Ph.D. thesis, Virginia Tech (2013)

  19. Zunino, P., Cattaneo, L., Colciago, C.M.: An unfitted interface penalty method for the numerical approximation of contrast problems. Appl. Numer. Math. 61(10), 1059–1076 (2011)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work of Saihua Wang and Xuejun Xu was supported by National Natural Science Foundation of China (Grant Nos. 11671302, 11871272). Feng Wang was supported by National Natural Science Foundation of China (Grant Nos. 11871281, 11871272). The author would like to thank the editor and the anonymous referees, who meticulously read through the paper and made valuable suggestions and comments which improve this paper greatly.

Author information

Authors and Affiliations

  1. School of Mathematical Science, Tongji University, Shanghai, 200092, China

    Saihua Wang & Xuejun Xu

  2. School of Mathematical Science, Nanjing Normal University, Nanjing, 210023, China

    Feng Wang

  3. Institute of Computational Mathematics, AMSS, Chinese Academy of Sciences, Beijing, 100190, China

    Xuejun Xu

Authors
  1. Saihua Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Feng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xuejun Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xuejun Xu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, S., Wang, F. & Xu, X. A Rigorous Condition Number Estimate of an Immersed Finite Element Method. J Sci Comput 83, 29 (2020). https://doi.org/10.1007/s10915-020-01212-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01212-1

Keywords

Search

Navigation