Skip to main content
SpringerLink
Log in

On a New Spatial Discretization for a Regularized 3D Compressible Isothermal Navier–Stokes–Cahn–Hilliard System of Equations with Boundary Conditions

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

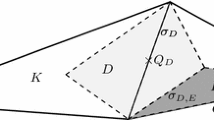
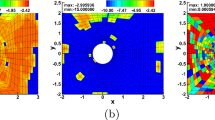
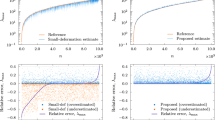
Abstract

We construct a new spatial finite-difference discretization for a regularized 3D Navier–Stokes–Cahn–Hilliard system of equations. The system can be attributed to phase field type models and describes flows of a viscous compressible isothermal two-component two-phase fluid with surface effects; the potential body force is also taken into account. In the discretization, the main sought functions are defined on one and the same mesh, and an original approximation of the solid wall boundary conditions (homogeneous with the discretization of equations) is suggested. The discretization has an important property of the total energy dissipativity allowing one to eliminate completely the so-called spurious currents. The discrete total mass and component mass conservation laws hold as well, and the discretization is also well-balanced for the equilibrium solutions. To ensure that the concentration C remains within the physically meaningful interval (0, 1), the non-convex part of the Helmholtz free energy is taken in a special logarithmic form (the Flory–Huggins potential). The speed of sound can depend on C that leads to different equilibrium mass densities of the “pure” phases. The results of numerical 3D simulations are also presented including those with a gravitational-type force. The positive role of the relaxation parameter is discussed too.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Availability of Data and Materials

The datasets generated during the current study are available from the corresponding author on reasonable request. They support our published claims and comply with field standards.

References

  1. Abu-Al-Saud, M.O., Popinet, S., Tchelepi, H.A.: A conservative and well-balanced surface tension model. J. Comput. Phys. 371, 896–913 (2018). https://doi.org/10.1016/j.jcp.2018.02.022

    Article  MathSciNet  MATH  Google Scholar 

  2. Adam, N., Franke, F., Aland, S.: A simple parallel solution method for the Navier–Stokes Cahn–Hilliard equations. Mathematics 8, 1224 (2020). https://doi.org/10.3390/math8081224

    Article  Google Scholar 

  3. Anderson, D.M., McFadden, G.B., Wheeler, A.A.: Diffuse-interface methods in fluid mechanics. Ann. Rev. Fluid Mech. 30, 139–165 (1998). https://doi.org/10.1146/annurev.fluid.30.1.139

    Article  MathSciNet  MATH  Google Scholar 

  4. Anna, S.L.: Droplets and bubbles in microfluidic devices. Ann. Rev. Fluid Mech. 48, 285–309 (2016). https://doi.org/10.1146/annurev-fluid-122414-034425

    Article  MathSciNet  MATH  Google Scholar 

  5. Balashov, V., Savenkov, E.: Quasi-hydrodynamic model of multiphase fluid flows taking into account phase interaction. J. Appl. Mech. Tech. Phys. 59, 434–444 (2018). https://doi.org/10.1134/S0021894418030069

    Article  MathSciNet  MATH  Google Scholar 

  6. Balashov, V.A., Savenkov, E.B.: Thermodynamically consistent spatial discretization of the one-dimensional regularized system of the Navier–Stokes–Cahn–Hilliard equations. J. Comput. Appl. Math. (2020). https://doi.org/10.1016/j.cam.2020.112743

    Article  MathSciNet  MATH  Google Scholar 

  7. Balashov, V., Savenkov, E., Zlotnik, A.: Numerical method for 3D two-component isothermal compressible flows with application to digital rock physics. Russ. J. Numer. Anal. Math. Model. 34, 1–13 (2019). https://doi.org/10.1515/rnam-2019-0001

    Article  MathSciNet  MATH  Google Scholar 

  8. Balashov, V., Zlotnik, A.: An energy dissipative spatial discretization for the regularized compressible Navier–Stokes–Cahn–Hilliard system of equations. Math. Model. Anal. 25, 110–129 (2020). https://doi.org/10.3846/mma.2020.10577

    Article  MathSciNet  Google Scholar 

  9. Balashov, V., Zlotnik, A.: An energy dissipative semi-discrete finite-difference method on staggered meshes for the 3D compressible isothermal Navier–Stokes–Cahn–Hilliard equations. J. Comput. Dyn. 7, 291–312 (2020). https://doi.org/10.3934/jcd.2020012

    Article  MathSciNet  MATH  Google Scholar 

  10. Balashov, V., Zlotnik, A., Savenkov, E.: Analysis of a regularized model for the isothermal two-component mixture with the diffuse interface. Russ. J. Numer. Anal. Math. Model. 32, 347–358 (2017). https://doi.org/10.1515/rnam-2017-0033

    Article  MathSciNet  MATH  Google Scholar 

  11. Beebe, D.J., Mensing, G.A., Walker, G.M.: Physics and applications of microfluidics in biology. Ann. Rev. Biomed. Eng. 4, 261–286 (2006). https://doi.org/10.1146/annurev.bioeng.4.112601.125916

    Article  Google Scholar 

  12. Blunt, M.J.: Multiphase Flow in Permeable Media. A Pore-Scale Perspective. Imperial College of Science, London (2017)

    Book  Google Scholar 

  13. Chen, L., Kang, Q., Mu, Y., He, Y.-L., Tao, W.-Q.: A critical review of the pseudopotential multiphase lattice Boltzmann model: methods and applications. Int. J. Heat Mass Transf. 76, 210–236 (2014). https://doi.org/10.1016/j.ijheatmasstransfer.2014.04.032

    Article  Google Scholar 

  14. Chetverushkin, B.N.: Kinetic Schemes and Quasi-Gasdynamic System of Equations. CIMNE, Barcelona (2008)

    Google Scholar 

  15. Connington, K., Lee, T.: A review of spurious currents in the lattice Boltzmann method for multiphase flows. J. Mech. Sci. Technol. 26, 3857–3863 (2012). https://doi.org/10.1007/s12206-012-1011-5

    Article  Google Scholar 

  16. Copetti, M.I.M., Elliott, C.M.: Numerical analysis of the Cahn–Hilliard equation with a logarithmic free energy. Numer. Math. 63, 39–65 (1992). https://doi.org/10.1007/BF01385847

    Article  MathSciNet  MATH  Google Scholar 

  17. Elizarova, T.G.: Quasi-Gas Dynamic Equations. Springer, Berlin (2009)

    Book  Google Scholar 

  18. Elizarova, T.G., Zlotnik, A.A., Shil’nikov, E.V.: Regularized equations for numerical simulation of flows of homogeneous binary mixtures of viscous compressible gases. Comput. Math. Math. Phys. 59, 1832–1847 (2019). https://doi.org/10.1134/S0965542519110058

    Article  MathSciNet  MATH  Google Scholar 

  19. Frank, F., Liu, C., Alpak, F.O., Riviere, B.: A finite volume/discontinuous Galerkin method for the advective Cahn–Hilliard equation with degenerate mobility on porous domains stemming from micro-CT imaging. Comput. Geosci. 22, 543–563 (2018). https://doi.org/10.1007/s10596-017-9709-1

    Article  MathSciNet  MATH  Google Scholar 

  20. Gao, Y., He, X., Mei, L., Yang, X.: Decoupled, linear, and energy stable finite element method for the Cahn–Hilliard–Navier–Stokes–Darcy phase field model related databases. SIAM J. Sci. Comput. 40, B110–B137 (2018). https://doi.org/10.1137/16M1100885

    Article  MATH  Google Scholar 

  21. Gong, Y., Liu, X., Wang, Q.: Fully discretized energy stable schemes for hydrodynamic equations governing two-phase viscous fluid flows. J. Sci. Comput. 69, 921–945 (2016). https://doi.org/10.1007/s10915-016-0224-7

    Article  MathSciNet  MATH  Google Scholar 

  22. Guermond, J.-L., Popov, B.: Viscous regularization of the Euler equations and entropy principles. SIAM J. Appl. Math. 74, 284–305 (2014). https://doi.org/10.1137/120903312

    Article  MathSciNet  MATH  Google Scholar 

  23. Guo, Z., Lin, P., Lowengrub, J., Wise, S.M.: Mass conservative and energy stable finite difference methods for the quasi-incompressible Navier–Stokes–Cahn–Hilliard system: primitive variable and projection-type schemes. Comput. Methods Appl. Mech. Eng. 326, 144–174 (2017). https://doi.org/10.1016/j.cma.2017.08.011

    Article  MathSciNet  MATH  Google Scholar 

  24. Han, D., Brylev, A., Yang, X., Tan, Z.: Numerical analysis of second order, fully discrete energy stable schemes for phase field models of two-phase incompressible flows. J. Sci. Comput. 70, 965–989 (2017). https://doi.org/10.1007/s10915-016-0279-5

    Article  MathSciNet  MATH  Google Scholar 

  25. Harvie, D.J.E., Davidson, M.R., Rudman, M.: An analysis of parasitic current generation in volume of fluid simulations. Appl. Math. Model. 30, 1056–1066 (2006). https://doi.org/10.1016/j.apm.2005.08.015

    Article  MATH  Google Scholar 

  26. Hu, X., Cubaud, T.: From droplets to waves: periodic instability patterns in highly viscous microfluidic flows. J. Fluid Mech. (2020). https://doi.org/10.1017/jfm.2019.1009

    Article  MathSciNet  MATH  Google Scholar 

  27. Jacqmin, D.: Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 155, 96–127 (1999). https://doi.org/10.1006/jcph.1999.6332

    Article  MathSciNet  MATH  Google Scholar 

  28. Jamet, D., Torres, D., Brackbill, J.U.: On the theory and computation of surface tension: the elimination of parasitic currents through energy conservation in the second-gradient method. J. Comput. Phys. 182, 262–276 (2002). https://doi.org/10.1006/jcph.2002.7165

    Article  MATH  Google Scholar 

  29. Liu, J.: Thermodynamically Consistent Modeling and Simulation of Multiphase Flows, Ph.D. dissertation. The University of Texas at Austin, Austin (2014)

  30. Lowengrub, J., Truskinovsky, L.: Quasi-incompressible Cahn–Hilliard fluids and topological transitions. Proc. R. Soc. Lond. A 454, 2617–2654 (1998). https://doi.org/10.1098/rspa.1998.0273

    Article  MathSciNet  MATH  Google Scholar 

  31. Minjeaud, S.: An adaptive pressure correction method without spurious velocities for diffuse-interface models of incompressible flows. J. Comput. Phys. 236, 143–156 (2013). https://doi.org/10.1016/j.jcp.2012.11.022

    Article  MathSciNet  MATH  Google Scholar 

  32. Popov, M.V., Elizarova, T.G.: Smoothed MHD equations for numerical simulations of ideal quasi-neutral gas dynamic flows. Comput. Phys. Commun. 196, 348–361 (2015). https://doi.org/10.1016/j.cpc.2015.07.003

    Article  MATH  Google Scholar 

  33. Provatas, N., Elde, K.: Phase-field Methods in Material Science and Engineering. Willey-VCH, Weinheim (2010)

    Book  Google Scholar 

  34. Sheretov, YuV: Continuum Dynamics Under Spatiotemporal Averaging. RKhD, Moscow-Izhevsk (2009). (in Russian)

    Google Scholar 

  35. Shirokov, I.A., Elizarova, T.G.: Simulation of laminar-turbulent transition in compressible Taylor–Green flow basing on quasi-gas dynamic equations. J. Turbul. 15, 707–730 (2014). https://doi.org/10.1080/14685248.2014.927581

    Article  MathSciNet  Google Scholar 

  36. Strasser, P.J., Tierra, G., Dünweg, B., Lukáčová-Medvid’ová, M.: Energy-stable linear schemes for polymer-solvent phase field models. Comput. Math. Appl. 77, 125–143 (2019). https://doi.org/10.1016/j.camwa.2018.09.018

    Article  MathSciNet  MATH  Google Scholar 

  37. Wang, X., Kou, J., Cai, J.: Stabilized energy factorization approach for Allen–Cahn equation with logarithmic Flory–Huggins potential. J. Sci. Comput. (2020). https://doi.org/10.1007/s10915-020-01127-x

    Article  MathSciNet  MATH  Google Scholar 

  38. Yang, X., Zhang, G.: Convergence analysis for the invariant energy quadratization (IEQ) schemes for solving the Cahn–Hilliard and Allen–Cahn equations with general nonlinear potential. J. Sci. Comput. (2020). https://doi.org/10.1007/s10915-020-01151-x

    Article  MathSciNet  MATH  Google Scholar 

  39. Zacharov, I., Arslanov, R., Gunin, M., et al.: “Zhores”—Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology. Open Eng. 9, 512–520 (2019). https://doi.org/10.1515/eng-2019-0059

    Article  Google Scholar 

  40. Zlotnik, A.A.: Parabolicity of a quasi-hydrodynamic system of equations and the stability of its small perturbations. Math. Notes. 83, 610–623 (2008). https://doi.org/10.1134/S0001434608050040

    Article  MathSciNet  MATH  Google Scholar 

  41. Zlotnik, A.A.: Energy equalities and estimates for barotropic quasi-gasdynamic and quasi-hydrodynamic systems of equations. Comput. Math. Math. Phys. 50, 310–321 (2010). https://doi.org/10.1134/S0965542510020120

    Article  MathSciNet  MATH  Google Scholar 

  42. Zlotnik, A.A.: On conservative spatial discretizations of the barotropic quasi-gasdynamic system of equations with a potential body force. Comput. Math. Math. Phys. 56, 303–319 (2016). https://doi.org/10.1134/S0965542516020160

    Article  MathSciNet  MATH  Google Scholar 

  43. Zlotnik, A.A.: Entropy-conservative spatial discretization of the multidimensional quasi-gasdynamic system of equations. Comput. Math. Math. Phys. 57, 706–725 (2017). https://doi.org/10.1134/S0965542517020166

    Article  MathSciNet  MATH  Google Scholar 

  44. Zlotnik, A.: On the energy dissipative spatial discretization of the barotropic quasi-gasdynamic and compressible Navier–Stokes systems of equations in polar coordinates. Russ. J. Numer. Anal. Math. Model. 33, 199–210 (2018). https://doi.org/10.1515/rnam-2018-0017

    Article  MATH  Google Scholar 

  45. Zlotnik, A.A., Lomonosov, T.A.: Conditions for \(L^2\)-dissipativity of linearized explicit difference schemes with regularization for 1D barotropic gas dynamics equations. Comput. Math. Math. Phys. 59, 452–464 (2019). https://doi.org/10.1134/S0965542519030151

    Article  MathSciNet  MATH  Google Scholar 

  46. Zlotnik, A.A., Lomonosov, T.A.: On \(L^2\)-dissipativity of a linearized explicit finite-difference scheme with quasi-gasdynamic regularization for the barotropic gas dynamics system of equations. Dokl. Math. 101, 198–204 (2020). https://doi.org/10.1134/S1064562420030229

    Article  Google Scholar 

Download references

Funding

The study was supported by the Russian Science Foundation, Project No. 19-11-00169.

Author information

Authors and Affiliations

  1. NRU Higher School of Economics, Pokrovskii bd. 11, Moscow, Russia, 109028

    Alexander Zlotnik

  2. Keldysh Institute of Applied Mathematics, Miusskaya sqr. 4, Moscow, Russia, 125047

    Vladislav Balashov & Alexander Zlotnik

Authors
  1. Vladislav Balashov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander Zlotnik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexander Zlotnik.

Ethics declarations

Conflict of interest

There is no any conflict of interests/competing interests to declare that are relevant to the content of this article.

Code Availability (software application or custom code)

Our custom codes are not publicly available. They support our published claims and comply with field standards.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The study was supported by the Russian Science Foundation, Project No. 19-11-00169.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Balashov, V., Zlotnik, A. On a New Spatial Discretization for a Regularized 3D Compressible Isothermal Navier–Stokes–Cahn–Hilliard System of Equations with Boundary Conditions. J Sci Comput 86, 33 (2021). https://doi.org/10.1007/s10915-020-01388-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01388-6

Keywords

Mathematics Subject Classification

Search

Navigation