Stiffened Gas Approximation and GRP Resolution for Compressible Fluid Flows of Real Materials

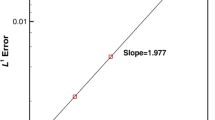
Abstract

The equation of state (EOS) embodies thermodynamic properties of compressible fluid materials and usually has very complicated forms in real engineering applications. The complexity of EOS in form gives rise to the difficulty in analyzing relevant wave patterns and in designing efficient numerical algorithms. In this paper, a strategy of local stiffened gas approximation is proposed for computing compressible fluid flows of real materials. The stiffened gas EOS is used to approximate general EOSs locally with certain thermodynamic compatibility at each interface of computational control volumes so that the exact Riemann solver can be significantly simplified and the computational cost of the resulting scheme is reduced up to two orders of magnitude. Then the generalized Riemann problem solver is further adopted not only to increase the accuracy and resolution but also to effectively reflect the thermodynamic effect through the inclusion of entropy variation into the numerical fluxes. The resulting scheme is demonstrated to be efficient and robust through typical numerical examples which display the excellent performance of such an approximation under extreme thermodynamics.

Appendices

The Details of the Stiffened Gas Approximate GRP Solver

In this appendix, we assume a typical configuration (Rarefaction-Contact-Shock) and extract the detailed formulation of the “two-material” stiffened gas GRP solver. As convention [3,4,5], the GRP solver consists four parts, consistent with the associated Riemann solver: (A) Resolution of rarefaction waves; (B) Tracking of shocks; (C) Bridge by contact discontinuity; and (D) The computation of the time derivative of density $\rho$. More details can be found in [17].

(A) Resolution of rarefaction waves.

The key idea is to resolve the singularity at (0, 0). It consists of three steps:

• (I) Measurement of the expansion of the rarefaction wave. Characteristic coordinates are applied to characterize the expansion of such a rarefaction wave. Let $\alpha (x,t)=C_1$ and $\beta (x,t)=C_2$ be the integral curves, respectively, of

  $$\begin{aligned} \displaystyle {\frac{dx}{dt}} =u+c, \ \ \ \displaystyle {\frac{dx}{dt}} =u-c. \end{aligned}$$

  Denote $\Theta (\beta ):=\frac{\partial t}{\partial \alpha }(0,\beta )$. Then we have

  $$\begin{aligned} \displaystyle {\frac{\Theta (\beta )}{\Theta (\beta _L)}} = \left( \displaystyle {\frac{c(0,\beta )}{c_L}}\right) ^{\frac{1}{2\mu _L^2}}, \ \ \ \mu _L^2=\mu ^2(\rho _L)=\frac{\gamma _L-1}{\gamma _L+1}, \end{aligned}$$

  where $\beta _L=u_L-c_L$, $c(0,\beta _*)=c_{*L}$ when $\beta _*=u_*-c_{*L}$.

• (II) The rate of entropy variation across curved rarefaction waves. Across the curved rarefaction wave associated with $u-c$, the entropy variation $T\partial S/\partial x(0,\beta )$ in the neighborhood of the singularity point has the change rate,

  $$\begin{aligned} \displaystyle {\frac{T \partial S/\partial x(0,\beta )}{T_LS_{L}'}} =\left( \frac{c(0,\beta )}{c_L}\right) ^{\frac{1}{\mu _L^2}+1}. \end{aligned}$$

  Given the initial state in (4.2), the initial variation of the entropy is known by the Gibbs relation (1.1),

  $$\begin{aligned} T_L S_{L}' = e_{L}'-\displaystyle {\frac{p_L}{\rho _L^2}} \rho _{L}'. \end{aligned}$$

• (III) The interaction of kinematics and thermodynamics. The entropy variation strongly affects the dynamics of kinematic variables. Apply (3.6) and return to the (x, t)-frame, then we have

  $$\begin{aligned} a_L\displaystyle {\frac{D u}{D t}}(0,\beta ) +b_L \displaystyle {\frac{D p}{Dt}}(0,\beta ) =d_L(0,\beta ), \end{aligned}$$

  where the total (material) derivative $D/Dt =\partial /\partial t+u\partial /\partial x$, $\theta (\beta )=c(0,\beta )/c_L$ and

  $$\begin{aligned}&a_L = 1, \ \ \ b_L = \displaystyle {\frac{1}{\rho (0,\beta ) c(0,\beta )}},\ \ \ \psi '_L=u'_L+\frac{1}{\rho _L c_L}p'_L+\frac{1}{c_L}T_LS'_L,\\&d_L=\left[ \displaystyle {\frac{1+\mu _L^2}{1+2\mu _L^2}} \left( \theta (\beta )\right) ^{1/(2\mu _L^2)}+\displaystyle {\frac{\mu _L^2}{1+2\mu _L^2}} \left( \theta (\beta )\right) ^{(1+\mu _L^2)/\mu _L^2}\right] T_LS'_L-c_L\left( \theta (\beta )\right) ^{1/(2\mu _L^2)} \psi '_L. \end{aligned}$$

(B) Tracking of the shock.

The resolution of the right shock consists of the singularity tracking technique and the Lax-Wendroff strategy. Let $x=x(t)$ be a shock with speed $\sigma =x'(t)$ and separate two states ${\textbf{U}}_R(x,t)$ in the wave front and ${\textbf{U}}_*(x,t)$ in the wave back. For the time being, denote ${\textbf{U}}_*(t) = {\textbf{U}}_*(x(t),t)$ and ${\textbf{U}}_R ={\textbf{U}}_R(x(t),t)$. Using the Rankine-Hugoniot relations, the singularity is tracked by making differentiation along the shock trajectory $x=x(t)$. Denote

$$\begin{aligned} \displaystyle {\frac{D_\sigma }{Dt }} = \displaystyle {\frac{\partial }{\partial t}} +\sigma \displaystyle {\frac{\partial }{\partial x}}. \end{aligned}$$

We specify to the shock associated with $u+c$. The tracking of the right shock can be divided into two steps.

• (I) The interaction of kinematics and thermodynamics. The Rankine-Hugoniot relations provide the relation between all thermodynamic variables

  $$\begin{aligned} \rho _*=G(p_*;p_R,\rho _R)&=\rho _R\cdot \frac{p_*+\mu _R^2p_R+(1+\mu _R^2)p^R_{\infty }}{p_R+\mu _R^2p_*+(1+\mu _R^2)p^R_{\infty }}, \end{aligned}$$

  (A.1)

  and interaction of kinematics and thermodynamics

  $$\begin{aligned}&u_*=u_R+\Phi (p_*;p_R,\rho _R)=u_R+(p_*-p_R)\Lambda ^{\frac{1}{2}}, \end{aligned}$$

  (A.2)

  where $\Lambda =(1-\mu _R^2)\tau _R/(p_*+\mu _R^2p_R+(1+\mu _R^2)p_{\infty }^R)$ and $\mu _R^2=\mu ^2(\rho _R)=\frac{\gamma _R-1}{\gamma _R+1}$.

• (II) Tracking the shock trajectory $x=x(t)$. Take the differentiation along the shock trajectory $x=x(t)$,

  $$\begin{aligned} \displaystyle {\frac{D_\sigma u_*}{Dt}} = \displaystyle {\frac{D_\sigma u_R}{Dt}} + \displaystyle {\frac{\partial \Phi }{\partial p_*}} \displaystyle {\frac{D_\sigma p_*}{Dt}} + \displaystyle {\frac{\partial \Phi }{\partial \rho _R}} \displaystyle {\frac{D_\sigma \rho _R}{Dt}} + \displaystyle {\frac{\partial \Phi }{\partial p_R}} \displaystyle {\frac{D_\sigma p_R}{Dt}}, \end{aligned}$$

  and the limit along the shock trajectory $x=x(t)$, we have

  $$\begin{aligned} a_R\left( \displaystyle {\frac{D u}{Dt}}\right) _* +b_R\left( \displaystyle {\frac{D p}{Dt}}\right) _* =d_R, \end{aligned}$$

  where the coefficients $a_R$, $b_R$ and $d_R$ are given in terms of the intermediate state ${\textbf{U}}_*$ and the initial data from the right,

  $$\begin{aligned} \begin{array}{l} a_R=1+\rho _{*R}(\sigma -u_*)\displaystyle {\frac{\partial \Phi }{\partial p_*}}(p_*;p_R,\rho _R),\\ b_R=-\left[ \displaystyle {\frac{\sigma -u_*}{\rho _{*R}c_{*R}^2}}+\displaystyle {\frac{\partial \Phi }{\partial p_*}}(p_*;p_R,\rho _R)\right] ,\\ d_R=L_p^R \cdot p_R'+L_u^R \cdot u_R'+L_{\rho }^R \cdot \rho _R'. \\ \end{array} \end{aligned}$$

  Here

  $$\begin{aligned} \begin{array}{l} L_p^R= -\displaystyle {\frac{1}{\rho _R}}+(\sigma -u_R)\displaystyle {\frac{\partial \Phi }{\partial p_R}}(p_*;p_R,\rho _R),\\ L_u^R= \sigma -u_R -\rho _R c_R^2\displaystyle {\frac{\partial \Phi }{\partial p_R}}(p_*;p_R,\rho _R)-\rho _R \displaystyle {\frac{\partial \Phi }{\partial \rho _R}}(p_*;p_R,\rho _R),\\ L_{\rho }^R= (\sigma -u_R)\displaystyle {\frac{\partial \Phi }{\partial \rho _R}}(p_*;p_R,\rho _R), \end{array} \end{aligned}$$

  and

  $$\begin{aligned} \begin{array}{l} \displaystyle {\frac{\partial \Phi }{\partial p_*}}=\frac{\sqrt{\Lambda }}{2}\frac{p_*+(1+2\mu _{R}^2)p_R+2(1+\mu _R^2)p^R_{\infty }}{(p_*+\mu _R^2p_R+(1+\mu _R^2)p^R_{\infty })^2},\\ \displaystyle {\frac{\partial \Phi }{\partial p_R}}=-\frac{\sqrt{\Lambda }}{2}[\frac{(\mu _R^2+2)p_*+\mu _R^2p_R+2(1+\mu _R^2)p^R_{\infty }}{p_*+\mu _R^2p_R+(1+\mu _R^2)p^R_{\infty }}],\\ \displaystyle {\frac{\partial \Phi }{\partial \rho _R}}=-\frac{p_*-p_R}{2\rho _R}\sqrt{\Lambda }. \end{array} \end{aligned}$$

(C) Bridge by contact discontinuity.

Thanks to the continuity property of u and p across the contact discontinuity, their material derivatives keep continuous, respectively. It turns out that the contact discontinuity bridges two sub-regions between the shock and the rarefaction waves,

$$\begin{aligned} \left\{ \begin{array}{l} a_L\left( \displaystyle {\frac{D u}{Dt}}\right) _* +b_L\left( \displaystyle {\frac{D p}{Dt}}\right) _* =d_L,\\ a_R\left( \displaystyle {\frac{D u}{Dt}}\right) _* +b_R\left( \displaystyle {\frac{D p}{Dt}}\right) _* =d_R. \end{array} \right. \end{aligned}$$

Solving this algebraic system provides $\left( \displaystyle {\frac{D u}{Dt}}\right) _*$ and $\left( \displaystyle {\frac{D p}{Dt}}\right) _*$, we obtain

$$\begin{aligned}&\left( \displaystyle {\frac{\partial u}{\partial t}}\right) _*=\left( \displaystyle {\frac{D u}{Dt}}\right) _*+\frac{u_*}{\rho _*c_*^2}\left( \displaystyle {\frac{D p}{Dt}}\right) _*,\\&\left( \displaystyle {\frac{\partial p}{\partial t}}\right) _*=\left( \displaystyle {\frac{D p}{Dt}}\right) _*+\rho _*u_*\left( \displaystyle {\frac{D u}{Dt}}\right) _*, \end{aligned}$$

where $(\rho _*,u_*,p_*)$ is the solution of the associated Riemann problem and $c_*=c(\rho _*,p_*)$.

(D) The computation of the time derivative of density $\rho$

If $u_*>0$, we return to the rarefaction wave by using $S_t=-uS_x$ to derive

$$\begin{aligned} (\frac{\partial \rho }{\partial t})_*&=c_{*L}^{-2}((\partial p/\partial t)_*+(\gamma _L-1)\rho _{*L}u_*T_LS_L^{\prime }(\frac{c_{*L}}{c_L})^{1+\frac{1}{\mu _L^2}}). \end{aligned}$$

If $u_*<0$, the limiting value $(\frac{\partial \rho }{\partial t})_*$ is derived by the Rankine-Hugoniot relation

$$\begin{aligned}&{\tilde{G}}(\rho _{*R},p_*;p_R,\rho _R)=\frac{p_*+\gamma _R p_{\infty }^R}{(\gamma _R-1)\rho _{*R}}-\frac{p_R+\gamma _R p_{\infty }^R}{(\gamma _R-1)\rho _R}-\frac{1}{2}(p_R+p_*)(\frac{1}{\rho _R}-\frac{1}{\rho _{*R}})=0,\\&(u_*-\sigma )H_1(\frac{\partial \rho }{\partial t})_*+(\frac{\sigma }{c_{*R}^2}H_1+u_*H_2)(\frac{Dp}{Dt})_*+H_2(u_*-\sigma )\rho _{*R}u_*(\frac{Du}{Dt})_*=\\&u_*((u_R-\sigma )H_3\rho '_R+(\rho _RH_3+\rho _R c_R^2H_4)u'_R+(u_R-\sigma )H_4p'_R), \end{aligned}$$

where

$$\begin{aligned}&H_1=\frac{\partial {\tilde{G}}}{\partial \rho _*}=-\frac{1}{2}\left( \frac{p_*}{\rho _{*R}^2\mu _R^2}+\frac{p_R}{\rho _{*R}^2}+(1+\frac{1}{\mu _R^2})\frac{p_{\infty }^R}{\rho _{*R}^2}\right) ,\\&H_2=\frac{\partial {\tilde{G}}}{\partial p_*} = \frac{1}{2}\left( \frac{1}{\rho _{*R}\mu _R^2}-\frac{1}{\rho _R}\right) ,\\&H_3=\frac{\partial {\tilde{G}}}{\partial \rho }=\frac{1}{2}\left( \frac{p_R}{\rho _R^2\mu _R^2}+\frac{p_*}{\rho _R^2}+(1+\frac{1}{\mu _R^2})\frac{p_{\infty }^R}{\rho _R^2}\right) ,\\&H_4=\frac{\partial {\tilde{G}}}{\partial p} =-\frac{1}{2}\left( \frac{1}{\rho _R\mu _R^2}-\frac{1}{\rho _{*R}}\right) . \end{aligned}$$

The HLLC Solver for General EOS and Its Second Order Extension

The HLLC approximate Riemann solver [30,31,32] is an extension of the HLL Riemann solver in [13] in order to avoid the excessive numerical dissipation of HLL for intermediate characteristic fields. It has been widely applied for the shallow water equations, the Euler equations and the augmented equations for multicomponent flows etc. A detailed review of the HLLC solver can be find in [35] and its second order extension is inspired by [14] for a two-phase model of reactive flow with general equation of state. Below we recall the version of a single material.

1.1 Wave Speed Estimates

A 3-wave model is assumed for the HLLC solver and the contact wave is included in the structure. The“pressure-based” wave speed estimate is adopted,

$$\begin{aligned}&V_L = u_L-\theta _L({\bar{p}}_*)c_L, V_R = u_R + \theta _r({\bar{p}}_*)c_R, \end{aligned}$$

(B.1)

$$\begin{aligned}&V_* = \frac{p_R-p_L+\rho _Lu_L(V_L-u_L)-\rho _Ru_R(V_R-u_R)}{\rho _L(V_L-u_L)-\rho _R(V_R-u_R)}, \end{aligned}$$

(B.2)

$$\begin{aligned}&{\bar{p}}_*=\frac{\rho _R c_R p_L+\rho _L c_L p_R-\rho _L c_L\rho _R c_R(u_R-u_L)}{\rho _L c_L+\rho _R c_R}, \end{aligned}$$

(B.3)

$$\begin{aligned}&\theta _i(p)=\left\{ \begin{array}{ll} 1, &{} if\ p\leqslant p_i,\\ (1+\frac{\gamma +1}{2\gamma }(\frac{p + p_{\infty }}{p_i + p_{\infty }}-1))^{\frac{1}{2}}, &{} if\ p>p_i. \end{array} \right. i=L,R. \end{aligned}$$

(B.4)

The parameters $\gamma$ and $p_{\infty }$ are derived by

$$\begin{aligned} \gamma = \frac{1}{2}(\gamma _L+\gamma _R),\ p_{\infty }=\frac{1}{2}(p_{\infty }^L+p_{\infty }^R), \end{aligned}$$

where $\gamma _i$ and $p_{\infty }^i$, $i=L$ or R, are the stiffened gas approximation (1.8) of the general EOS.

1.2 The HLLC Numerical Fluxes

For a first order scheme, the discretization of (2.1) can be written as

$$\begin{aligned} {\textbf{U}}_{j}^{n+1} ={\textbf{U}}_{j}^n -\displaystyle {\frac{\Delta t}{\Delta x}} [{\textbf{F}}_{j+\frac{1}{2}} - {\textbf{F}}_{j-\frac{1}{2}}]. \end{aligned}$$

The HLLC numerical flux is evaluated as

$$\begin{aligned} {\textbf{F}}_{j+\frac{1}{2}} = \left\{ \begin{array}{ll} F_L, &{} if\ 0\leqslant V_L,\\ F_{*L}, &{} if\ V_L<0\leqslant V_{*},\\ F_{*R}, &{} if\ V_*<0\leqslant V_{R},\\ F_{R}, &{} if\ V_{R}>0,\\ \end{array} \right. \end{aligned}$$

(B.5)

with

$$\begin{aligned}&F_{*L} = F_L+V_L(U_{*L}-U_L),\ F_{*R} = F_R+V_R(U_{*R}-U_R),\\&U_{*i} = \rho _i\frac{V_i-u_i}{V_i-V_*}Q,\ Q=(1,V_*,E_i+(V_*-u_i)(V_*+\frac{p_i}{\rho _i(V_i-u_i)}))^{\top }, \ \ i=L, R. \end{aligned}$$

1.3 Runge-Kutta Time-Stepping for HLLC Solver

The two-stage Runge-Kutta method is applied for the second order HLLC scheme. The spatial reconstruction is done by

$$\begin{aligned}&U_{j}^n(x) = U_{j}^n + (U_x)_{j}^n(x-x_j),\\&(U_x)_{j}^n = \frac{1}{\Delta x}minmod(U_{j+1}-U_j,U_j-U_{j-1}). \end{aligned}$$

Then the conservative quantities are updated by

$$\begin{aligned}&{\textbf{U}}_{j}^{*} = {\textbf{U}}_{j}^n -\displaystyle {\frac{\Delta t}{\Delta x}} [{\textbf{F}}_{j+\frac{1}{2}}^n - {\textbf{F}}_{j-\frac{1}{2}}^n],\\&{\textbf{U}}_{j}^{n+1} = {\textbf{U}}_{j}^n -\displaystyle {\frac{\Delta t}{2\Delta x}} [{\textbf{F}}_{j+\frac{1}{2}}^n - {\textbf{F}}_{j-\frac{1}{2}}^n] -\displaystyle {\frac{\Delta t}{2\Delta x}} [{\textbf{F}}_{j+\frac{1}{2}}^* - {\textbf{F}}_{j-\frac{1}{2}}^*]. \end{aligned}$$