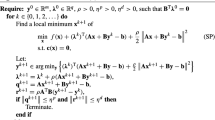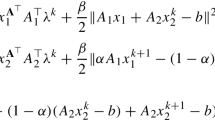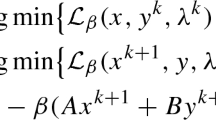Skip to main content
SpringerLink
Log in

On Glowinski’s Open Question on the Alternating Direction Method of Multipliers

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

The alternating direction method of multipliers was proposed by Glowinski and Marrocco in 1974, and it has been widely used in a broad spectrum of areas, especially in some sparsity-driven application domains. In 1982, Fortin and Glowinski suggested to enlarge the range of the dual step size for updating the multiplier from 1 to the open interval of zero to the golden ratio, and this strategy immediately accelerates the convergence of alternating direction method of multipliers for most of its applications. Meanwhile, Glowinski raised the question of whether or not the range can be further enlarged to the open interval of zero to 2; this question remains open with nearly no progress in the past decades. In this paper, we answer this question affirmatively for the case where both the functions in the objective function are quadratic. Thus, Glowinski’s open question is partially answered. We further establish the global linear convergence of the alternating direction method of multipliers with this enlarged step size range for the quadratic programming under a tight condition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. This is a translation from its original French version in 1982.

References

  1. Glowinski, R., Marrocco, A.: Sur l’approximation par éléments finis d’ordre un et la résolution par pénalisation-dualité d’une classe de problèmes de Dirichlet non linéaires. Revue Fr. Autom. Inf. Rech. Opér. Anal. Numér 2, 41–76 (1975)

    MATH  Google Scholar 

  2. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3, 1–122 (2010)

    Article  MATH  Google Scholar 

  3. Glowinski, R.: On alternating direction methods of multipliers: a historical perspective. In: Fitzgibbon, W., Kuznetsov, Y.A., Neittaanmaki, P., Pironneau, O. (eds.) Modeling, Simulation and Optimization for Science and Technology, Computational Methods in Applied Sciences, vol. 34, pp. 59–82. Springer, Dordrecht (2014)

    Google Scholar 

  4. Glowinski, R., Osher, S.J., Yin, W.T. (eds.): Splitting Methods for Communications and Imaging, Science and Engineering. Springer, Switzerland (2016)

    Google Scholar 

  5. Sun, J., Zhang, S.: A modified alternating direction method for convex quadratically constrained quadratic semidefinite programs. Eur. J. Oper. Res. 207, 1210–1220 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  6. Wen, Z.W., Goldfarb, D., Yin, W.T.: Alternating direction augmented Lagrangian methods for semidefinite programming. Math. Program. Comput. 2, 203–230 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Eckstein, J., Yao, W.: Augmented Lagrangian and alternating direction methods for convex optimization: a tutorial and some illustrative computational results. Pac. J. Optim. 11, 619–644 (2015)

    MathSciNet  Google Scholar 

  8. Fortin, M., Glowinski, R.: On decomposition-coordination methods using an augmented Lagrangian. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary Problems, pp. 97–146. North-Holland, Amsterdam (1983)

    Chapter  Google Scholar 

  9. Gabay, D.: Applications of the method of multipliers to variational inequalities. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrange Methods: Applications to the Solution of Boundary-valued Problems, pp. 299–331. North Holland, Amsterdam (1983)

    Chapter  Google Scholar 

  10. Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite-element approximations. Comput. Math. Appl. 2, 17–40 (1976)

    Article  MATH  Google Scholar 

  11. Glowinski, R.: Numerical Methods for Nonlinear Variational Problems. Springer, New York (1984)

    Book  MATH  Google Scholar 

  12. He, B.S., Ma, F., Yuan, X.M.: Convergence analysis of the symmetric version of ADMM. SIAM J. Imaging Sci. 9, 1467–1501 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  13. He, B.S., Yang, H.: Some convergence properties of a method of multipliers for linearly constrained monotone variational inequalities. Oper. Res. Lett. 23, 151–161 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  14. Xu, M.H.: Proximal alternating directions method for structured variational inequalities. J. Optim. Theory Appl. 134, 107–117 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Tao, M., Yuan, X.M.: On the \(O(1/t)\) convergence rate of alternating direction method with logarithmic-quadratic proximal regularization. SIAM J. Optim. 22, 1431–1448 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  16. Eckstein, J., Bertsekas, D.P.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55, 293–318 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  17. Eckstein, J., Fukushima, M.: Reformulations and applications of the alternating direction method of multipliers. In: Hager, W.W., Hearn, D.W., Pardalos, P.M. (eds.) Large Scale Optimization: State of the Art, pp. 115–134. Kluwer Academic Publishers, Dordrecht (1994)

    Chapter  Google Scholar 

  18. Gol’shtein, E.G., Tret’yakov, N.V.: Modified Lagrangian in convex programming and their generalizations. Math. Program. Stud. 10, 86–97 (1979)

    Article  MathSciNet  Google Scholar 

  19. Tao, M., Yuan, X.M.: The generalized proximal point algorithm with step size \(2\) is not necessarily convergent. Comput. Optim. Appl. 70, 827–839 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  20. He, B.S., Xu, M.H., Yuan, X.M.: Solving large-scale least squares covariance matrix problems by alternating direction methods. SIAM J. Matrix Anal. Appl. 32, 136–152 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  22. Powell, M.J.D.: A method for nonlinear constraints in minimization problems. In: Fletcher, R. (ed.) Optimization, pp. 283–298. Academic Press, New York (1969)

    Google Scholar 

  23. Rockafellar, R.T.: Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Math. Oper. Res. 1, 877–898 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  24. Martinet, B.: Regularisation, d’inéquations variationelles par approximations succesives. Rev. Francaise d’Inform. Recherche Oper. 4, 154–159 (1970)

    MATH  Google Scholar 

  25. Bergen, A.R.: Power Systems Analysis. Prentice Hall, Englewood Cliffs (1986)

    Google Scholar 

  26. Björck, A.: Numerical Methods for Least Squares Problems. SIAM, Philadelphia (1996)

    Book  MATH  Google Scholar 

  27. Bruckstein, A.M., Donoho, D.L., Elad, M.: From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Rev. 51, 34–81 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  28. Chua, L.O., Desoer, C.A., Kuh, E.S.: Linear and Nonlinear Circuits. McGraw-Hill, New York (1987)

    MATH  Google Scholar 

  29. Ehrgott, M., Winz, I.: Interactive decision support in radiation therapy treatment planning. OR Spectr. 30, 311–329 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Markowitz, H.M.: Porfolio Selection: Efficient Diversification of Investments. Wiley, New York (1959)

    Google Scholar 

  31. Tikhonov, A., Arsenin, V.: Solution of Ill-Posed problems. Winston, Washington (1977)

    MATH  Google Scholar 

  32. Chen, C.H., Li, M., Liu, X., Ye, Y.Y.: Extended ADMM and BCD for nonseparable convex minimization models with quadratic coupling terms: convergence analysis and insights. Math. Program. (2017). https://doi.org/10.1007/s10107-017-1205-9

    Google Scholar 

  33. Fiedler, M.: Bounds for the determinant of the sum of Hermitian matrices. Proc. Am. Math. Soc. 30, 27–31 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  34. Ding, J., Rhee, N.H.: On the equality of algebraic and geometric multiplicities of matrix eigenvalues. Appl. Math. Lett. 24, 2211–2215 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  35. He, B.S., Liao, L.Z., Han, D.R., Yang, H.: A new inexact alternating directions method for monotone variational inequalities. Math. Program. 92, 103–118 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  36. Eckstein, J.: Some saddle-function splitting methods for convex programming. Optim. Methods Softw. 4, 75–83 (1994)

    Article  MathSciNet  Google Scholar 

  37. Meyer, C.D.: Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia (2006)

    Google Scholar 

  38. Bhatia, R.: Matrix Analysis. Springer, New York (1997)

    Book  MATH  Google Scholar 

  39. Boley, D.: Local linear convergence of the alternating direction method of multipliers on quadratic or linear programs. SIAM J. Optim. 23, 2183–2207 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  40. Han, D.R., Yuan, X.M.: Local linear convergence of the alternating direction method of multipliers for quadratic programs. SIAM J. Numer. Anal. 51, 3446–3457 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  41. Bai, Z.Z., Tao, M.: Rigorous convergence analysis of alternating variable minimization with multiplier methods for quadratic programming problems with equality constraints. BIT 56, 399–422 (2016)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Min Tao was supported by the NSFC Grant: 11301280 and the Fundamental Research Funds for the Central Universities: 14380019. Xiaoming Yuan was supported by the General Research Fund from Hong Kong Research Grants Council: 12313516.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Key Laboratory for Novel Software Technology, Nanjing University, Jiangsu, China

    Min Tao

  2. Department of Mathematics, The University of Hong Kong, Hong Kong, China

    Xiaoming Yuan

Authors
  1. Min Tao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoming Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Min Tao.

Additional information

Communicated by Roland Glowinski.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tao, M., Yuan, X. On Glowinski’s Open Question on the Alternating Direction Method of Multipliers. J Optim Theory Appl 179, 163–196 (2018). https://doi.org/10.1007/s10957-018-1338-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-018-1338-x

Keywords

Mathematics Subject Classification

Search

Navigation