A Representation Result for Value-based Contraction

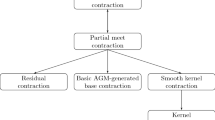
Abstract

Sven-Ove Hansson and Erik Olsson studied in Hansson and Olsson (Notre Dame Journal of Formal Logic, 36(1), 103–119 1995) the logical properties of an operation of contraction first proposed by Isaac Levi in Levi (1991). They provided a completeness result for the simplest version of contraction that they call Levi-contraction but left open the problem of characterizing axiomatically the more complex operation of value-based contraction or saturatable contraction. In this paper we propose an axiomatization for this operation and prove a completeness result for it. We argue that the resulting operation is better behaved than various rival operations of contraction defined in recent years.

Appendix

Lemma 17

Let K be a theory and let÷be a contraction operator for K that satisfies success, failure, and conjunctive inclusion.Then it satisfies conjunctive covering.

Proof

For any propositions α and β,consider the following cases. First, if ⊩ α ∧ β,then it follows that K ÷ (α ∧ β) = K by vacuity. Moreover, we have that ⊩ α which also implies that K ÷ α = K.Hence the claim holds in this case. Next, suppose that$\nvdash \alpha \wedge \beta$.According to success, we have that α ∧ β∉K ÷ (α ∧ β).Thus either α∉K ÷ (α ∧ β)or β∉K ÷ (α ∧ β).This implies that either K ÷ (α ∧ β) ⊆ K ÷ α or K ÷ (α ∧ β) ⊆ K ÷ β by conjunctive inclusion. □

Lemma 18

Let K be a theory and let÷be a relation-based saturatable contraction for K. Then it satisfies the postulate ofconjunctive reduction.

Proof

Assume that α ∈ K ÷ (α ∧ β). Andsuppose that x ∈ K ÷ β. Weneed to show that x ∈ K ÷ (α ∧ β).Consider the following cases.

Case 1::

If α∉K or β∉K,then it follows that α ∧ β∉K.Then by vacuity, we have that K ÷ (α ∧ β) = K.According to inclusion, we have that x ∈ K ÷ α ⊆ K = K ÷ (α ∧ β)as required.

Case 2::

If α ∈ K,β ∈ K,and ⊩ α ∧ β,then again by vacuity, we have that K ÷ (α ∧ β) = K.Similarly, it follows that x ∈ K ÷ α ⊆ K ÷ (α ∧ β)by inclusion.

Case 3::

Now consider the case that α,β ∈ K ∖ Cn(∅).Assume that x∉K ÷ (α ∧ β).It follows that there is some Z such thatx∉Z ∈ γ(S(K,α ∧ β)).Since $K\div (\alpha \wedge \beta )=\bigcap \gamma (S(K,\alpha \wedge \beta ))$,we have that K ÷ (α ∧ β) ⊆ Z.Thus it follows from α ∈ K ÷ (α ∧ β)that α ∈ Z.Furthermore, according to the definition of saturatable set, we have thatCn(Z ∪{¬(α ∧ β)})is maximally consistent. Hence, either β or ¬β belongs to Cn(Z ∪{¬(α ∧ β)}).

If β ∈ Cn(Z ∪{¬(α ∧ β)}), thenZ ⊩¬(α ∧ β) → β. From this itfollows that Z ⊩ β, since(¬(α ∧ β) → β) ≡ β. However, sinceα ∈ Z, it follows thatα ∧ β ∈ Z, which is contrary tothe assumption that Z ∈ S(K,α ∧ β).

If ¬β ∈ Cn(Z ∪{¬(α ∧ β)}), thenZ ⊩¬(α ∧ β) →¬β. It followsthat Z ⊩ β → α from thefact (¬(α ∧ β) →¬β) ≡ β → α. Sinceβ → α ∈ Z, we thus havethat Cn(Z ∪{¬(α ∧ β)}) = Cn(Z ∪{¬β}). Thismeans that Z ∈ S(K,β)according to the definition of saturatable set. Now let X be any element ofS(K,β). According to the upper bound property, there is some X^′such that X ⊆ X^′∈ K⊥β. SinceK⊥β ⊆ K⊥(α ∧ β), thus we havethat X^′∈ K⊥(α ∧ β). Further, weknow that for any Y ∈ K⊥α,Y ∈ S(K,α). Thus weknow that X^′∈ S(K,α ∧ β).According to the property of weak monotonicity, it follows fromX ⊆ X^′thatX ≤ X^′. Thenfrom X^′∈ S(K,α ∧ β)andZ ∈ γ(S(K,α ∧ β))we have thatX^′≤ Z. By transitivity, itimplies that X ≤ Z. Since X isan arbitrary element of S(K,β)and Z ∈ S(K,β), this impliesthat Z ∈ γ(S(K,α)). Andthus K ÷ α ⊆ Z. Sincex ∈ K ÷ α, it implies thatx ∈ Z, which contradictsthe fact that x∉Z(which was derived from the main assumption, namely thatx∉K ÷ (α ∧ β)).

Therefore, we can conclude x ∈ Z,which establishes that K ÷ β ⊆ K ÷ (α ∧ β).□

Lemma 19

Let÷be a relation-based saturatable contraction over K. Then it satisfies partial antitony.

Proof

Suppose that x ∈ K ÷ α and x ∈ Cn(α). We needto show that x ∈ K ÷ (α ∧ β).Consider the following cases.

Case 1::

If α∉K or β∉K,then it follows that α ∧ β∉K.Then by vacuity, we have that K ÷ (α ∧ β) = K.According to inclusion, we have that x ∈ K ÷ α ⊆ K = K ÷ (α ∧ β)as required.

Case 2::

If α ∈ K,β ∈ K,and ⊩ α ∧ β,then again by vacuity, we have that K ÷ (α ∧ β) = K.Similarly, it follows that x ∈ K ÷ α ⊆ K ÷ (α ∧ β)by inclusion.

Case 3::

Now consider the case that α,β ∈ K ∖ Cn(∅).Assume that x∉K ÷ (α ∧ β).It follows that there is some Z such thatx∉Z ∈ γ(S(K,α ∧ β)).According to the definition of saturatable set, we have thatCn(Z ∪{¬(α ∧ β)})is maximally consistent in L. Hence, either α or ¬α belongs to Cn(Z ∪{¬(α ∧ β)}).

If α ∈ Cn(Z ∪{¬(α ∧ β)}), thenZ ⊩¬(α ∧ β) → α. This followsthat Z ⊩ α, since(¬(α ∧ β) → α) ≡ α. However,since x ∈ Cn{α}, itfollows that x ∈ Z,which contradicts the assumption.

If ¬α ∈ Cn(Z ∪{¬(α ∧ β)}), thenZ ⊩¬(α ∧ β) →¬α. It followsthat Z ⊩ α → β from thefact (¬(α ∧ β) →¬α) ≡ α → β. Sinceα → β ∈ Z, we thus havethat Cn(Z ∪{¬(α ∧ β)}) = Cn(Z ∪{¬α}). Thismeans that Z ∈ S(K,α)according to the definition of saturatable set. Now let X be any element ofS(K,α). According to the upperbound property, there is some X^′such that X ⊆ X^′∈ K⊥α. SinceK⊥α ⊆ K⊥(α ∧ β), thus we have thatX^′∈ K⊥(α ∧ β). Further, we know thatfor any Y ∈ K⊥α it follows thatY ∈ S(K,α), which implies thatX^′∈ S(K,α ∧ β). According to the propertyof weak monotonicity, from X ⊆ X^′we have that X ≤ X^′.It follows from X^′∈ S(K,α ∧ β)and Z ∈ γ(S(K,α ∧ β))thatX^′≤ Z. By transitivity, wehave that X ≤ Z. Since X isan arbitrary element of S(K,α)and Z ∈ S(K,α), itimplies that Z ∈ γ(S(K,α)),and thus K ÷ α ⊆ Z.Since x ∈ K ÷ α, itimplies that x ∈ Z,which again contradicts the assumption.

Therefore, we can concludex ∈ Z, which establishes that(K ÷ α) ∩ Cn(α) ⊆ K ÷ (α ∧ β).□

Lemma 20

Let K be a theory and let÷be a contraction operator for K that satisfies closure, inclusion, vacuity, extensionality, andconjunctive inclusion. Then it satisfies conjunctive overlap and conjunctive reduction if andonly if it satisfies conjunctive factoring.

Proof

(⇐) Conjunctive overlap follows directly from conjunctive factoring. Itremains to be shown that conjunctive reduction holds. Assume thatα ∈ K ÷ (α ∧ β).In the limiting case when ⊩ α, conjunctive reduction trivially holds. Now consider the case when$\nvdash \alpha$.Then vacuity yields α∉K ÷ α.Since α ∈ K ÷ (α ∧ β),it is impossible that K ÷ (α ∧ β) = K ÷ α and K ÷ (α ∧ β) = (K ÷ α) ∩ (K ÷ β).By ruling out these two possibilities, we can conclude from conjunctive factoring thatK ÷ (α ∧ β) = K ÷ β.Therefore, conjunctive reduction holds as well.

(⇒)Consider K ÷ (α ∧ β).There are three cases that are mutually exclusive and exhaustive: eitherα ∈ K ÷ (α ∧ β)and β∉K ÷ (α ∧ β),or α∉K ÷ (α ∧ β)and β ∈ K ÷ (α ∧ β),or α∉K ÷ (α ∧ β)and β∉K ÷ (α ∧ β).We will show that in the first case K ÷ β = K ÷ (α ∧ β),in the second case K ÷ α = K ÷ (α ∧ β)and in the third case K ÷ α ∩ K ÷ β = K ÷ (α ∧ β).

Consider the first case: α ∈ K ÷ (α ∧ β)and β∉K ÷ (α ∧ β).Then by conjunctive inclusion we have that K ÷ (α ∧ β) ⊆ K ÷ β.On the other hand since α ∈ K ÷ (α ∧ β),we have by conjunctive reduction that K ÷ β ⊆ K ÷ (α ∧ β).

The case α∉K ÷ (α ∧ β)and β ∈ K ÷ (α ∧ β)is analogous, yielding the desired K ÷ α = K ÷ (α ∧ β).

Finally in the third case by two applications of conjunctive inclusion we have thatK ÷ (α ∧ β) ⊆ (K ÷ α) ∩ (K ÷ β). Conjunctive overlap provides the converse inclusion, proving the proposition.□

Proposition 23

Let K be a theory and letγbe a selection function for K. Then:

• (i) The completion functionγ^∗is a selection function for K;

• (ii) γ(S(K,α)) ⊆ γ^∗(S(K,α))for allα;

• (iii) $\bigcap \gamma (S(K,\alpha ))=\bigcap \gamma ^{*}(S(K,\alpha ))$ for all α .

Proof

• (i) It is easy to verified that γ^∗satisfies the two conditions of the definition of selection function.

• (ii) If S(K,α)is empty, then we have that γ(S(K,α)) = γ^∗(S(K,α)) = {K},which follows that γ(S(K,α)) ⊆ γ^∗(S(K,α))as desired. If S(K,α)is nonempty, then it holds for every X ∈ S(K,α) that $\bigcap \gamma (S(K,\alpha ))\subseteq X$.According to the definition of γ^∗we have that X ∈ γ^∗(S(K,α)).Therefore, we can conclude that γ(S(K,α)) ⊆ γ^∗(S(K,α))for all α.

• (iii) First, if S(K,α)is empty, then similarly we have that γ(S(K,α)) = γ^∗(S(K,α)) = {K},which implies that $\bigcap \gamma (S(K,\alpha ))=\bigcap \gamma ^{*}(S(K,\alpha ))$.Second, if S(K,α)is nonempty. From the definition of γ^∗we have that $\bigcap \gamma (S(K,\alpha ))\subseteq X$for every X ∈ γ^∗(S(K,α)).It shows that $\bigcap \gamma (S(K,\alpha ))\subseteq \bigcap \gamma ^{*}(S(K,\alpha ))$.Moreover, by (ii) of the present proof, we know thatγ(S(K,α)) ⊆ γ^∗(S(K,α)).This implies that $\bigcap \gamma ^{*}(S(K,\alpha ))\subseteq \bigcap \gamma (S(K,\alpha ))$.We can therefore conclude that $\bigcap \gamma (S(K,\alpha ))=\bigcap \gamma ^{*}(S(K,\alpha ))$.

□

Theorem 24

Let K be a theory and let÷be an operator for K that satisfies closure, inclusion, vacuity, success, extensionality,conjunctive inclusion, partial antitony and conjunctive factoring. Then÷is a relation-based saturatable contraction determined by a selection functionγwhichsatisfies the following conditions:

• (i) γsatisfies the marking-off identity, i.e.,γ(S(K,α)) = {X ∈ S(K,α)∣Y ≤ X, for all Y ∈ S(K,α)},for allα ∈ K ∖ Cn(∅);

• (ii) The relation≤is transitive;

• (iii) The relation≤satisfies the weak monotonicity, i.e., ifY ⊂ X,thenY ≤ X.

Proof

Let K be any theory, and ÷a Levi-contraction function over K, determined by a selection functionγ. We have toshow that if ÷satisfies in addition conjunctive inclusion, partial antitony, and conjunctive factoring, then there is a transitive and weakly monotonic relation≤suchthat γ satisfies the marking-off identity with respect to this relation. It is easy to verify that the selectionfunction γ i question is complete. So let us define explicitly the relation≤over thedomain KΔL = {X∣X ∈ S(K,α) for some α ∈ K ∖ Cn(∅)}suchthat for all X,Y ∈ KΔL,Y ≤ X if andonly if one of the following conditions holds

• (1) Y ⊆ X;

• (2) There is α ∈ K ∖ Cn(∅)such that Y ∈ S(K,α)AND There is some α ∈ K ∖ Cn(∅)[(X ∈ S(K,α),and K ÷ α ⊆ X),AND for all β ∈ K ∖ Cn(∅)(if X ⊆ X^′∈ K⊥(β ∧ α)and Y ⊆ Y^′∈ K⊥(β ∧ α),and K ÷ β ⊆ Y^′,then (if K ÷ (α ∧ β)≠K ÷ α,then K ÷ (α ∧ β) = K ÷ α ∩ K ÷ β)and K ÷ β ⊆ X^′)].

We need to show that the relation defined in this way satisfies the three conditions given in theproposition.

• (i) We first show that γ satisfies the marking-off identity. Let α ∈ K ∖ Cn(∅).Suppose that X ∈ γ(S(K,α)) ⊆ S(K,α).We need to show that X ∈{X ∈ S(K,α)∣Y ≤ X, for all Y ∈ S(K,α)}.It suffices to show that Y ≤ X for any Y ∈ S(K,α).

  Then it is clear that the first part of condition (2) is already satisfied. Letβ ∈ K ∖ Cn(∅).And suppose that K ÷ β ⊆ Y^′We need to show that K ÷ β ⊆ X^′and, if K ÷ α ∧ β≠K ÷ α,then K ÷ (α ∧ β) = K ÷ α ∩ K ÷ β.

  Let us focus first on K ÷ (α ∧ β).We know by conjunctive covering that eitherK ÷ (α ∧ β) ⊆ K ÷ β or K ÷ (α ∧ β) ⊆ K ÷ α.Assume that K ÷ (α ∧ β) ⊆ K ÷ β.Since it is assumed K ÷ β ⊆ Y^′,we have K ÷ (α ∧ β) ⊆ K ÷ β ⊆ Y^′∈ K⊥α,which implies that α∉K ÷ (α ∧ β).Thus by conjunctive inclusion we have thatK ÷ (α ∧ β) ⊆ K ÷ α.Therefore in both cases we have that K ÷ (α ∧ β)⊆ K ÷ α.

  By conjunctive factoring K ÷ (α ∧ β)is either equal to K ÷ α,to K ÷ β or to the intersection of these two sets. Suppose thatK ÷ (α ∧ β)≠K ÷ α.If K ÷ (α ∧ β) = K ÷ β,then it implies that K ÷ (α ∧ β) = K ÷ α ∩ K ÷ β,for we already have that K ÷ (α ∧ β) ⊆ K ÷ α.Hence it holds that K ÷ (α ∧ β) = K ÷ α ∩ K ÷ β.This proves that if K ÷ (α ∧ β)≠K ÷ α,then K ÷ (α ∧ β) = K ÷ α ∩ K ÷ β.

  We need to prove now that K ÷ β ⊆ X^′.Assume that δ ∈ K ÷ β.Consider the following instance of partial antitony:

  $$(K\div\beta)\cap Cn(\beta)\subseteq K\div(\alpha\wedge\beta). $$

  Since we assumed that δ ∈ K ÷ β we have as well that δ ∨ β ∨ α ∈ K ÷ β,and since δ ∨ β ∨ α ∈ Cn(β)we havethat δ ∨ β ∨ α ∈ K ÷ (α ∧ β). Moreoversince we have that K ÷ (α ∧ β) ⊆ K ÷ α ⊆ X ⊆ X^′,we also have that δ ∨ β ∨ α ∈ X^′.

  Note that X^′∈ K⊥(β ∧ α)and δ ∈ K. It thusimplies that X^′∪{α,β}⊩ δ. Sowe have that ¬β → (¬α → δ) ∈ X^′and β → (α → δ) ∈ X^′, whichentail that δ ∈ X^′. Itfollows that K ÷ β ⊆ X^′.This completes the proof by establishing the desired result thatY ≤ X.

  For the converse, suppose that X∉γ(S(K,α))for some α ∈ K ∖ Cn(∅). We needto show that X∉{X ∈ S(K,α)∣Y ≤ X, for all X ∈ S(K,α)}. Notethat if X∉S(K,α), then ittrivially follows that X∉{X ∈ S(K,α)∣Y ≤ X, for all X ∈ S(K,α)}.Thus, suppose that X ∈ S(K,α).To show that X∉{X ∈ S(K,α)∣Y ≤ X, for all X ∈ S(K,α)}, itsuffices to find some Y ∈ S(K,α) with $Y\nleq X$. SinceX ∈ S(K,α), it means thatS(K,α)is nonempty, whichfollows that γ(S(K,α))is nonempty.Thus let Y ∈ γ(S(K,α)). Then we havethat $K\div \alpha =\bigcap \gamma (S(K,\alpha ))\subseteq Y$. On the other hand,since X∉γ(S(K,α)), we can concludefrom the property of γ that $\bigcap \gamma (S(K,\alpha ))\nsubseteq X$. Thus we have$K\div \alpha \nsubseteq X$. From these, wecan conclude that $Y\nsubseteq X$,which establishes that condition (1) does not hold. And note thatX,Y ∈ S(K,α),K ÷ α ⊆ Y, but$K\div \alpha \nsubseteq X$.

  We have to check that condition (2) is not satisfied either. Notice that the negation ofcondition (2) is given as follows:

  ¬Thereis α ∈ K ∖ Cn(∅)suchthat Y ∈ S(K,α)ORFor all α ∈ K ∖ Cn(∅)[if (X,Y ∈ S(K,α), andK ÷ α ⊆ X), THENthere is β ∈ K ∖ Cn(∅)(X ⊆ X^′∈ K⊥(β ∧ α)andY ⊆ Y^′∈ K⊥(β ∧ α), andK ÷ β ⊆ Y^′, andeither ¬(if K ÷ (α ∧ β)≠K ÷ α,then K ÷ (α ∧ β) = K ÷ α ∩ K ÷ β)or K ÷ β⫅̸X^′)].

  We need to find an adequate β in K in order to prove the truth of the second disjunct. Can we argue that such aβ exists in K? The answer is yes if the belief sets used in the theory are finitely axiomatizable in the sense that a formulaψ represents a beliefset K if and only if K = {ϕ : ψ ⊩ ϕ}.If we assume that all belief sets are representable by a formulain the language we can argue as follows to identify the neededβ in K:

  Let w be the maximal and consistent belief set such thatCn(Y ∪{¬α}) = w. Let¬ψ represent w.Then clearly ψ ∈ K. Setβ = ψ. Clearly also in thiscase K ÷ β ⊆ Y^′. Assume now bycontradiction that K ÷ β ⊆ X^′.Let [K ÷ β]the set of worlds that correspond to the theoryK ÷ β. It is clear thatw is the only ¬α world in [K ÷ β]. Nownotice that since X^′≠Y^′we have that [Y^′]= {w}∪ [K]and[Y^′]={w∗}∪ [K]where w andw ∗should be distinct¬α worlds. But from ourassumption we have that [X^′] ⊆ [K ÷ β],which entails that w ∗is in [K ÷ β].But this is impossible because we already saw that[K ÷ β]should containa unique ¬α world, namely w.

  In addition we also have that X^′,Y^′∈ K⊥(β ∧ α).Notice that X,Y ∈ S(K,α).Therefore X^′,Y^′∈ K⊥α,and since K⊥α ⊆ K⊥(β ∧ α)we are done.

• (ii) Next we are going to show that ≤is transitive. Let X,Y,Z ∈ KΔL.Suppose that Z ≤ Y and Y ≤ X. We needto show that Z ≤ X.Let us consider the following cases.

Case 1::

Both Z ≤ Y and Y ≤ X hold due to condition (1). In this case, we have thatZ ⊆ Y and Y ⊆ X.Thus according to the definition, we have thatZ ≤ X as required.

Case 2::

Z ≤ Y holds because of condition (1), and Y ≤ X holds due to condition (2). So, we have that:

(2’):

There is α ∈ K ∖ Cn(∅)such that Y ∈ S(K,α)AND There is some α^′∈ K ∖ Cn(∅)[(X ∈ S(K,α^′),and K ÷ α^′⊆ X),AND for all β ∈ K ∖ Cn(∅)(if X ⊆ X^′∈ K⊥(β ∧ α^′)and Y ⊆ Y^′∈ K⊥(β ∧ α^′),and K ÷ β ⊆ Y^′,then (if K ÷ (α^′∧ β)≠K ÷ α^′,then K ÷ (α^′∧ β) = K ÷ α^′∩ K ÷ β)and K ÷ β ⊆ X^′)].

And we need to prove that:

(2”):

There is α ∈ K ∖ Cn(∅)such that Z ∈ S(K,α)AND There is some α^′∈ K ∖ Cn(∅)[(X ∈ S(K,α^′),and K ÷ α^′⊆ X),AND for all β ∈ K ∖ Cn(∅)(if X ⊆ X^′∈ K⊥(β ∧ α^′)and Z ⊆ Z^′∈ K⊥(β ∧ α^′),and K ÷ β ⊆ Z^′,then (if K ÷ (α^′∧ β)≠K ÷ α^′,then K ÷ (α^′∧ β) = K ÷ α^′∩ K ÷ β)and K ÷ β ⊆ X^′)].

First since Z ≤ Y holds becauseof condition (1), we have that Z ⊆ Y.And note that Z,Y ∈ KΔL. It thusmust be the case that Z^′ = Y^′and Z^′,Y^′∈ K⊥α for someα ∈ K ∖ Cn(∅). Consider thisparticular α. It thusfollows from Z^′,Y^′∈ K⊥α that Z,Y ∈ S(K,α)for thisparticular α.So the first existential clause is satisfied. The second existential clause is also satisfied given thatY ≤ X holds due to condition (2). And the universal clause can be easily established forZ^′ = Y^′and thefact that Y ≤ X holds due to condition (2).

We are first going to show that K ÷ β ⊆ X^′.Let δ ∈ K ÷ β. First itfollows from X^′∈ K⊥(β ∧ α^′),Z^′∈ K⊥(β ∧ α^′), andY^′∈ K⊥α thatX^′,Y^′,Z^′∈ K⊥(α ∧ β ∧ α^′). SinceY ≤ X holds because of condition(2), we can infer that K ÷ (α ∧ β) ⊆ X^′by taking (α ∧ β)as theinstance of β in (2’).It follows from δ ∈ K ÷ β that δ ∨ β ∨ α^′∈ K ÷ β. Andclearly δ ∨ β ∨ α^′∈ Cn(β).Now consider the following instance of partial antitony:

$$(K\div\beta)\cap Cn(\beta)\subseteq K\div(\alpha\wedge\beta). $$

Then it implies that δ ∨ β ∨ α^′∈ K ÷ (α ∧ β) ⊆ X^′.Moreover, since we assumed that X^′∈ K⊥(β ∧ α^′)and δ ∈ K ÷ β ⊆ K, we have aswell that X^′∪{α^′,β}⊩ δ. So theseimply that δ ∈ X^′. Thiscompletes the proof of K ÷ β ⊆ X^′.

Case 3::

Z ≤ Y holds because of condition (2), and Y ≤ X holds due to condition (1). This case is similar to the previous case.

Case 4::

Both Z ≤ Y and Y ≤ X hold because condition (2). Unpacking definitions we have:

(2-Z-Y):

There is α ∈ K ∖ Cn(∅)such that Z ∈ S(K,α)AND There is some α^′∈ K ∖ Cn(∅)[(Y ∈ S(K,α^′),and K ÷ α^′⊆ Y ),AND for all β ∈ K ∖ Cn(∅)(if Z ⊆ Z^′∈ K⊥(β ∧ α^′)and Y ⊆ Y^′∈ K⊥(β ∧ α^′),and K ÷ β ⊆ Z^′,then (if K ÷ (α^′∧ β)≠K ÷ α^′,then K ÷ (α^′∧ β) = K ÷ α^′∩ K ÷ β)and K ÷ β ⊆ Y^′)].

On the other hand we also have:

(2-Y-X):

There is α^′∈ K ∖ Cn(∅)such that Y ∈ S(K,α^′)AND There is some α^″∈ K ∖ Cn(∅)[(X ∈ S(K,α^″),and K ÷ α^″⊆ X),AND for all β ∈ K ∖ Cn(∅)(if X ⊆ X^′∈ K⊥(β ∧ α^″)and Y ⊆ Y^′∈ K⊥(β ∧ α^″),and K ÷ β ⊆ Y^′,then (if K ÷ α^″∧ β≠K ÷ α^″,then K ÷ (α^″∧ β) = K ÷ α^″∩ K ÷ β)and K ÷ β ⊆ X^′)].

And we need to prove:

(2-Z-X):

There is α ∈ K ∖ Cn(∅)such that Z ∈ S(K,α)AND There is some α^″∈ K ∖ Cn(∅)[(X ∈ S(K,α^″),and K ÷ α^″⊆ X),AND for all β ∈ K ∖ Cn(∅)(if X ⊆ X^′∈ K⊥(β ∧ α^″)and Z ⊆ Z^′∈ K⊥(β ∧ α^″),and K ÷ β ⊆ Z^′,then (if K ÷ (α^″∧ β)≠K ÷ α^″,then K ÷ (α^″∧ β) = K ÷ α^″∩ K ÷ β)and K ÷ β ⊆ X^′)].

It is clear that the first existential clause of (2-Z-X) is given by (2-Z-Y) while the second isgiven by (2-Y-X). We need to prove the universally quantified clause. Assume thatX ⊆ X^′∈ K⊥β ∧ α^″andZ ⊆ Z^′∈ K⊥β ∧ α^″, andK ÷ β ⊆ Z^′. We need toprove that K ÷ β ⊆ X^′and (if K ÷ α^″∧ β≠K ÷ α^″, thenK ÷ (α^″∧ β) = K ÷ α^″∩ K ÷ β). We will prove fist thatK ÷ β ⊆ X^′, and then we will use thisresult to prove that (if K ÷ α^″∧ β≠K ÷ α^″,then K ÷ (α^″∧ β) = K ÷ α^″∩ K ÷ β).

By the property of reminder sets establishing thatK⊥(β ∧ α^′∧ α^″) = K⊥(β ∧ α^″) ∪ K⊥α^′we havethat Z^′,X^′,Y^′∈ K⊥(β ∧ α^′∧ α^″). Infact, Y ∈ S(K,α^′), andtherefore Y^′∈ K⊥α^′and Z^′,X^′are in K⊥(β ∧ α^″).

By covering, either K ÷ (β ∧ α^′∧ α^″) ⊆ K ÷ β orK ÷ (β ∧ α^′∧ α^″) ⊆ K ÷ (α^′∧ α^″). In the first case we have thatK ÷ (β ∧ α^′∧ α^″) ⊆ Z^′. So, by taking appropriateinstances of β in (2-Z-Y)and (2-Y-X) we have that K ÷ (β ∧ α^′∧ α^″) ⊆ X^′.

On the other hand if we consider the caseK ÷ (β ∧ α^′∧ α^″) ⊆ K ÷ (α^′∧ α^″), we proceed by cases. Byconjunctive covering either K ÷ (α^′∧ α^″) = K ÷ α^′orK ÷ (α^′∧ α^″) ⊆ K ÷ α^″. In the first case we have thatK ÷ (β ∧ α^′∧ α^″) ⊆ K ÷ α^′⊆ Y^′. Then we can fire (2-Y-X)and we get K ÷ (β ∧ α^′∧ α^″) ⊆ X^′. In the secondcase we have that K ÷ (β ∧ α^′∧ α^″) ⊆ K ÷ α^″⊆ X^′. So, in allpossible cases we have that K ÷ (β ∧ α^′∧ α^″) ⊆ X^′.

We need to prove that K ÷ β ⊆ X^′.Assume that δ ∈ K ÷ β.Consider the following instance of partial antitony:

$$(K\div\beta)\cap Cn(\beta)\subseteq K\div(\beta\wedge\alpha^{\prime}\wedge\alpha^{\prime\prime}). $$

Since we assumed that δ ∈ K ÷ β we have as well that (β ∨ α^′∨ α^″∨ δ) ∈ K ÷ β,and since (β ∨ α^′∨ α^″∨ δ) ∈ Cn(β)wehave that (β ∨ α^′∨ α^″∨ δ) ∈ K ÷ (β ∧ α^′∧ α^″) ⊆ X^′.

On the other hand since X ∈ K⊥(α^″∧ β)and δ ∈ K wehave that X^′∪{α^″,β}⊩ δ from which (by monotonicity of the notion of consequence) we have:X^′∪{α^″,α^′,β}⊩ δ. So, clearlyδ ∈ X^′. This completesthe proof of K ÷ β ⊆ X^′.

Now we need to prove that (if K ÷ α^″∧ β≠K ÷ α^″,then K ÷ (α^″∧ β) = K ÷ α^″∩ K ÷ β).Assume that antecedent. By conjunctive covering eitherK ÷ (α^″∧ β) ⊆ K ÷ β orK ÷ (α^″∧ β) ⊆ K ÷ α^″. Let’s start with the firstdisjunct. Since we have that K ÷ (α^″∧ β) ⊆ K ÷ β and we proved that K ÷ β ⊆ X^′⊆ K⊥α^″, we knowthat α^″∉K ÷ (α^″∧ β). Therefore by conjunctive inclusionK ÷ (α^″∧ β) ⊆ K ÷ α^″. In addition byconjunctive overlap we have that K ÷ α^″∩ K ÷ β ⊆ K ÷ (α^″∧ β).Therefore we have that K ÷ α^″∩ K ÷ β = K ÷ (α^″∧ β) as desired.

Let’s consider now the second disjunct K ÷ (α^″∧ β) ⊆ K ÷ α^″.Since we assumed that K ÷ (α^″∧ β)≠K ÷ α^″,we know that K ÷ α^″⫅̸K ÷ (α^″∧ β).Therefore by conjunctive reduction we have thatβ∉K ÷ (α^″∧ β), and this by conjunctive inclusion yields that K ÷ (α^″∧ β) ⊆ K ÷ β.Now by invoking conjunctive overlap again, we have thatK ÷ α^″∩ K ÷ β = K ÷ (α^″∧ β)asdesired. This completes the general proof.

• (iii) We need to show that ≤satisfies the weak monotonicity. Let X,Y ∈ S(K,α)for some α ∈ K ∖ Cn(∅).Assume that Y ⊂ X.According to condition (1), it directly follows fromY ⊂ X that Y ≤ X as desired.

□