Abstract
A completely regular semigroup is a (disjoint) union of its (maximal) subgroups. We consider it here with the unary operation of inversion within its maximal subgroups. Their totality \(\mathcal {C}\mathcal {R}\) forms a variety whose lattice of subvarieties is denoted by \(\mathcal {L}(\mathcal {C}\mathcal {R})\). On it, one defines the relations \(\mathbf {B}^\wedge \) and \(\mathbf {B}^\vee \) by
respectively, where \(\mathcal {B}\) denotes the variety of all bands. This is a study of the interplay between the \(\cap \)-subsemilatice \(\triangle \) of \(\mathcal {L}(\mathcal {C}\mathcal {R})\) of upper ends of \(\mathbf {B}^\wedge \)-classes and their \(\mathbf {B}^\vee \)-classes. The main tool is the concept of a ladder and their \(\mathbf {B}^\vee \)-classes, an indispensable part of the important Polák’s theorem providing a construction for the join of varieties of completely regular semigroups. The paper includes the tables of ladders of the upper ends of most \(\mathbf {B}^\wedge \)-classes. Canonical varieties consist of two ascending countably infinite chains which generate most of the upper ends of \(\mathbf {B}^\wedge \)-classes.


Similar content being viewed by others
References
P.R. Jones, Mal’cev products of varieties of completely regular semigroups. J. Aust. Math. Soc. A 42, 227–246 (1987)
J. Kad̆ourek, On the word problem for bands of groups and free objects in some other varieties of completely regular semigroups. Semigroup Forum 38, 1–55 (1989)
F. Pastijn, The lattice of completely regular semigroup varieties. J. Aust. Math. Soc. A 49, 24–42 (1990)
M. Petrich, Some relations on the lattice of varieties of completely regular semigroups. Bol. Unione Mat. Ital. B 5, 265–278 (2002)
M. Petrich, Canonical varieties of completely regular semigroups. J. Aust. Math. Soc. 83, 87–104 (2007)
M. Petrich, Varieties of completely regular semigroups related to canonical varieties. Semigroup Forum 90, 53–99 (2015)
M. Petrich, New operators for varieties of completely regular semigroups. Semigroup Forum 91, 415–449 (2015)
M. Petrich, An equation for operators on varieties of completely regular semigroups. Acta Math. Hung. 146, 341–375 (2015)
M. Petrich, Certain relations on a lattice of varieties of completely regular semigroups. Commun. Algebra 43, 4080–4096 (2015)
M. Petrich, N.R. Reilly, Operators related to \(E\)-disjunctive and fundamental completely regular semigroups. J. Algebra 134, 1–27 (1990)
M. Petrich, N.R. Reilly, Operators related to idempotent generated and monoid completely regular semigroups. J. Aust. Math. Soc. A 49, 1–23 (1990)
M. Petrich, N.R. Reilly, Completely Regular Semigroups (Wiley, New York, 1999)
L. Polák, On varieties of completely regular semigroups I. Semigroup Forum 32, 97–123 (1985)
L. Polák, On varieties of completely regular semigroups II. Semigroup Forum 36, 253–284 (1987)
V.V. Rasin, On the varieties of completely regular semigroups. Semigroup Forum 23, 201–220 (1981)
N.R. Reilly, S. Zhang, Decomposition of the lattice of pseudovarieties of finite semigroups induced by bands. Algebra Univers. 44, 217–239 (2000)
P.G. Trotter, Subdirect decompositions of the lattice of varieties of completely regular semigroups. Bull. Aust. Math. Soc. 39, 343–351 (1989)
Acknowledgements
Assistance of Antonio M. Cegarra is deeply appreciated.
Author information
Authors and Affiliations
Corresponding author
Appendix: Tables of ladders of varieties in \(\triangle \)
Appendix: Tables of ladders of varieties in \(\triangle \)
These tables have been referred to in the text. In general they give great help in treating the varieties in \(\triangle \). We have classified the tables in five types I–V, and in each type, the values of subscripts are divided into those of even and odd parity. The last criterium for distinction is the number of rows containing entries greater that \(\mathcal {J}\). We listed the ladders for the lowest subscript separately in order to indicate how to start.
- Type I:
-
On the upper half of the first page of the tables are listed ladders of \(\mathcal {H}_n\), for n even and odd, and their duals for \(\overline{\mathcal {H}}_n\).
- Type II:
-
The lower part of the first page contains the same information for \(\mathcal {I}_n\) and \(\overline{\mathcal {I}}_n\).
- Type III:
-
The upper part of the second page contains the information for \(\mathcal {H}_n \cap \overline{\mathcal {H}}_n\) and \(\mathcal {I}_n \cap \overline{\mathcal {I}}_n\).
- Type IV:
-
The lower part of the second page contains the information for \(\mathcal {H}_n \cap \overline{\mathcal {I}}_n\) and \(\overline{\mathcal {H}}_n \cap {\mathcal {I}}_n\).
- Type V:
-
The third page contains ladders for \(\mathcal {H}_{n+1} \cap \overline{\mathcal {I}}_n\) and \(\overline{\mathcal {H}}_{n+1} \cap {\mathcal {I}}_n\).
In the computation of these ladders we have a number of helpful results that make things move quickly. Here are some of them.
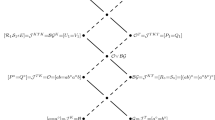
Fact 3.2 which asserts that for any \(\mathcal {V}\in \triangle \) such that \(\mathcal {V}\supseteq \mathcal {R}e\mathcal {B}\), we have \(\mathcal {V}=\mathcal {V}_K\). This means that in Fig. 1, all varieties higher or equal to \(\mathcal {R}=\mathcal {I}_3\cap \overline{\mathcal {I}}_3\) are least members of their \(\mathbf {K}\)-classes. In the complement of this set in \(\triangle \), only \(\mathcal {G}\) and \(\mathcal {C}\mathcal {S}\) are least in their \(\mathbf {K}\)-classes; the greatest members of their \(\mathbf {K}\)-classes are \(\mathcal {O}\) and \(\mathcal {O}^L\), respectively. Hence no two different members of \(\triangle \) above \(\mathcal {R}\) are \(\mathbf {K}\)-related.
Fact 3.3 gives \(\mathbf {T}_{\,l}\)- and \(\mathbf {T}_{\,r}\)-classes of all proper members of \(\triangle \), in a simple explicit way. We have seen in Sect. 6 that for varieties in \(\triangle \), the ladder of the meet is the meet of the ladders computed by entries. Finally all entries of \(lad\,\mathcal {B}\) are equal to \(\mathcal {J}\), which is a great convenience. With these helpful hints, it is left to the reader to compute the ladders of all key cases. We omit \(T^*\) in the tables.
The ladders in Tables 1 and 2 follow the same pattern. Below we prove correctness of Table 1 for \(\mathcal {H}_n\) and \(\overline{\mathcal {H}}_n\) by induction on n. Table 2 for \({\mathcal {I}}_n\) and \(\overline{\mathcal {I}}_n\) follows the same pattern. Tables 3, 4 and 5 treat meets of pairs in Tables 1 and 2. The ladder operation is in general not compatible with meet. But here Corollary 4.5 comes to help since we are dealing with canonical varieties, and thus may form meets of ladders (defined componentwise).
For \(\mathcal {V}_K\), we have Fact 2.7 for \({\mathcal {H}}_2\), \({\mathcal {H}}_3\) and their duals, for the remaining \({\mathcal {H}}_n\) and \(\overline{\mathcal {H}}_n\), Fact 3.2 asserts that \(({\mathcal {H}}_n)_K=\mathcal {H}_n\) and \((\overline{\mathcal {H}}_n)_K=\overline{\mathcal {H}}_n\), where we can use [6, Theorem 10.2] to conclude the \({\mathcal {H}}_n^T={\mathcal {H}}_n\) and \(\overline{\mathcal {H}}_n^T=\overline{\mathcal {H}}_n\).
Example 6.8
Ladders of \({\mathcal {H}}_n\) and \(\overline{\mathcal {H}}_n\). We omit \(T^*\) throughout. The proof is by induction on n starting with \({\mathcal {H}}_3\) and \(\overline{\mathcal {H}}_3\). The ladders of \(\mathcal {H}_2\), \(\overline{\mathcal {H}}_2\), \(\mathcal {H}_3\), \(\overline{\mathcal {H}}_3\) can be constructed by using Fact 2.3.
Note that the passage from \(lad\ \mathcal {V}\) to \(lad\ \overline{\mathcal {V}}\) consists of exchanging the columns of the former and exchanging \(L^*\) and \(R^*\) (but the barred varieties must be restricted to the second column).
The first step of the induction process consists of ladders, again constructed by using Fact 2.3,

For the induction step, we state only the case of n being even; the odd case is treated analogously. Hence we assume validity of

and must show the validity of

It remains to check that
- (a):
-
the part of C from \(\overline{\mathcal {H}}_{n}\) down coincides with B,
- (b):
-
the part of D from \({\mathcal {H}}_{n}\) down coincides with A,
- (c):
-
in C:
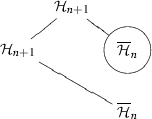 (d) in D:
(d) in D: 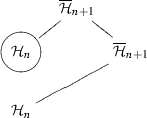
are both correct.
All this checks out and the induction procedure is complete.
It remains to construct the ladder of \(\mathcal {C}\mathcal {R}\).
Trivially \(\mathcal {C}\mathcal {R}=\mathcal {C}\mathcal {R}^T\supseteq \mathcal {R}e\mathcal {B}\), which by Fact 2.1 yields \(\mathcal {C}\mathcal {R}_K=\mathcal {C}\mathcal {R}\). Again trivially \(\mathcal {C}\mathcal {R}^K=\mathcal {C}\mathcal {R}\) so that by Fact 2.5 (i), we get \(\mathcal {C}\mathcal {R}=\mathcal {C}\mathcal {R}_{T_l}=\mathcal {C}\mathcal {R}_{T_r}\). Therefore the ladder of \(\mathcal {C}\mathcal {R}\) has the form

The above tables of ladders coincide with the image of \(\chi \) in Theorem 4.1. As we have seen, this theorem needs an irreducible minimum of about page and half of concepts and notation. As contrasted to this, Proposition 7.4 needs only the concept of network and its evaluation which needs about 2/3 of a page. And is easy to understand and remember.
If we want networks instead of ladders for the canonical varieties and their meets, in the tables of ladders, we can reconvert \(L^*\), \(T^*\), \(R^*\) back into \(\mathcal {L}\mathcal {N}\mathcal {B}\), \(\mathcal {S}\), \(\mathcal {R}\mathcal {N}\mathcal {B}\), respectively.
How do these results fit in the scheme of studying the structure of \(\mathcal {L}(\mathcal {C}\mathcal {R})\)? The concepts of kernel, (left and right) trace, local, and core relations have enlarged considerably the arsenal of “familiar” varieties, defined and studied. Hopefully the relations \(\mathbf {B}^{\wedge }\) and \(\mathbf {B}^{\vee }\) will have the same impact. They are new, for they were introduced, together with \(\mathbf {G}^{\wedge }\), \(\mathbf {G}^{\vee }\), \(\mathbf {CS}^\wedge \), \(\mathbf {CS}^\vee \) in [7] only recently. Most of the relevant results concern locally orthodox varieties; for other varieties they present considerable difficulties. For the practical manipulation of the resulting operators induced on \(\mathcal {L}(\mathcal {C}\mathcal {R})\), seminal role is played by their mutual relationship, in particular the determination of which pairs commute. Another factor in the considerations is the satisfaction of the equation of the form \((\mathcal {V}^A)_B=\mathcal {V}^A\) for certain operators \(\mathcal {V}\mapsto \mathcal {V}^A\) and \(\mathcal {V}\mapsto \mathcal {V}_B\).
We may consider the relevant question: how much do we learn about semigroups by studying \(\mathcal {L}(\mathcal {C}\mathcal {R})\)? So far, very little, but we learn about the completely regular semigroups. This may best be illustrated on the constructions of, say, completely simple semigroups, normal cryptogroups, cryptogroups, orthogroups, and some other classes including all completely regular semigroups (all this with a unary operation). These constructions point to the unmistakable fact that, even in these few cases, they are quite complex.
Where do we go from here? Formation of \(\mathcal {V}_\theta \) and \(\mathcal {V}^\theta \), where \(\theta \) is a word over a certain alphabet, produces new varieties worthy of consideration. This enlarges the arsenal of “known” varieties and thus enables to climb the lattice \(\mathcal {L}(\mathcal {C}\mathcal {R})\). On the other hand, the upper operators may produce decompositions of \(\mathcal {L}(\mathcal {C}\mathcal {R})\), for example \(\mathcal {V}\mapsto \mathcal {V}^{\mathcal {B}^\wedge }\) associated with the relation \(\mathbf {B}^\wedge \). This is probably the most significant decomposition of \(\mathcal {L}(\mathcal {C}\mathcal {R})\). The operator \(\mathcal {V}\mapsto \mathcal {V}^{\mathcal {B}^\vee }\) shifts all varieties onto the varieties containing all bands, also worthy of detailed scrutiny.
On the other hand, these two mentioned operators represent drop in the bucket for we may, for example, consider \(\mathbf {G}\) and \(\mathbf {CS}\) instead of \(\mathbf {B}\), as studied in [7]. So far, the most fruitful relations have been the kernel and (left, right) trace relations. Hopefully the \(\mathbf {B}^\wedge \)- and \(\mathbf {B}^\vee \)- relations and operators they induce represent a welcome addition.
Rights and permissions
About this article
Cite this article
Petrich, M. Ladders and canonical varieties of completely regular semigroups. Period Math Hung 76, 133–154 (2018). https://doi.org/10.1007/s10998-017-0215-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10998-017-0215-y


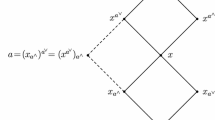
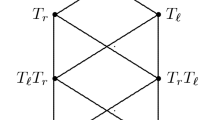
 (d) in D:
(d) in D: 