A DOA Estimation Approach for Transmission Performance Guarantee in D2D Communication

Abstract

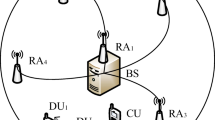
In Device-to-Device (D2D) communications of massive Multiple-Input Multiple-Output (MIMO) system, the inter-channel interference (ICI) can severely deteriorate the entire system performance. The beamforming technique can be used to alleviate this situation. Thus the localization of the users’ equipment (UE) should be known as a prior. In wireless communication, due to the effect of multipath, the model of incident signal should be regarded as distributed sources instead of point sources. In this paper, we propose a 2-D DOA estimation algorithm for coherently distributed (CD) sources based on conformal array. First, three rational invariance relationships are constructed based on generalized steering vectors (GSVs). Then the propagator method (PM) is used for estimating three rational invariance matrices. Finally, the 2-D DOA of CD sources can be obtained from the eigenvalues of three rational invariance matrices. Without spectrum peaking searching, and estimation and eigendecomposition of sampling covariance matrix, the proposed algorithm has low computational complexity. For the condition with a large amount of data, the distributed and parallel PM is proposed to deal with this problem. Simulation results verify the effectiveness of the proposed algorithm.

Appendices

Appendix: The derivation of Eq. 18

Assume that the coordinate of each element is (x _k , y _k , z _k ), k = 1, 2, ⋯, m. The unit vectors of X-axis, Y-axis and Z-axis are given by ${\overrightarrow {\mathbf {e}}_{x}},{\overrightarrow {\mathbf {e}}_{y}}$ and ${\overrightarrow {\mathbf {e}}_{z}}$, respectively. The position vector p _k of kth element is expressed as

$$ {\mathbf{p}_{k}} = {x_{k}}{\overrightarrow {\mathbf{e}}_{x}} + {y_{k}}{\overrightarrow {\mathbf{e}}_{y}} + {z_{k}}{\overrightarrow {\mathbf{e}}_{z}}, $$

(58)

For sub-array 1 and sub-array 2, the elements are arranged on the same generatrix, the X-axis and Y-axis coordinates of the elements in the same generatrix have the relationship x ₁₁ = ⋯ = x _{1(m + 1)} = x ₁ and y ₁₁ = ⋯ = y _{1(m + 1)} = y ₁, respectively. The patterns of the elements in the same generatrix are identical as well, i.e., h ₁₁ = ⋯ = h _{1(m + 1)}. The kth element of the steering vector b ₁(μ _i ) of sub-array 1 can be expressed as

$$\begin{array}{@{}rcl@{}} {\left[ {{\mathbf{b}_{1}}\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}}= \int {\int {{a_{1k}}\left( {\theta ,\varphi } \right)\rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi } } \\ = {H_{1}}\int {\int {\exp \left[ { - jl\left( {k - 1} \right)\cos \theta } \right]\rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi } } , \end{array} $$

(59)

where the kth element of the steering vector of sub-array 1 is a _1k (𝜃,φ) = H ₁ exp[−j l(k−1) cos𝜃] with

$$ {H_{1}} = {h_{1}}\exp\left( { - j2\pi \frac{{{x_{1}}\sin \theta \cos \varphi + {y_{1}}\sin \theta \sin \varphi }}{\lambda }} \right). $$

(60)

The azimuth and elevation DOAs can be expressed as

$$ \theta { = }{\theta_{i}} + \tilde \theta, $$

(61)

$$ \varphi { = }{\varphi_{i}} + \tilde \varphi, $$

(62)

where 𝜃 _i and φ _i are nominal elevation and azimuth of ith CD source, and they are the means of 𝜃 and φ, respectively; $\tilde \theta$ and $\tilde \varphi$ are the corresponding random angular deviations. With the first order Taylor series approximation to a _1k (𝜃,φ) around (𝜃,φ)=(𝜃 _i , φ _i ), we can obtain

$$\begin{array}{@{}rcl@{}} && {a_{1k}}\left( {\theta ,\varphi } \right)= {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\cos \theta } \right]\\ &&={H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\cos \left( {{\theta_{i}} + \tilde \theta } \right)} \right] \\ && = {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\left[ {\cos {\theta_{i}}\cos \tilde \theta - \sin {\theta_{i}}\sin \tilde \theta } \right]} \right] \\ && \approx {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\left( {\cos {\theta_{i}} - \tilde \theta \sin {\theta_{i}}} \right)} \right], \end{array} $$

(63)

where $\cos \tilde \theta \approx 1$ and $\sin \tilde \theta \approx \tilde \theta$ are used in the first inequality for a small angular extension. Then Eq. 59 can be written as

$$\begin{array}{@{}rcl@{}} {\left[ {{\mathbf{b}_{1}}\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}} &=& \int {\int {{a_{1k}}\left( {\theta ,\varphi } \right)\rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi } } \\ & \approx& {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\cos {\theta_{i}}} \right]{\left[ {h\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}}, \end{array} $$

(64)

where

$$\begin{array}{@{}rcl@{}} {\left[ {h\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}} & = &\int \int \exp \left[ {jl\left( {k - 1} \right)\tilde \theta \sin \theta } \right]\\ && \times {\rho_{i}}\left( {{\theta_{i}} + \tilde \theta ,{\varphi_{i}} + \tilde \varphi ;{\boldsymbol{\mu}_{i}}} \right)d\tilde \theta d\tilde \varphi , \end{array} $$

(65)

The kth element of the steering vector b ₂(μ _i ) of sub-array 2 can be expressed as

$$\begin{array}{@{}rcl@{}} {\left[ {{\mathbf{b}_{2}}\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}} &= &\int \int {a_{2k}}\left( {\theta ,\varphi } \right)\exp \left( { - jlcos\theta } \right)\\ &&\times {\rho_{i}}\left( {{\theta_{i}} + \tilde \theta ,{\varphi_{i}} + \tilde \varphi ;{\mu_{i}}} \right)d\tilde \theta d\tilde \varphi \\ &\approx & {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\cos {\theta_{i}}} \right]\\ && \int {\int {\exp \left[ {jl\left( {k - 1} \right)\tilde \theta \sin {\theta_{i}}} \right]} } \\ && \times \exp \left( { - jlcos{\theta_{i}}} \right)\exp \left( {jl\tilde \theta \sin {\theta_{i}}} \right)\\ && \times {\rho_{i}}\left( {{\theta_{i}} + \tilde \theta ,{\varphi_{i}} + \tilde \varphi ;{\boldsymbol{\mu}_{i}}} \right)d\tilde \theta d\tilde \varphi. \end{array} $$

(66)

For a small angular extension and d ₁/λ = 1/4, it follows that $\exp \left ({jl\tilde \theta \sin {\theta _{i}}} \right ) \approx 1$. Then b ₂(μ _i ) can be expressed as

$$\begin{array}{@{}rcl@{}} {\left[ {{\mathbf{b}_{2}}\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}} &\approx & {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\cos {\theta_{i}}} \right]\\ && \times \exp \left( { - jlcos{\theta_{i}}} \right){\left[ {h\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}}. \end{array} $$

(67)

Based on Eqs. 64 and 67, an approximate rotational invariance relationship between b ₁(μ _i ) and b ₂(μ _i ) can be given by

$$ {\mathbf{b}_{2}}\left( {{\boldsymbol{\mu}_{i}}} \right) \approx \exp \left( { - jlcos{\theta_{i}}} \right){\mathbf{b}_{1}}\left( {{\boldsymbol{\mu}_{i}}} \right). $$

(68)

The derivation of Eqs. 24 and 25

For sub-array 3, the X-axis and Y-axis coordinates of the elements in the same generatrix have the relationship x _{3(m + 3)} = x _{3(m + 4)}⋯ = x _{3(2m + 2)} = x ₃ and y _{3(m + 3)} = y _{3(m + 4)}⋯ = y _{3(2m + 2)} = y ₃, respectively. The patterns of the elements in the same generatrix are identical as well, i.e., h _{3(m + 3)} = h _{3(m + 4)}⋯ = h _{3(2m + 2)}. The kth element of the steering vector b ₃(μ _i ) of sub-array 3 can be expressed as

$$\begin{array}{@{}rcl@{}} {\left[ {{b_{3}}\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}}\! &=& \int {\int {{a_{3k}}\left( {\theta ,\varphi } \right)\rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi } } \\ & =&{H_{3}}\int \int \exp \left[ { - jl\left( {k - 1} \right)\cos \theta } \right] \\ & &\times \exp \left( { - j{\omega_{2}}} \right)\rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi \\ & =&{H_{3}}\int {\int {\exp \left[ { - jl\left( {k - 1} \right)\cos \theta } \right]} } \\ & &\times \exp \left[ { \!\!- jl\!\left( {\frac{1}{2}\sin \theta \cos \varphi \!+ \frac{{\sqrt 3 }}{2}\sin \theta \sin \varphi } \!\right)} \right]\\ & &\times \rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi, \end{array} $$

(69)

where $\exp \left (- j\omega _{2i} \right ) = \exp [ - jl(\frac {1}{2}\sin \theta \cos \varphi + \frac {\sqrt {3}}{2}\sin \theta \sin \varphi )]$ according to Eqs. 8 and 11; the kth element of the steering vector of sub-array 1 is a _3k (𝜃,φ) = H ₃ exp[−j l(k−1) cos𝜃] with

$$ {H_{3}} = {h_{3}}\exp\left( { - j2\pi \frac{{{x_{3}}\sin \theta \cos \varphi + {y_{3}}\sin \theta \sin \varphi }}{\lambda }} \right). $$

(70)

With the first order Taylor series approximation to $\exp \left ({ - \frac {1}{2}jl\sin \theta \cos \varphi } \right )$ and $\exp \left ({ - \frac {{\sqrt 3 }}{2}jl\sin \theta \sin \varphi } \right )$, we respectively have

$$\begin{array}{@{}rcl@{}} &&\exp \left( { - \frac{1}{2}jl\sin \theta \cos \varphi } \right) \\ && = \exp \left[ { - \frac{1}{2}jl\sin \left( {{\theta_{i}} + \tilde \theta } \right)\cos \left( {{\varphi_{i}} + \tilde \varphi } \right)} \right] \\ && \approx \exp \left[ { - \frac{1}{2}jl\left( {\sin {\theta_{i}} + \tilde \theta \cos {\theta_{i}}} \right)\left( {\cos {\varphi_{i}} + \tilde \varphi \sin {\varphi_{i}}} \right)} \right] \\ && \approx \exp \left( { - \frac{1}{2}jl\sin {\theta_{i}}\cos {\varphi_{i}}} \right) \\ && \quad\times \exp \left[ { - \frac{1}{2}jl\left( {\tilde \theta \cos {\theta_{i}}\cos {\varphi_{i}} - \tilde \varphi \sin {\varphi_{i}}\sin {\theta_{i}}} \right)} \right] \end{array} $$

(71)

and

$$\begin{array}{@{}rcl@{}} && \exp \left( { - \frac{{\sqrt 3 }}{2}jl\sin \theta \sin \varphi } \right) \\ && = \exp \left[ { - \frac{{\sqrt 3 }}{2}jl\sin \left( {{\theta_{i}} + \tilde \theta } \right)\sin \left( {{\varphi_{i}} + \tilde \varphi } \right)} \right] \\ && \approx \exp \left[ { - \frac{{\sqrt 3 }}{2}jl\left( {\sin {\theta_{i}} + \tilde \theta \cos {\theta_{i}}} \right)\left( {\sin {\varphi_{i}} + \tilde \varphi \cos {\varphi_{i}}} \right)} \right] \\ && \approx \exp \left( { - \frac{{\sqrt 3 }}{2}jl\sin {\theta_{i}}\sin {\varphi_{i}}} \right) \\ &&\quad \times \exp \left[ { - \frac{{\sqrt 3 }}{2}jl\left( {\tilde \theta \cos {\theta_{i}}\sin {\varphi_{i}} + \tilde \varphi \cos {\varphi_{i}}\sin {\theta_{i}}} \right)} \right] \end{array} $$

(72)

For a small angular extension and d ₂/λ = 1/4, it follows that $\exp \left [ { - \frac {1}{2}jl\left ({\tilde \theta \cos {\theta _{i}}\cos {\varphi _{i}} - \tilde \varphi \sin {\varphi _{i}}\sin {\theta _{i}}} \right )} \right ] \approx 1$ and $\exp \left [ { - \frac {{\sqrt 3 }}{2}jl\left ({\tilde \theta \cos {\theta _{i}}\sin {\varphi _{i}} + \tilde \varphi \cos {\varphi _{i}}\sin {\theta _{i}}} \right )} \right ] \approx 1$. The kth element of the steering vector b ₃(μ _i ) of sub-array 3 can be expressed as

$$\begin{array}{@{}rcl@{}} && {\left[ {{\mathbf{b}_{3}}\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}} = \int \int {a_{3k}}\left( {\theta ,\varphi } \right) \rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi \\ && \approx {H_{1}}\exp \left[ { - jl\left( {k - 1} \right)\cos {\theta_{i}}} \right]\\ &&\quad \times \exp \left[ { - jl\left( {\frac{1}{2}\sin {\theta_{i}}\cos {\varphi_{i}} - \frac{{\sqrt 3 }}{2}\sin {\theta_{i}}\sin {\varphi_{i}}} \right)} \right] \\ && \quad\times \int {\int {\exp \left[ {jl\left( {k - 1} \right)\tilde \theta \sin {\theta_{i}}} \right]\rho \left( {\theta ,\varphi ;{\boldsymbol{\mu}_{i}}} \right)d\theta d\varphi } } \\ && \approx {H_{3}}\exp \left[ { - jl\left( {k - 1} \right)\cos {\theta_{i}}} \right]\exp \left( { - j{\omega_{2i}}} \right){\left[ {h\left( {{\boldsymbol{\mu}_{i}}} \right)} \right]_{k}}. \end{array} $$

(73)

Based on Eqs. 59 and 73, an approximate rotational invariance relationship between b ₁(μ _i ) and b ₃(μ _i ) can be given by

$$ {\mathbf{b}_{3}}\left( {{\boldsymbol{\mu}_{i}}} \right) \approx \frac{{{H_{3}}}}{{{H_{1}}}}\exp \left( { - j{\omega_{2i}}} \right){\mathbf{b}_{1}}\left( {{\boldsymbol{\mu}_{i}}} \right). $$

(74)

Similar as Eq. 74, an approximate rotational invariance relationship between b ₁(μ _i ) and b ₄(μ _i ) can be given by

$$ {\mathbf{b}_{4}}\left( {{\boldsymbol{\mu}_{i}}} \right) \approx \frac{{{H_{4}}}}{{{H_{1}}}}\exp \left( { - j{\omega_{3i}}} \right){\mathbf{b}_{1}}\left( {{\boldsymbol{\mu}_{i}}} \right), $$

(75)

where the form of H ₄ is similar with that of H ₃.