Abstract
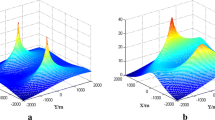
Angularly dependent gain and phase uncertainties are produced by the combined effects of multiple sensor errors. This paper proposes a direction-finding method for noncircular signals in the presence of angularly dependent gain/phase errors, which utilizes instrumental sensors to achieve auto-calibration and relies on an improved alternating projection procedure. By applying the principle of the extended 2-sided instrumental variable signal subspace fitting algorithm, the proposed method is effective for separating spatially and temporally correlated noncircular sources from the unknown colored (i.e., spatially correlated) noise. Considering that modeling errors of instrumental sensors are frequently encountered in practice, this paper also presents a theoretical derivation for the closed-form expression of the mean square error of the estimation under the influence of modeling errors of instrumental sensors in the first-order analysis. Finally, the results of two series of simulations are demonstrated. The first series of simulations verifies the effectiveness of the proposed auto-calibration method, and shows that noncircularity and temporal correlation of sources are informative for enhancing the calibration performance of our method. The results also prove that the proposed method performs better than the instrumental sensor method when applied to spatially and temporally correlated noncircular sources. Moreover, this performance advantage of our method is more prominent when signal-to-noise ratio is low, or in spatially correlated noise fields. The second series of simulations validates the theoretical prediction, and thus our statistical analysis has a high predictive value for calibration performance of the proposed method under the influence of modeling errors.
















Similar content being viewed by others
References
Abeida, H., & Delmas, J.-P. (2006). MUSIC-like estimation of direction of arrival for noncircular sources. IEEE Transactions on Signal Processing, 54(7), 2678–2690.
Chargé, P., Wang, Y. D., & Saillard, J. (2000). A direction finding method under sensor gain/phase uncertainties. In Proceedings of the IEEE international conference on acoustics, speech and signal processing (Vol. 5, pp. 3045–3048). Istanbul, Turkey: IEEE Press.
Chargé, P., Wang, Y., & Saillard, J. (2001). A noncircular sources direction finding method using polynomial rooting. Signal Processing, 81(6), 1765–1770.
Ferréol, A., Larzabal, P., & Viberg, M. (2008). Performance prediction of maximum-likelihood direction-of-arrival estimation in the presence of modeling errors. IEEE Transactions on Signal Processing, 56(10), 4785–4793.
Ferréol, A., Larzabal, P., & Viberg, M. (2010). Statistical analysis of the MUSIC algorithm in the presence of modeling errors, taking into account the resolution probability. IEEE Transactions on Signal Processing, 58(8), 4156–4166.
Goossens, R., & Rogier, H. (2007). A hybrid UCA-RARE/Root-MUSIC approach for 2-D direction of arrival estimation in uniform circular arrays in the presence of mutual coupling. IEEE Transactions on Antennas and Propagation, 55(3), 841–849.
Haddadi, F., & Nayebi, M. M. (2009). Direction-of-arrival estimation for temporally correlated narrowband signals. IEEE Transactions on Signal Processing, 57(2), 600–609.
Hassen, S. B., Bellili, F., & Samet, A. (2011). DOA estimation of temporally and spatially correlated narrowband noncircular sources in spatially correlated white noise. IEEE Transactions on Signal Processing, 59(9), 4108–4121.
Moses, R. L., & Beex, A. A. (1988). Instrumental variable adaptive array processing. IEEE Transactions on Aerospace and Electronic Systems, 24(2), 192–202.
Pesavento, M., & Gershman, A. B. (2001). Maximum-likelihood direction-of-arrival estimation in the presence of unknown nonuniform Noise. IEEE Transactions on Signal Processing, 49(7), 1310–1324.
Pesavento, M., Gershman, A. B., & Wong, K. M. (2002). Direction finding in partly-calibrated sensor arrays composed of multiple subarrays. IEEE Transactions on Signal Processing, 50, 2103–2115.
Picinbono, B. (1994). On circularity. IEEE Transactions on Signal Processing, 24(12), 3473–3482.
Soderstrom, T., & Stoica, P. (1983). Instrumental variable methods for system identification. Berlin: Springer.
Stoica, P., Viberg, M., & Ottersten, B. (1994). Instrumental variable approach to array processing in spatially correlated noise fields. IEEE Transactions on Signal Processing, 42(1), 121–133.
Viberg, M., Ottersten, B., & Kailath, T. (1991). Detection and estimation in sensor arrays using weighted subspace fitting. IEEE Transactions on Signal Processing, 39(11), 2436–2449.
Viberg, M., Stoica, P., & Ottersten, B. (1995). Array processing in correlated noise fields based on instrumental variables and subspace fitting. IEEE Transactions on Signal Processing, 43(5), 1187–1199.
Wang, B., Wang, Y., & Chen, H. (2003). Array calibration of angularly dependent gain/phase uncertainties with instrumental sensors. IEEE international symposium on phased array systems and technology (pp. 182–186).
Wang, D., Pan, M., & Ying, W. (2011). Maximum likelihood self-calibration for direction-dependent gain-phase errors with carry-on instrumental sensors:case of deterministic signal model. Journal on Communications, 32(2), 34–47.
Wax, M., & Ziskind, I. (1989). On unique localization of multiple sources by passive sensor arrays. IEEE Transactions on Acoustics, Speech and Signal Processing, 37(7), 996–1000.
Xianda, Z. (2004). Matrix analysis and application. Beijing: Tsinghua University Press.
Yang, L., & Ho, K. C. (2010). Alleviating sensor position error in source location using calibration emitters at inaccurate locations. IEEE Transactions on Signal Processing, 58(1), 67–83.
Ziskind, I., & Wax, M. (1988). Maximum likelihood localization of multiple sources by alternating projection. IEEE Transactions on Acoustics, Speech and Signal Processing, 36(11), 1553–1560.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by the National Natural Science Foundation of China under Grant 61201381 and the Future Development Foundation of Zhengzhou Information Science and Technology College under Grant YP12JJ202057.
Appendices
Appendix 1
Proof of (51):
First, introduce Lemma 1.
Lemma 1
(Xianda 2004) If \(\varvec{A}\) is a matrix function of \({\varvec{\gamma }}\in {\mathbb {R}}^{K\times 1}\), then the first-order partial derivative of \({\varvec{\varPi } }_{\varvec{A}}^\bot \) with respect to \({\varvec{\gamma } }_i \left( {i=1,2\ldots K} \right) \) is
Starting from Lemma 1, we obtain the following expression of the first-order partial derivative of \(V\left( {{\varvec{\varTheta } },{\varvec{\varepsilon } }} \right) \) with respect to parameter \(\alpha \in {\varvec{\varTheta } }\):
where \(\varvec{\tilde{B}}^{(\alpha )}\left( {\varvec{\varTheta } } \right) =\frac{\partial \varvec{\tilde{B}}\left( {\varvec{\varTheta } } \right) }{\partial \alpha }\).
By applying the first-order perturbation analysis approach, we ignore the infinitesimal \(o\left( {\left\| {\varvec{\varepsilon }} \right\| _2 } \right) \). Thus using the approximation \(\varvec{\hat{{\tilde{\varSigma }}}}^{\mathrm{H}}\varvec{\tilde{R}}_{\varvec{\psi } }^{-1} \varvec{\hat{{\tilde{\varSigma }}}}\approx \varvec{\hat{{V}}}_s {\varvec{\varLambda } }_s^{2}\varvec{\hat{{V}}}_s^{\mathrm{H}}\), \(V_{{{\varvec{\varepsilon } }}}^{(\alpha )} \left( {{\varvec{\bar{{\varTheta }}}}} \right) \) can be approximated as
where \(\varvec{\tilde{B}}\) and \(\varvec{\tilde{B}}^{(\alpha )}\) are short for \(\varvec{\tilde{B}}\left( {{\varvec{\bar{{\varTheta }}}}} \right) \) and \(\varvec{\tilde{B}}^{(\alpha )}\left( {{\varvec{\bar{{\varTheta }}}}} \right) \), respectively. Then substituting
and (44), (45) into (62), some algebraic manipulations yield
Next we proceed to reduce \(\varvec{\hat{{B}}}\varvec{\mathcal {Q}} \varvec{\mathcal {\hat{{\tilde{B}}}}}_D^\mathrm{H} \varvec{\tilde{R}}_{\varvec{\psi } }^{-1} \varvec{\mathcal {\hat{{\tilde{B}}}}}_D \varvec{\mathcal {Q}}^{\mathrm{H}} \varvec{\hat{{B}}}^{\mathrm{H}}\) in (64).
We have
which follows from \(\varvec{\hat{{B}}}=\varvec{B}+\varvec{E}\). Ignore the infinitesimal \(o\left( {\left\| {\varvec{\varepsilon } } \right\| _2} \right) \) in (65) and then insert it into (64). With the use of \(\varvec{B}^{\mathrm{H}}\varvec{c}^{-1/2}{\varvec{\varPi } }_{\varvec{c}^{-1/2}\varvec{B}}^\bot = \varvec{O}\) and \(\left( {\varvec{c}^{-1/2}\varvec{B}} \right) ^{\dagger }\varvec{c}^{-1/2}\varvec{B}=\varvec{I}_N\), we can approximate (64) as
Moreover, for \(\alpha \in {\varvec{\eta } }_n \left( {n=1,2\ldots N} \right) \), we have
where \(\varvec{b}_n^{(\alpha )}=\left. {\frac{\partial \varvec{b}\left( {\varvec{\eta } } \right) }{\partial \alpha }} \right| \;_{{\varvec{\eta } }=\varvec{\bar{{\eta }}}_n }\) and \(\varvec{e}_n^N \in {\mathbb {R}}^{N\times 1}\) is the unit vector with the \(n\)th element being one. By applying the readily-checked formula (Xianda 2004)
which holds for arbitrary matrices \(\varvec{E}, \varvec{F}\) and \(\varvec{G}\), we have the following expression after substituting (67) into (66):
Because \(\varvec{\mathcal {Q}}\varvec{\mathcal {\tilde{B}}}_D^\mathrm{H} \varvec{\tilde{R}}_{\varvec{\psi } }^{-1} \varvec{\mathcal {B}}_D \varvec{\mathcal {Q}}^{\mathrm{H}}\varvec{e}_n^N\) is the \(n\)th column of the matrix \(\varvec{U}=\varvec{\mathcal {Q}}\varvec{\mathcal {\tilde{B}}}_D^\mathrm{H} \varvec{\tilde{R}}_{\varvec{\psi } }^{-1} \varvec{\mathcal {\tilde{B}}}_D \varvec{\mathcal {Q}}^{\mathrm{H}}\) and \(\varvec{b}_n^{(\alpha )\hbox {H}} \varvec{c}^{-1/2}{\varvec{\varPi }}_{\varvec{c}^{-1/2}\varvec{B}}^\bot \varvec{c}^{-1/2}\) is one line of the matrix \(\varvec{D}^{\mathrm{H}} \varvec{c}^{-1/2}{\varvec{\varPi }}_{\varvec{c}^{-1/2}\varvec{B}}^\bot \varvec{c}^{-1/2}\), we conclude from (69):
which is the expression of \(\varvec{V}_{\varvec{\varepsilon } }^{({\varvec{\varTheta } })} \left( {{\varvec{\bar{{\varTheta }}}}} \right) \) given in (51).
Appendix 2
Proof of (52):
To begin with, we will first introduce Lemma 2.
Lemma 2
(Xianda 2004) If \(\varvec{A}\) is a matrix function of \({\varvec{\gamma } }\in {\mathbb {R}}^{K\times 1}\), then the second-order partial derivative of \({\varvec{\varPi } }_{\varvec{A}}^\bot \) with respect to \({\varvec{\gamma } }_i \left( {i=1,2\ldots K} \right) \) and \({\varvec{\gamma } }_j \left( {j=1,2\ldots K} \right) \) is
Here, \(( \cdots )^{\mathrm{H}}\) represents the conjugate transpose of all the terms on the right-side of the equation.
Discarding terms which result in contributions of the order \(o\left( {\left\| {\varvec{\varepsilon } } \right\| _2} \right) , \varvec{H}_{\varvec{\varepsilon } } \left( {{\varvec{\bar{{\varTheta }}}}} \right) \) can be approximated as (Ferréol et al. 2008)
To derive the expression of \({\mathop {{\lim }}\limits _{{\varvec{\varepsilon } }\rightarrow \varvec{0}}} \varvec{H}_{\varvec{\varepsilon } } \left( {{\varvec{\bar{{\varTheta }}}}} \right) \), we compute the second-order partial derivative of \(V\left( {{\varvec{\varTheta } },{\varvec{\varepsilon } }} \right) \) with respect to \(\alpha \in {\varvec{\eta } }_n,\beta \in {\varvec{\eta } }_m \left( {n,m=1,2\ldots N} \right) \) according to Lemma 2:
Here, we have \({\varvec{\varLambda } }_s\) for \(\varvec{\hat{{\varLambda }}}_s\) when \({\varvec{\varepsilon } }\rightarrow \varvec{0}\). And \(\left( {\varvec{c}^{-1/2}\varvec{B}} \right) ^{\dagger }\varvec{c}^{-1/2}\varvec{B}=\varvec{I}_N, \varvec{B}^{\mathrm{H}}\varvec{c}^{-1/2}{\varvec{\varPi } }_{\varvec{c}^{-1/2}\varvec{B}}^\bot =\varvec{O}\), \(\varvec{\tilde{\varSigma }}^{\mathrm{H}}\varvec{\tilde{R}}_{\varvec{\psi } }^{-1} \varvec{\tilde{\varSigma }}=\varvec{V}_s {\varvec{\varLambda } }_s^{2}\varvec{V}_s^{\mathrm{H}}\) are used in (73).
Let \(i_\alpha \) and \(i_\beta \) indicate the column numbers of \(\varvec{b}_n^{(\alpha )}\) and \(\varvec{b}_n^{(\beta )}\) in \(\varvec{D}\), respectively. Then following from (67), the formula above can be rewritten by
Combining (73) and (74), it can be concluded by applying \(\varvec{U}=\varvec{\mathcal {Q}\mathcal {\tilde{B}}}_D^\mathrm{H} \varvec{\tilde{R}}_{\varvec{\psi }}^{-1} \varvec{\mathcal {\tilde{B}}}_D \varvec{\mathcal {Q}}^{\mathrm{H}}\):
Up to this point, the expression in (52) is proved.
Appendix 3
Proof of (55):
Deriving from (50), we have
where \(\varvec{H}_0 \!=\!\frac{1}{4}\varvec{H}_{\varvec{\varepsilon } } \left( {{\varvec{\bar{{\varTheta }}}}} \right) =\hbox {Re}\left\{ {\left( {\left( {\varvec{1}_{\left( {2K+1} \right) } \varvec{1}_{(2K+1)}^\mathrm{T} } \right) \otimes \varvec{U}} \right) ^{\mathrm{T}}\circ \left( {\varvec{D}^{\mathrm{H}}\varvec{c}^{-1/2}{\varvec{\varPi } }_{\varvec{c}^{-1/2}\varvec{B}}^\bot \varvec{c}^{-1/2}\varvec{D}} \right) } \right\} \).
By using \(\varvec{G}=\left( {\varvec{1}_{\left( {2K+1} \right) } \otimes \varvec{U}} \right) ^{\mathrm{T}}{*}\left( {\varvec{c}^{-1/2}{\varvec{\varPi } }_{\varvec{c}^{-1/2}\varvec{B}}^\bot \varvec{c}^{-1/2}\varvec{D}} \right) \), we have \(\varvec{V}_{\varvec{\varepsilon } }^{({\varvec{\varTheta } })} \left( {{\varvec{\bar{{\varTheta }}}}} \right) \approx -4\hbox {Re}\left\{ {\varvec{G}^{\mathrm{H}}\varvec{J\varepsilon }} \right\} \). Moreover, we obtain the following expression with the help of the equality of \(\hbox {Re}\left\{ \varvec{u} \right\} \hbox {Re}\left\{ {\varvec{u}^{\mathrm{T}}} \right\} =\frac{1}{2}\hbox {Re}\left\{ {\varvec{uu}^{\mathrm{T}}+\varvec{uu}^{\mathrm{H}}} \right\} \):
After applying \(\hbox {E}\left[ {{\varvec{\varepsilon \varepsilon }}^{\mathrm{T}}} \right] =\varvec{O}\) due to the circularly symmetric assumption of the modeling errors, the expectation of the random matrix above is obtained:
Upon the substitution of (78) into (76), the proof of (55) is completed.
Rights and permissions
About this article
Cite this article
Yin, Jx., Wu, Y. & Wang, D. An auto-calibration method for spatially and temporally correlated noncircular sources in unknown noise fields. Multidim Syst Sign Process 27, 511–539 (2016). https://doi.org/10.1007/s11045-015-0316-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11045-015-0316-9