Skip to main content
SpringerLink
Log in

A transformed jump-adapted backward Euler method for jump-extended CIR and CEV models

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

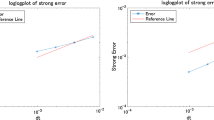
A novel time-stepping scheme, called transformed jump-adapted backward Euler method, is developed in this paper to simulate a class of jump-extended CIR and CEV models. The proposed scheme is able to preserve the positivity of the underlying problems. Furthermore, its strong convergence rate of order one is recovered for the considered models with non-Lipschitz diffusion coefficients. Numerical examples are finally reported to confirm our theoretical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahn, C.M., Thompson, H.E.: Jump-diffusion processes and the term structure of interest rates. J. Financ. 43(1), 155–174 (1988)

    Article  MathSciNet  Google Scholar 

  2. Alfonsi, A.: On the discretization schemes for the CIR (and Bessel squared) processes. Monte Carlo Methods Appl. 11(4), 355–384 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  3. Alfonsi, A.: High order discretization schemes for the CIR process: application to affine term structure and Heston models. Math. Comput. 79(269), 209–237 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Alfonsi, A.: Strong order one convergence of a drift implicit Euler scheme: application to the CIR process. Stat. Probab. Lett. 83(2), 602–607 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Beliaeva, N., Nawalkha, S.: Pricing American interest rate options under the jump-extended constant-elasticity-of-variance short rate models. J. Bank. Financ. 36 (1), 151–163 (2012)

    Article  Google Scholar 

  6. Bossy, M., Diop, A.: An efficient discretisation scheme for one dimensional SDEs with a diffusion coefficient function of the form |x|a,a[1/2, 1) Preprint (2007)

  7. Berkaoui, A., Bossy, M., Diop, A.: Euler scheme for SDEs with non-Lipschitz diffusion coefficient: strong convergence. ESAIM Probab. Stat. 12, 1–11 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bruti-Liberati, N., Platen, E.: Strong approximations of stochastic differential equations with jumps. J. Comput. Appl. Math. 205, 982–1001 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chalmers, G.D., Higham, D.J.: First and second moment reversion for a discretized square root process with jumps. J. Differ. Equ. Appl. 16, 143–156 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cont, R., Tankov, P.: Financial Modelling with Jump Processes, Financial Mathematics Series, Chapman & hall/CRC, London Boca Raton (2004)

  11. Dereich, S., Neuenkirch, A., Szpruch, L.: An Euler-type method for the strong approximation of the Cox-Ingersoll-Ross process. Proc. R. Soc. A Math. Phys. Eng. Sci. 468(2140), 1105–1115 (2012)

    Article  MathSciNet  Google Scholar 

  12. Gardoń, A.: The order of approximations for solutions of Itô-Type stochastic differential equations with jumps. Stoch. Anal. Appl. 22(3), 679–699 (2004)

    Article  MATH  Google Scholar 

  13. Gyöngy, I., Rásonyi, M.: A note on Euler approximations for SDEs with Hölder continuous diffusion coefficients. Stoch. Process. Appl. 121(10), 2189–2200 (2011)

    Article  MATH  Google Scholar 

  14. Halidias, N.: An explicit and positivity preserving numerical scheme for the mean reverting CEV model, arXiv preprint arXiv:1501.03434 (2015)

  15. Halley, W., Malham, S.J.A., Wiese, A.: Positive and implicit stochastic volatility simulation, Arxiv preprint arXiv:0802.4411. 2008 arxiv.org.

  16. Higham, D.J., Kloeden, P.E.: Numerical methods for nonlinear stochastic differential equations with jumps. Numer. Math. 101(1), 101–119 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  17. Higham, D.J., Mao, X.: Convergence of Monte Carlo simulations involving the mean-reverting square root process. J. Comput. Financ. 8, 35–61 (2005)

    Article  Google Scholar 

  18. Higham, D.J., Mao, X., Szpruch, L.: Convergence, non-negativity and stability of a new Milstein scheme with applications to finance. Discret. Contin. Dyn. Syst. Ser. B 18(8), 2083–2100 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Hutzenthaler, M., Jentzen, A., Noll, M.: Strong convergence rates and temporal regularity for Cox-Ingersoll-Ross processes and Bessel processes with accessible boundaries arXiv:1403.6385v1 (2014)

  20. Kahl, C., Günthera, M., Rossberg, T.: Structure preserving stochastic integration schemes in interest rate derivative modeling. Appl. Numer. Math. 58(3), 284–295 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. Karatzas, I., Shreve, S.E.: Brownian Motion and Stochastic Calculus Springer Science & Business Media (1991)

  22. Moro, E., Schurz, H.: Boundary preserving semianalytical numerical algorithms for stochastic differential equations. SIAM J. Sci. Comput. 29(4), 1525–1549 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  23. Neuenkirch, A., Szpruch, L.: First order strong approximations of scalar SDEs defined in a domian. Numer. Math. 128(1), 103–136 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  24. Platen, E.: An approximation method for a class of Itô processes with jump component. Liet. Mat. Rink 22(2), 124–136 (1982)

    MathSciNet  MATH  Google Scholar 

  25. Platen, E., Bruti-Liberati, N.: Numerical solution of stochastic differential equations with jumps in finance Springer Science & Business Media (2010)

  26. Sun, X., Gan, S.: An efficient semi-analytical simulation for the heston model. Comput. Econ. 43(4), 433–445 (2014)

    Article  Google Scholar 

  27. Wu, F., Mao, X., Chen, K.: Strong convergence of Monte Carlo simulations of the mean-reverting square root process with jump. Appl. Math. Comput. 206(2), 494–505 (2008)

    MathSciNet  MATH  Google Scholar 

  28. Wu, Y.: Jump-diffusion CIR model and its applications in credit risk. Hacet. J. Math. Stat. 43(6), 1095–1106 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, Shandong, China

    Xu Yang

  2. School of Mathematics and Statistics, Central South University, Changsha, 410083, Hunan, China

    Xiaojie Wang

Authors
  1. Xu Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaojie Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaojie Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, X., Wang, X. A transformed jump-adapted backward Euler method for jump-extended CIR and CEV models. Numer Algor 74, 39–57 (2017). https://doi.org/10.1007/s11075-016-0137-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-016-0137-4

Keywords

Mathematics Subject Classification (2010)

Search

Navigation