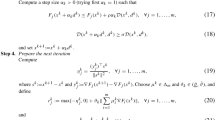Stepsize domain confirmation and optimum of ZeaD formula for future optimization

Abstract

Future optimization, which is also known as discrete-time time-variant optimization problem, is an important issue in scientific fields. Recently, Guo et al. have proposed a new effective three-step discrete-time zeroing dynamics (DTZD) model (Guo et al. Numer. Algorithms 77(1), 23–36, 2018) to solve future optimization problems, which is discretized from continuous-time zeroing dynamics (CTZD) model via utilizing a type of Zhang et al. discretization (ZeaD) formula whose coefficients are proportional to $6,~3,~2$, and 1 (termed as ZeaD formula 6321). In this paper, we mainly focus on the stability of this DTZD model. There is an important parameter that closely relates to the stability of the DTZD model, which is called stepsize. Through theoretical study, we obtain the accurate stepsize domain, which makes the DTZD model stable, and the result, i.e., stepsize $h\in (0,0.8)$, confirms Guo et al.’s previous investigation. Furthermore, the optimum of the stepsize, which makes the DTZD model converge fastest to steady state in terms of residual error and also provides the best stability (i.e., most away from unstable state), is discussed and investigated as well on the basis of theoretical derivation. Eventually, numerical experiments are carried out to confirm again the correctness of the stepsize domain and the optimum in the DTZD model for future optimization.

Appendices

Appendix A

We have the following four results for an N-step method [19, 20].

Result 1: :

An N-step method $\sum \nolimits _{i = 0}^{N} {\alpha _{i} z_{k+i}}=\tau \sum \nolimits _{i = 0}^{N} \beta _{i}\vartheta _{k+i}$ can be checked for 0-stability by determining the roots of its characteristic polynomial $P_{N}(\lambda ) = \sum \nolimits _{i = 0}^{N} \alpha _{i}\lambda ^{i}$. If all roots denoted by $\lambda$ of the polynomial $P_{N}(\lambda )$ satisfy $|\lambda |\leq 1$ with $|\lambda |= 1$ being simple, then the corresponding N-step method is 0-stable (i.e., has 0-stability).

Result 2: :

An N-step method is said to be consistent of order k if the truncation error for the exact solution is of order $O(\tau ^{k + 1})$ where $k>0$.

Result 3: :

An N-step method is convergent, i.e., $z_{[(t-t_{0})/\tau ]} \rightarrow z^{*}(t)$, for all $t\in [t_{0},t_{\text {f}}]$, as $\tau \rightarrow 0$, if and only if the method is 0-stable and consistent.

Result 4: :

A 0-stable consistent method converges with the order of its truncation error.

Appendix B

• 1. Via Fan equations [21], an univariate cubic equation with $a,b,c,d\in \mathbb {R}$ and $a\ne 0$, i.e.,

  $$ax^3+bx^2+cx+d = 0,$$

  can be solved by using the following steps.

  The discriminant of the cubic equation is define as

  $${\Delta}=B^2-4AC, $$

  where

  $$\left\{\begin{array}{cc} &A=b^2-3ac,\\ &B=bc-9ad,\\ &C=c^2-3bd. \end{array}\right. $$

  • (1). When $A=B = 0,$ the roots of the equation can be formulated as

    $$\lambda_1=\lambda_2=\lambda_3=-\frac{b}{3a}=-\frac{c}{b}=-\frac{3d}{c}. $$

  • (2). When ${\Delta }>0,$ the roots of the cubic equation can be formulated as

    $$\begin{array}{@{}rcl@{}} &&\lambda_{1}=\frac{1}{3a}\left( {-b-\left( \sqrt[3]{{y_{1}}}+\sqrt[3]{y_{2}}\right)}\right),\\ &&\lambda_{2}=\frac{1}{6a}\left( {-2b+(\sqrt[3]{y_{1}}+\sqrt[3]{y_{2}})+\sqrt{3}\left( \sqrt[3]{y_{1}}-\sqrt[3]{y_{2}}\right)\mathrm{i}}\right),\\ &&\lambda_{3}=\frac{1}{6a}\left( {-2b+(\sqrt[3]{y_{1}}+\sqrt[3]{y_{2}})-\sqrt{3}\left( \sqrt[3]{y_{1}}-\sqrt[3]{y_{2}}\right)\mathrm{i}}\right), \end{array} $$

    with

    $$y_{1}=Ab+ 3a\left( \frac{-B+\sqrt{{\Delta}}}{2}\right),~y_{2}=Ab+ 3a\left( \frac{-B-\sqrt{{\Delta}}}{2}\right), $$

    and with i denoting the imaginary unit.

  • (3). When ${\Delta }= 0,$ the roots of the cubic equation can be formulated as

    $$\lambda_1=-\frac{b}{a}+\frac{B}{A},~\lambda_2=\lambda_3=-\frac{B}{2A}, $$

    where $A\ne 0$.

  • (4). When ${\Delta }<0,$ the roots of the cubic equation can be formulated as

    $$\begin{array}{@{}rcl@{}} &&\lambda_1=-\frac{1}{3a}\left( b-\sqrt{A}\left( \cos\left( {\frac{\theta}{3}}\right)+\sqrt{3}\sin\left( {\frac{\theta}{3}}\right)\right)\right),\\ &&\lambda_2=-\frac{1}{3a}\left( b + 2\sqrt{A}\cos\left( {\frac{\theta}{3}}\right)\right),\\ &&\lambda_3=-\frac{1}{3a}\left( b-\sqrt{A}\left( \cos\left( {\frac{\theta}{3}}\right)-\sqrt{3}\sin\left( {\frac{\theta}{3}}\right)\right)\right), \end{array} $$

    where

    $$\theta=\arccos\left( \frac{2Ab-3aB}{2A^{\frac{3}{2}}}\right). $$

• 2. According to Fan’s distinguishing means, the number and types of roots is determined by the discriminant of the cubic equation.

  • (1). If $A=B = 0,$ the equation has a real triple root.

  • (2). If ${\Delta }>0,$ the equation has a real root and two complex conjugate roots.

  • (3). If ${\Delta }= 0,$ the equation has a multiple root and all of its roots are real.

  • (4). If ${\Delta }<0,$ the equation has three distinct real roots.

Appendix C

Vieta’s formula [23] is represented as follows. Any general polynomial with $a_{n}\ne 0$ of degree n, i.e.,

$$P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+a_{1}x+a_{0},$$

has n (not necessarily distinct) complex roots $\lambda _{1}, \lambda _{2},\cdots , \lambda _{n}$. The relationship between the roots and the coefficients of the polynomial is as follows:

$$\sum\limits_{1\le i_{1}<i_{2}<\cdots<i_{k}\le n}\lambda_{i_{1}}\lambda_{i_{2}}{\cdots} \lambda_{i_{k}}=(-1)^{k}\frac{a_{n-k}}{a_{n}}, $$

where $k = 1,2,\cdots ,n$, and $i_k$ is in increasing order to ensure that each subproduct of roots is used exactly once.