Wigner–Yanase skew information and quantum phase transition in one-dimensional quantum spin-1/2 chains

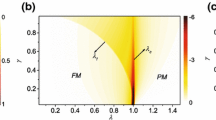
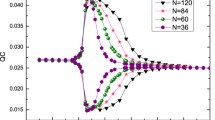
Abstract

The quantum coherence based on Wigner–Yanase skew information and its relations with quantum phase transitions (QPTs) in one-dimensional quantum spin-1/2 chains are studied. Different from those at the critical point (CP) of the Ising transition in the transverse-field XY chain, the single-spin quantum coherence and the two-spin local $\sigma ^z$ quantum coherence are extremal at the CP of the anisotropy transition, and the first-order derivatives of the two-spin local $\sigma ^x$ and $\sigma ^y$ quantum coherence have logarithmic divergence with the chain size. For the QPT between the gapped and gapless phases in the chain with three-spin interactions, however, no finite-size scaling behavior of the derivatives of quantum coherence is found.

Appendix: The root of the two-spin density matrix \(\rho _{AB}\)

The density matrix of a two-spin reduced state in the representation spanned by the natural basis has the general form

$$\begin{aligned} \rho _{AB}=\left( {\begin{array}{*{20}c} {\rho _{11}} &{} 0 &{} 0 &{} {\rho _{14}}\\ 0 &{} {\rho _{22}} &{} {\rho _{23}} &{} 0\\ 0 &{} {\rho _{23}^*} &{} {\rho _{33}} &{} 0\\ {\rho _{14}^*} &{} 0 &{} 0 &{} {\rho _{44}}\\ \end{array}} \right) , \end{aligned}$$

(12)

that is $\rho _{12}=\rho _{13}=\rho _{24}=\rho _{34}=0$. This visual appearance resembling the letter X has led them to be called X-state [29, 30]. Sometimes the off-diagonal elements are all real and the condition $\rho _{2,2}=\rho _{3,3}$ is satisfied, which will contribute to simplify the further calculations.

The eigenvalues and their corresponding normalized eigenvectors of the density matrix $\rho _{AB}$ in Eq. (12) are given by

$$\begin{aligned} \lambda _{1,2}= & {} \frac{(\rho _{11}+\rho _{44}) \pm \sqrt{(\rho _{11}-\rho _{44})^2+4 \, |\rho _{14}|^2}}{2}, \nonumber \\ \lambda _{3,4}= & {} \frac{(\rho _{22}+\rho _{33}) \pm \sqrt{(\rho _{22}-\rho _{33})^2+4 \, |\rho _{23}|^2}}{2}, \end{aligned}$$

(13)

and

$$\begin{aligned} \begin{aligned}&u_1=\frac{1}{N_1}\left( \begin{array}{c} \rho _{14}\\ 0\\ 0\\ \lambda _1-\rho _{11} \end{array}\right) , u_2=\frac{1}{N_2}\left( \begin{array}{c} \rho _{14}\\ 0\\ 0\\ \lambda _2-\rho _{11} \end{array}\right) ,\\&u_3=\frac{1}{N_3}\left( \begin{array}{c} 0\\ \rho _{23}\\ \lambda _3-\rho _{22}\\ 0 \end{array}\right) , u_4=\frac{1}{N_4}\left( \begin{array}{c} 0\\ \rho _{23}\\ \lambda _4-\rho _{22}\\ 0 \end{array}\right) , \end{aligned} \end{aligned}$$

(14)

where the $N_i(i=1,4)$ are the normalization factors written by

$$\begin{aligned} \begin{array}{l} N_1=\sqrt{|\rho _{14}|^2+(\lambda _1-\rho _{11})^2},\\ N_2=\sqrt{|\rho _{14}|^2+(\lambda _2-\rho _{11})^2},\\ N_3=\sqrt{|\rho _{23}|^2+(\lambda _3-\rho _{22})^2},\\ N_4=\sqrt{|\rho _{23}|^2+(\lambda _4-\rho _{22})^2}. \end{array} \end{aligned}$$

(15)

That is to say, the density matrix $\rho _{AB}$ can be diagonalized by the unitary transformation $\rho =U{\varLambda }U^{\dagger }$. The columns of the unitary matrix U are the eigenvectors of $\rho _{AB}$, and the elements of diagonal matrix ${\varLambda }$ are the corresponding eigenvalues. By straightforward calculations, the root of the two-qubit reduced state $\sqrt{\rho _{AB}}=U \sqrt{{\varLambda }} U^{\dagger }$ has the form

$$\begin{aligned} \sqrt{\rho _{AB}}=\left( {\begin{array}{*{20}c} a &{} 0 &{} 0 &{} w \\ 0 &{} b &{} z &{} 0 \\ 0 &{} z^*&{} c &{} 0 \\ w^*&{} 0 &{} 0 &{} d \\ \end{array}} \right) , \end{aligned}$$

(16)

with the elements

$$\begin{aligned} \begin{array}{l} a=|\rho _{14}|^2\left( \frac{\sqrt{\lambda _1}}{N_1^2}+\frac{\sqrt{\lambda _2}}{N_2^2}\right) ,\\ b=|\rho _{23}|^2\left( \frac{\sqrt{\lambda _3}}{N_3^2}+\frac{\sqrt{\lambda _4}}{N_4^2}\right) ,\\ c=\frac{\sqrt{\lambda _3}\left( \lambda _3-\rho _{22}\right) ^2}{N_3^2}+\frac{\sqrt{\lambda _4}\left( \lambda _4-\rho _{22}\right) ^2}{N_4^2}\\ d=\frac{\sqrt{\lambda _1}\left( \lambda _1-\rho _{11}\right) ^2}{N_1^2}+\frac{\sqrt{\lambda _2}\left( \lambda _2-\rho _{11}\right) ^2}{N_2^2},\\ w=\rho _{14}\left( \frac{\sqrt{\lambda _1}\left( \lambda _1-\rho _{11}\right) }{N_1^2}+\frac{\sqrt{\lambda _2}\left( \lambda _2-\rho _{11}\right) }{N_2^2}\right) ,\\ z=\rho _{23}\left( \frac{\sqrt{\lambda _3}\left( \lambda _3-\rho _{22}\right) }{N_3^2}+\frac{\sqrt{\lambda _4}\left( \lambda _4-\rho _{22}\right) }{N_4^2}\right) . \end{array} \end{aligned}$$

(17)