Skip to main content
SpringerLink
Log in

Differential geometric treewidth estimation in adiabatic quantum computation

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

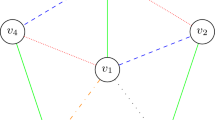
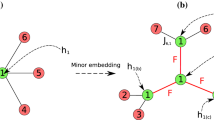
The D-Wave adiabatic quantum computing platform is designed to solve a particular class of problems—the Quadratic Unconstrained Binary Optimization (QUBO) problems. Due to the particular “Chimera” physical architecture of the D-Wave chip, the logical problem graph at hand needs an extra process called minor embedding in order to be solvable on the D-Wave architecture. The latter problem is itself NP-hard. In this paper, we propose a novel polynomial-time approximation to the closely related treewidth based on the differential geometric concept of Ollivier–Ricci curvature. The latter runs in polynomial time and thus could significantly reduce the overall complexity of determining whether a QUBO problem is minor embeddable, and thus solvable on the D-Wave architecture.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Farhi, E., Goldstone, J., Gutmann, S., Sipser, M.: Quantum computation by adiabatic evolution. arXiv:quant-ph/0001106

  2. Felzenszwalb, P.F.: Dynamic programming and graph algorithms in computer vision. IEEE Trans. Pattern Anal. Mach. Intell. 33(4), 721–740 (2011)

    Article  Google Scholar 

  3. Ronnow, T.F., et al.: Defining and detecting quantum speedup. arXiv:1401.2910

  4. Trummer, I., Koch, C.: Multiple query optimization on the D-Wave 2X adiabatic quantum computer. arXiv: 1501.06437

  5. Bunyk, P.I., Hoskinson, E., Johnson, M.W., Tolkacheva, E., Altomare, F., Berkley, A.J., Harris, R., Hilton, J.P., Lanting, T., Whittaker, J.: Architectural considerations in the design of a superconducting quantum annealing processor. arXiv: 1401.5504

  6. Choi, V.: Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process. 7, 193–209 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. Choi, V.: Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quantum Inf. Process. 10(3), 343–353 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Klymko, C., Sullivan, B.D., Humble, T.S.: Adiabatic quantum programming: minor embedding with hard faults. arXiv:1210.8395 [quant-ph]

  9. Bodlaender, H.L.: A linear-time algorithm for finding tree-decompositions of small treewidth. SIAM J. Comput. 25(6), 1305–1317 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kloks, T.: Treewidth: computations and approximations. In: No. 842 in Lecture Notes in Computer Science. Springer (1994)

  11. Robertson, N., Seymour, P.: Graph minors–XIII: the disjoint paths problem. J. Comb. Theory Ser. B 63(1), 65–110 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  12. Wu, K.J.: Solving practical problems with quantum computing hardware. In: ASCR Workshop on Quantum Computing for Science (2015)

  13. Bodlaender, H.L., Koster, A.M.C.A.: Treewidth computation II. In: Lower Bounds, Technical Report UU-CS-2010-22. Department of Information and Computing Sciences, Utrecht University (2010)

  14. Zick, K.M., Shehab, O., French, M.: Experimental quantum annealing: case study involving the graph isomorphism problem. Scientific Reports (2015). doi:10.1038/srep11168

  15. Perdomo-Ortiz, A., Fluegemann, J., Narasimhan, S., Biswas, R., Smelyanskiy, V.N.: A quantum annealing approach for fault detection and diagnosis of graph-based systems. Eur. Phys. J. Special Top. 224(1), 131–148 (2015)

    Article  ADS  Google Scholar 

  16. O’Gorman, B., Babbush, R., Perdomo-Ortiz, A., Aspuru-Guzik, A., Smelyanskiy, V.: Bayesian network structure learning using quantum annealing. Eur. Phys. J. Special Top. 224(1), 163–188 (2015)

    Article  ADS  Google Scholar 

  17. Rieffel, E.G., Venturelli, D., O’Gorman, B., Do, M.B., Prystay, E., Smelyanskiy, V.N.: A case study in programming a quantum annealer for hard operational planning problems. Quantum Inf. Process. 14(1), 1–36 (2015)

    Article  ADS  MATH  Google Scholar 

  18. Cai, J., Macready, W.G., Roy, A.: A practical heuristic for finding graph minors. arXiv:1406.2741 (2014)

  19. Wang, C., Chen, H., Jonckheere, E.: Quantum versus simulated annealing in wireless interference network optimization. Scientific Reports (2016). doi:10.1038/srep25797

  20. Adler, I., Dorn, F., Fomin, F.V., Sau, I., Thilikos, D.M.: Faster parameterized algorithms for minor containment. Theor. Comput. Sci 412(50), 7018–7028 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. King, A.D., McGeoch, C.C.: Algorithm engineering for a quantum annealing platform. arXiv:1410.2628 (2014)

  22. Ramachandramurthi, S.: The structure and number of obstructions to treewidth. SIAM J. Discrete Math. 10(1), 146–157 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  23. Berry, A., Blair, J.R.S., Heggernes, P.: Maximum cardinality search for computing minimal triangulations. In: 28th International Workshop on Graph-Theoretic Concepts in Computer Science, London, UK, pp. 1–2. Springer (2002)

  24. Koster, A.M.C.A., Bodlaender, H.L., van Hoesel, S.P.M.: Treewidth: computational experiments. Research Memoranda 001. METEOR, Maastricht (2002)

  25. Gogate, V., Dechter, R.: A complete anytime algorithm for treewidth. In: Proceedings of the 20th Conference on Uncertainty in Artificial Intelligence, Arlington, Virginia, pp. 201–208. AUAI Press (2004)

  26. Markowitz, H.M.: The elimination form of the inverse and its application to linear programming. Manag. Sci. 3, 255–269 (1957)

    Article  MathSciNet  MATH  Google Scholar 

  27. Rose, D.J., Tarjan, R.E., Lueker, G.S.: Algorithmic aspects of vertex elimination on graphs. SIAM J. Comput. 5, 266–283 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  28. Gogate, V., Dechter, R.: A complete anytime algorithm for treewidth. In: 20th Conference on Uncertainty in Artificial Intelligence (UAI) (2004)

  29. Bodlaender, H.L., Fomin, F.V., Koster, A.M.C.A.: On exact algorithms for treewidth. Technical Report UU-CS-2006-032. Utrecht University, Institute of Information and Computing Sciences (2006)

  30. Ollivier, Y.: Ricci curvature of Markov chains on metric spaces. arXiv:math/0701886 [math.PR]

  31. Ollivier, Y.: A survey of Ricci curvature for metric spaces and Markov chains. Probab. Approach Geom. 343-381, Adv. Stud. Pure Math., 57, Math. Soc. Japan, Tokyo, (2010)

  32. Jost, J., Liu, S.: Ollivier’s Ricci curvature, local clustering and curvature dimension inequalities on graphs. arXiv:1103.4037 [math.CO]

  33. Villani, C.: Optimal transport, old and new. Springer. ISBN 978-3-540-71050-9 (2009)

  34. Villani, C.: Topics in optimal transportation. In: Graduate Studies in Mathematics, vol. 58. ISBN 0-8218-3312 (2003)

  35. Wang, C., Jonckheere, E., Banirazi, R.: Wireless network capacity versus Ollivier–Ricci curvature under Heat Diffusion (HD) protocol. In: American Control Conference (ACC), pp. 3536–3541. Portland, OR, 04–06 June 2014. http://eudoxus2.usc.edu

  36. Wang, C., Jonckheere, E., Banirazi, R.: Interference constrained network control based on curvature. In: American Control Conference (ACC), pp. 6036–6041. Boston, MA, 06–08 July 2016. http://eudoxus2.usc.edu

  37. Carballosa, W., Rodrguez, J.M., Rosario, O., Sigarreta, J.M.: Gromov hyperbolicity of minor graphs. arXiv:1506.06047 (2015)

  38. Montgolfier, F., Soto, M., Viennot, L.: Treewidth and hyperbolicity of the Internet. In: 10th IEEE International Symposium on Network Computing and Applications (NCA) (2011). doi:10.1109/NCA.2011.11

  39. Lokshtanov, D.: On the complexity of computing treelength. Math. Found. Comput. Sci. 4708, 276–287 (2007)

    MathSciNet  MATH  Google Scholar 

  40. Chepoi, V., Dragan, F., Estellon, B., Habib, M., Vaxs, Y.: Diameters, centers, and approximating trees of delta-hyperbolic geodesic spaces and graphs. In: Proceedings of the Twenty-Fourth Annual Symposium on Computational Geometry, pp. 59–68. ACM

  41. Holmes, S., Rubinstein-Salzedo, S., Seiler, C.: Curvature and concentration of Hamiltonian Monte Carlo in high dimensions. arXiv:1407.1114 (2015)

  42. Ni, C.C., Lin, Y.Y., Gao, J., Gu, X.D., Saucan, E.: Ricci curvature of the Internet topology. In: INFOCOM 2015, Hong Kong (2015)

  43. Tannenbaum, A., Sander, C., Sandhu, R., Zhu, L., Kolesov, I., Reznik, E., Senbabaoglu, Y., Georgiou, T.: Graph curvature and the robustness of cancer networks. Scientific Reports (2015). doi:10.1038/srep12323

  44. Sandhu, R., Georgiou, T., Tannenbaum, A.: Market fragility, systemic risk, and Ricci curvature. arXiv:1505.05182 (2015)

  45. Rubner, Y., Tomasi, C., Guibas. L.J.: A metric for distributions with applications to image databases. In: Proceedings of the 1998 IEEE International Conference on Computer Vision, Bombay, India, pp. 59–66 (1998)

  46. Chandrana, L.S., Subramanian, C.R.: A spectral lower bound for the treewidth of a graph and its consequences. Inf. Process. Lett. 87(4), 195200 (2003)

    MathSciNet  Google Scholar 

  47. Bauer, F., Jost, J., Liu, S.: Ollivier-Ricci curvature and the spectrum of the normalized graph Laplace operator. Math. Res. Lett. 19(6), 1185–1205 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  48. Wang, C., Jonckheere, E., Brun, T.: Ollivier–Ricci curvature and fast approximation to tree-width in embeddability of QUBO problems. In: International Symposium on Communications, Control, and Signal Processing (ISCCSP), Athens, Greece, 21–23 May, pp. 639–642 (2014)

  49. van Dijk, T., van den Heuvel, J.-P., Slob, W.: Computing treewidth with LibTW. http://www.treewidth.com/docs/LibTW

  50. Jonckheere, E., Lou, M., Bonahon, F., Bryshnikov, Y.: Euclidean versus hyperbolic congestion in idealized versus experimental networks. Internet Math. 7(1), 1–27 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This research was supported by the Army Research Office (ARO) Multi University Research Initiative (MURI) Contract W911NF-11-1-0268 and by National Science Foundation (NSF) Grant CCF-1423624.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, University of Southern California, Los Angeles, CA, 90089, USA

    Chi Wang, Edmond Jonckheere & Todd Brun

Authors
  1. Chi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Edmond Jonckheere
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Todd Brun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Edmond Jonckheere.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, C., Jonckheere, E. & Brun, T. Differential geometric treewidth estimation in adiabatic quantum computation. Quantum Inf Process 15, 3951–3966 (2016). https://doi.org/10.1007/s11128-016-1394-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-016-1394-9

Keywords

Search

Navigation