Skip to main content
SpringerLink
Log in

Analytical solution and applications of three qubits in three coupled modes without rotating wave approximation

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

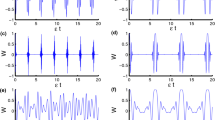
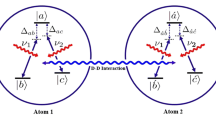
We study the dynamics of the three-qubit system interacting with multi-mode without rotating wave approximation (RWA). A physical realization of the system without direct qubits interactions with dephasing bath is proposed. It is shown that non-Markovian characters of the purity of the three qubits and the coupling strength of modes are stronger enough the RWA is no longer valid. The influences of the dephasing of qubits and interactions of modes on the dynamics of genuine multipartite entanglement and bipartite correlations of qubits are investigated. The multipartite and bipartite quantum correlations could be generated faster if we increase the coupling strength of modes and the RWA is not valid when the coupling strength is strong enough. The unitary transformations approach adopted here can be extended to other systems such as circuit or cavity quantum electrodynamic systems in the strong coupling regime.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Agarwal, G.S.: Quantum Optics. Cambridge University Press, Cambridge (2013)

    MATH  Google Scholar 

  2. Holstein, T.: Studies of polaron motion: Part I. The molecular-crystal model. Ann. Phys. 8, 325–342 (1959)

    Article  ADS  MATH  Google Scholar 

  3. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  4. Larson, J., Moya-Cessa, H.: Rabi oscillations in a quantum dot-cavity system coupled to a nonzero temperature phonon bath. Phys. Scr. 77, 065704 (2008)

    Article  ADS  MATH  Google Scholar 

  5. Zhang, J.S., Chen, A.X.: Thermal effects on bipartite and multipartite correlations in fiber coupled cavity arrays. J. Opt. Soc. Am. B 31, 1126–1131 (2014)

    Article  ADS  Google Scholar 

  6. Zhang, J.S., Chen, A.X.: Enhancement of genuine multipartite entanglement and purity of three qubits under decoherence via bang–bang pulses with finite period. Quantum Inf. Process. 15, 3257–3271 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Wu, Y., Yang, X.: Jaynes–Cummings model for a trapped ion in any position of a standing wave. Phys. Rev. Lett. 78, 3086–3088 (1997)

    Article  ADS  Google Scholar 

  8. Scully, M., Zubairy, M.S.: Quantum Optics. Cambridge University Press, Cambridge (1997)

    Book  MATH  Google Scholar 

  9. McKeever, J., Buck, J.R., Boozer, A.D., Kimble, H.J.: Determination of the number of atoms trapped in an optical cavity. Phys. Rev. Lett. 93, 143601 (2004)

    Article  ADS  Google Scholar 

  10. Hennessy, K., Badolato, A., Winger, M., Gerace, D., Atatüre, M., Gulde, S., Fält, S., Hu, E.L., Imamog brevelu, A.: Quantum nature of a strongly coupled single quantum dot-cavity system. Nature (London) 445, 896–899 (2007)

    Article  ADS  Google Scholar 

  11. Irish, E.K., Gea-Banacloche, J., Martin, I., Schwab, K.C.: Dynamics of a two-level system strongly coupled to a high-frequency quantum oscillator. Phys. Rev. B 72, 195410 (2005)

    Article  ADS  Google Scholar 

  12. Bloch, F., Siegert, A.: Magnetic resonance for nonrotating fields. Phys. Rev. 57, 522–524 (1940)

    Article  ADS  Google Scholar 

  13. Lizuain, I., Muga, J.G., Eschner, J.: Vibrational Bloch–Siegert effect in trapped ions. Phys. Rev. A 77, 053817 (2008)

    Article  ADS  Google Scholar 

  14. Sornborger, A.T., Cleland, A.N., Geller, M.R.: Superconducting phase qubit coupled to a nanomechanical resonator: beyond the rotating-wave approximation. Phys. Rev. A 70, 052315 (2004)

    Article  ADS  Google Scholar 

  15. Zueco, D., Reuther, G.M., Kohler, S., Hanggi, P.: Qubit-oscillator dynamics in the dispersive regime: analytical theory beyond the rotating-wave approximation. Phys. Rev. A 80, 033846 (2009)

    Article  ADS  Google Scholar 

  16. Chen, Q.H., Yang, Y., Liu, T., Wang, K.L.: Entanglement dynamics of two independent Jaynes–Cummings atoms without the rotating-wave approximation. Phys. Rev. A 82, 052306 (2010)

    Article  ADS  Google Scholar 

  17. Hausinger, J., Grifoni, M.: Qubit-oscillator system: an analytical treatment of the ultrastrong coupling regime. Phys. Rev. A 82, 062320 (2010)

    Article  ADS  Google Scholar 

  18. Agarwal, G.S., Rafsanjani, S.M.H., Eberly, J.H.: Tavis-Cummings model beyond the rotating wave approximation: quasidegenerate qubits. Phys. Rev. A 85, 043815 (2012)

    Article  ADS  Google Scholar 

  19. Liao, J.Q., Huang, J.F., Tian, L.: Generation of macroscopic Schrödinger-cat states in qubit-oscillator systems. Phys. Rev. A 93, 033853 (2016)

    Article  ADS  Google Scholar 

  20. Braak, D.: Integrability of the Rabi model. Phys. Rev. Lett. 107, 100401 (2011)

    Article  ADS  Google Scholar 

  21. Cárdenas, P.C., Teixeira, W.S., Semião, F.L.: Non-Markovian qubit dynamics in a circuit-QED setup. Phys. Rev. A 91, 022122 (2015)

    Article  Google Scholar 

  22. Cárdenas, P.C., Teixeira, W.S., Semião, F.L.: Coupled modes locally interacting with qubits: critical assessment of the rotating-wave approximation. Phys. Rev. A 95, 042116 (2017)

    Article  ADS  Google Scholar 

  23. Breuer, H.P., Petruccione, F.: The Theory of Open Quantum Systems. Oxford University Press, Oxford (2007)

    Book  MATH  Google Scholar 

  24. Barnett, S.M.: Quantum Information. Oxford University Press, New York (2009)

    MATH  Google Scholar 

  25. Jungnitsch, B., Moroder, T., Gühne, O.: Taming multiparticle entanglement. Phys. Rev. Lett. 106, 190502 (2011)

    Article  ADS  Google Scholar 

  26. http://www.mathworks.com/matlabcentral/fileexchange/30968

  27. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998)

    Article  ADS  MATH  Google Scholar 

  29. Yu, T., Eberly, J.H.: Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93, 140404 (2004)

    Article  ADS  Google Scholar 

  30. Yu, T., Eberly, J.H.: Sudden death of entanglement. Science (London) 323, 598–601 (2009)

    ADS  MathSciNet  MATH  Google Scholar 

  31. Zhang, J.S., Chen, A.X.: Controlling sudden transitions of bipartite quantum correlations under dephasing via dynamical decoupling. J. Phys. B At. Mol. Opt. Phys. 47, 215502 (2014)

    Article  ADS  Google Scholar 

  32. Bennett, C.H., DiVincenzo, D.P., Fuchs, C.A., Mor, T., Rains, E., Shor, P.W., Smolin, J.A., Wootters, W.K.: Quantum nonlocality without entanglement. Phys. Rev. A 59, 1070–1091 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  33. Horodecki, M., Horodecki, P., Horodecki, R., Oppenheim, J., Sen, A., Sen, U., Synak-Radtke, B.: Local versus nonlocal information in quantum-information theory: formalism and phenomena. Phys. Rev. A 71, 062307 (2005)

    Article  ADS  MATH  Google Scholar 

  34. Niset, J., Cerf, N.J.: Multipartite nonlocality without entanglement in many dimensions. Phys. Rev. A 74, 052103 (2006)

    Article  ADS  Google Scholar 

  35. Modi, K., Brodutch, A., Cable, H., Paterek, T., Vedral, V.: The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655 (2012)

    Article  ADS  Google Scholar 

  36. Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)

    Article  ADS  MATH  Google Scholar 

  37. Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A 34, 6899–6905 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Zhang, J.S., Chen, L., Abdel-Aty, M., Chen, A.X.: Sudden death and robustness of quantum correlations in the weak- or strong-coupling regime. Eur. Phys. J. D 66, 2 (2012)

    Article  ADS  Google Scholar 

  39. Ferraro, A., Aolita, L., Cavalcanti, D., Cucchietti, F.M., Acin, A.: Almost all quantum states have nonclassical correlations. Phys. Rev. A 81, 052318 (2010)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11365009 and 11065007) and the Scientific Research Foundation of Jiangxi (Grant Nos. 20151BAB202020 and 20161BBE50069).

Author information

Authors and Affiliations

  1. Department of Applied Physics, East China Jiaotong University, Nanchang, 330013, People’s Republic of China

    Jian-Song Zhang & Liu-Juan Zhang

  2. Department of Physics, Zhejiang Sci-Tech University, Hangzhou, 310018, People’s Republic of China

    Ai-Xi Chen

  3. Institute for Quantum Computing, University of Waterloo, Ontario, N2L3G1, Canada

    Ai-Xi Chen

  4. Applied Science University, Sitra, Bahrain

    Mahmoud Abdel-Aty

  5. Zewail City of Science and Technology, Giza, Egypt

    Mahmoud Abdel-Aty

  6. Sohag University, Sohag, Egypt

    Mahmoud Abdel-Aty

Authors
  1. Jian-Song Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liu-Juan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ai-Xi Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mahmoud Abdel-Aty
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ai-Xi Chen.

Appendix

Appendix

The initial state of the whole system is given in Eq. (13). In the new picture defined by \(U_j\), the initial state of the whole system is

$$\begin{aligned} |\psi '_j(0)\rangle= & {} U_j |\psi (0)\rangle = \sum _{\mu = 1}^8 d_{\mu }|\mu \rangle |\alpha _j^{(\mu )}, r_{j,a}\rangle _a |\beta _j^{(\mu )}, r_{j,b}\rangle _b |\gamma _j^{(\mu )}, r_{j,c}\rangle _c. \end{aligned}$$
(25)

The initial state of three qubits in the interaction picture defined by Eq. (11) is \(\rho ''_{j,ABC}(0) = Tr_{abc}[|\psi _j''(0)\rangle \langle \psi _j''(0)]\). The density matrix of the qubits is given by Eq. (15) with

$$\begin{aligned} \eta _{\mu \mu }= & {} 0,\quad \eta _{\nu \mu } = \eta _{\mu \nu }, \quad \eta _{18} = \eta _{27} = \eta _{36} = \eta _{45} = 3\eta \nonumber \\ \eta _{14}= & {} \eta _{16} = \eta _{17} = \eta _{23} = \eta _{25} = \eta _{28} = \eta _{35} = \eta _{38} = \eta _{46} \nonumber \\= & {} \eta _{47} = \eta _{58} = \eta _{67} = 2\eta , \nonumber \\ \eta _{12}= & {} \eta _{13} = \eta _{15} = \eta _{24} = \eta _{26} = \eta _{34} = \eta _{37} = \eta _{48} \nonumber \\= & {} \eta _{56} = \eta _{57} = \eta _{68} = \eta _{78} = \eta , \nonumber \\ f_{j,\mu \nu }(t)= & {} e^{i\varphi _{j,\mu \nu }} \langle A^{(\nu )}_{j,a}, \varepsilon _{j,a}|A^{(\mu )}_{j,a}, \varepsilon _{j,a}\rangle \langle A^{(\nu )}_{j,b}, \varepsilon _{j,b}|A^{(\mu )}_{j,b}, \varepsilon _{j,b}\rangle \langle A^{(\nu )}_{j,c}, \varepsilon _{j,c}|A^{(\mu )}_{j,c}, \varepsilon _{j,c}\rangle \qquad \quad \end{aligned}$$
(26)
$$\begin{aligned} A^{(\mu )}_{j,a}= & {} -\,\lambda ^{(\mu )}_{j,a} + e^{-i\omega _{j,a} t}\alpha _j^{(\mu )}, \quad A^{(\mu )}_{j,b} = -\lambda ^{(\mu )}_{j,b} + e^{-i\omega _{j,b} t}\beta _j^{(\mu )}, A^{(\mu )}_{j,c} = -\lambda ^{(\mu )}_{j,c}\nonumber \\&+\, e^{-i\omega _{j,c} t}\gamma _j^{(\mu )}, \nonumber \\ \alpha _j^{(\mu )}= & {} (\lambda ^{(\mu )}_{j,a} + \alpha '), \beta _j^{(\mu )} = (\lambda ^{(\mu )}_{j,b} + \beta '), \gamma _j^{(\mu )} = (\lambda ^{(\mu )}_{j,c} + \gamma '), \end{aligned}$$
(27)
$$\begin{aligned} \lambda ^{(1)}_{j,a}= & {} (a_1 + b_1 + c_1)\lambda _{j,a}, \quad \lambda ^{(2)}_{j,a} = (a_1 + b_1 - c_1)\lambda _{j,a},\nonumber \\&\lambda ^{(3)}_{j,a} = (a_1 - b_1 + c_1)\lambda _{j,a}, \end{aligned}$$
(28)
$$\begin{aligned} \lambda ^{(4)}_{j,a}= & {} (a_1 - b_1 - c_1)\lambda _{j,a}, \quad \lambda ^{(5)}_{j,a} = (-a_1 + b_1 + c_1)\lambda _{j,a},\nonumber \\&\lambda ^{(6)}_{j,a} = (-a_1 + b_1 - c_1)\lambda _{j,a},\end{aligned}$$
(29)
$$\begin{aligned} \lambda ^{(7)}_{j,a}= & {} (-a_1 - b_1 + c_1)\lambda _{j,a}, \quad \lambda ^{(8)}_{j,a} = (-a_1 - b_1 - c_1)\lambda _{j,a},\end{aligned}$$
(30)
$$\begin{aligned} \lambda ^{(1)}_{j,b}= & {} (a_2 + b_2 + c_2)\lambda _{j,b}, \quad \lambda ^{(2)}_{j,b} = (a_2 + b_2 - c_2)\lambda _{j,b},\nonumber \\&\lambda ^{(3)}_{j,b} = (a_2 - b_2 + c_2)\lambda _{j,b},\end{aligned}$$
(31)
$$\begin{aligned} \lambda ^{(4)}_{j,b}= & {} (a_2 - b_2 - c_2)\lambda _{j,b}, \quad \lambda ^{(5)}_{j,b} = (-a_2 + b_2 + c_2)\lambda _{j,b},\nonumber \\&\lambda ^{(6)}_{j,b} = (-a_2 + b_2 - c_2)\lambda _{j,b},\end{aligned}$$
(32)
$$\begin{aligned} \lambda ^{(7)}_{j,b}= & {} (-a_2 - b_2 + c_2)\lambda _{j,b}, \quad \lambda ^{(8)}_{j,b} = (-a_2 - b_2 - c_2)\lambda _{j,b},\end{aligned}$$
(33)
$$\begin{aligned} \lambda ^{(1)}_{j,c}= & {} (a_3 + b_3 + c_3)\lambda _{j,c}, \quad \lambda ^{(2)}_{j,c} = (a_3 + b_3 - c_3)\lambda _{j,c},\nonumber \\&\lambda ^{(3)}_{j,c} = (a_3 - b_3 + c_3)\lambda _{j,c},\end{aligned}$$
(34)
$$\begin{aligned} \lambda ^{(4)}_{j,c}= & {} (a_3 - b_3 - c_3)\lambda _{j,c}, \quad \lambda ^{(5)}_{j,c} = (-a_3 + b_3 + c_3)\lambda _{j,c},\nonumber \\&\lambda ^{(6)}_{j,c} = (-a_3 + b_3 - c_3)\lambda _{j,c},\end{aligned}$$
(35)
$$\begin{aligned} \lambda ^{(7)}_{j,c}= & {} (-a_3 - b_3 + c_3)\lambda _{j,c}, \quad \lambda ^{(8)}_{j,c} = (-a_3 - b_3 - c_3)\lambda _{j,c},\end{aligned}$$
(36)
$$\begin{aligned} \varepsilon _{j,a}= & {} e^{-2i\omega _{j,a} t} r_{j,a}, \quad \varepsilon _{j,b} = e^{-2i\omega _{j,b} t} r_{j,b}, \quad \varepsilon _{j,c} = e^{-2i\omega _{j,c} t} r_{j,c}, \end{aligned}$$
(37)
$$\begin{aligned} \alpha '= & {} \cos \theta _1 \alpha + \sin \theta _1 \cos \theta _2 \beta + \sin \theta _1\sin \theta _2 \gamma , \end{aligned}$$
(38)
$$\begin{aligned} \beta '= & {} -\,\sin \theta _1 \alpha + \cos \theta _1\cos \theta _2 \beta + \cos \theta _1\sin \theta _2\gamma ,\end{aligned}$$
(39)
$$\begin{aligned} \gamma '= & {} -\,\sin \theta _2\beta + \cos \theta _2 \gamma , \quad \theta _1 = \arccos \frac{1}{\sqrt{3}}, \quad \theta _2 = \pi /4. \end{aligned}$$
(40)

Here, \(|A^{(\mu )}_{j,a}, \varepsilon _{j,a}\rangle = S(\varepsilon _{j,a})D(A^{(\mu )}_{j,a}) |0\rangle \), \(|A^{(\mu )}_{j,b}, \varepsilon _{j,b}\rangle = S(\varepsilon _{j,b})D(A^{(\mu )}_{j,b}) |0\rangle \), and \(|A^{(\mu )}_{j,c}, \varepsilon _{j,c}\rangle = S(\varepsilon _{j,c})D(A^{(\mu )}_{j,c}) |0\rangle \) are the squeezed coherent states of modes a, b, and c, respectively. \(D(\alpha ) = e^{\alpha a^{\dag } - \alpha ^* a}\) and \(S(\varepsilon ) = e^{\frac{1}{2}(\varepsilon a^{\dag 2} - \varepsilon ^* a)}\) are the displacement and squeezed operators of modes.

The phase factors of \(f_{j,\mu \nu }(t)\) are as follows:

$$\begin{aligned} \varphi _{j,\mu \mu }= & {} 0, \quad \varphi _{j,12} = -t(\omega _0 + 2\xi _{j,AC} + \xi _{j,BC}) - Im(\varTheta _{j,12}), \nonumber \\ \varphi _{j,13}= & {} -\,t(\omega _0 + 2\xi _{j,AB} + 2\xi _{j,BC}) - Im(\varTheta _{j,13}),\nonumber \\&\varphi _{j,14} = -\,2t(\omega _0 + \xi _{j,AB} + \xi _{j,AC}) - Im(\varTheta _{j,14}),\nonumber \\ \varphi _{j,15}= & {} -\,t(\omega _0 + 2\xi _{j,AB} + 2\xi _{j,AC}) - Im(\varTheta _{j,15}),\nonumber \\&\varphi _{j,16} = -\,2t(\omega _0 + \xi _{j,AB} + \xi _{j,BC}) - Im(\varTheta _{j,16}),\nonumber \\ \varphi _{j,17}= & {} -\,2t(\omega _0 + \xi _{j,AC} + \xi _{j,BC}) - Im(\varTheta _{j,17}), \quad \varphi _{j,18} = -\,3\omega _0 t - Im(\varTheta _{j,18}),\nonumber \\ \varphi _{j,23}= & {} -\,2t(\xi _{j,AB} - \xi _{j,AC}) - Im(\varTheta _{j,23}), \quad \nonumber \\ \varphi _{j,24}= & {} -\,t(\omega _0 + 2\xi _{j,AB} - 2\xi _{j,BC}) - Im(\varTheta _{j,24}),\nonumber \\ \varphi _{j,25}= & {} -\,2t(\xi _{j,AB} - \xi _{j,BC}) - Im(\varTheta _{j,25}), \quad \nonumber \\ \varphi _{j,26}= & {} -\,t(\omega _0 + 2\xi _{j,AB} - 2\xi _{j,AC}) - Im(\varTheta _{j,26}),\nonumber \\ \varphi _{j,27}= & {} -\,\omega _0 t - Im(\varTheta _{j,27}), \quad \varphi _{j,28} = -2t(\omega _0 - \xi _{j,AC} - \xi _{j,BC}) - Im(\varTheta _{j,28}),\nonumber \\ \varphi _{j,34}= & {} -\,t(\omega _0 + 2\xi _{j,AC} - 2\xi _{j,BC}) - Im(\varTheta _{j,34}), \quad \nonumber \\ \varphi _{j,35}= & {} -\,2t(\xi _{j,AC} - \xi _{j,BC}) - Im(\varTheta _{j,35}), \nonumber \\ \varphi _{j,36}= & {} -\,\omega _0 t - Im(\varTheta _{j,36}), \quad \varphi _{j,37} = -t(\omega _0 - 2\xi _{j,AB} + 2\xi _{j,AC}) - Im(\varTheta _{j,37}), \nonumber \\ \varphi _{j,38}= & {} -\,2t(\omega _0 - \xi _{j,AB} - \xi _{j,BC}) - Im(\varTheta _{j,38}), \quad \varphi _{j,45} = \omega _0 t - Im(\varTheta _{j,45}), \nonumber \\ \varphi _{j,46}= & {} 2t(\xi _{j,AC} - \xi _{j,BC}) - Im(\varTheta _{j,46}), \quad \nonumber \\ \varphi _{j,47}= & {} 2t(\xi _{j,AB} - \xi _{j,BC}) - Im(\varTheta _{j,47}),\nonumber \\ \varphi _{j,48}= & {} -\,t(\omega _0 - 2\xi _{j,AB} - 2\xi _{j,AC}) - Im(\varTheta _{j,48}), \quad \nonumber \\ \varphi _{j,56}= & {} -\,t(\omega _0 - 2\xi _{j,AC} + 2\xi _{j,BC}) - Im(\varTheta _{j,56}), \nonumber \\ \varphi _{j,57}= & {} -\,t(\omega _0 - 2\xi _{j,AB} + 2\xi _{j,BC}) - Im(\varTheta _{j,57}), \quad \nonumber \\ \varphi _{j,58}= & {} -\,2t(\omega _0 - \xi _{j,AB} - \xi _{j,AC}) - Im(\varTheta _{j,58}), \nonumber \\ \varphi _{j,67}= & {} 2t(\xi _{j,AB} - \xi _{j,AC}) - Im(\varTheta _{j,67}), \quad \varphi _{j,68} \nonumber \\= & {} -\,t(\omega _0 - 2\xi _{j,AB} - 2\xi _{j,BC}) - Im(\varTheta _{j,68}), \nonumber \\ \varphi _{j,78}= & {} -\,t(\omega _0 - 2\xi _{j,AC} - 2\xi _{j,BC}) - Im(\varTheta _{j,78}),\nonumber \\ \varTheta _{j,\mu \nu }= & {} e^{i\omega _{j,a}t}\left( \lambda ^{(\mu )}_{j,a} \alpha _j^{(\mu )} - \lambda ^{(\nu )}_{j,a} \alpha _j^{(\nu )}\right) +e^{i\omega _{j,b}t}\left( \lambda ^{(\mu )}_{j,b} \beta _j^{(\mu )} - \lambda ^{(\nu )}_{j,b} \beta _j^{(\nu )}\right) \nonumber \\&+\,e^{i\omega _{j,c}t}\left( \lambda ^{(\mu )}_{j,c} \gamma _j^{(\mu )} - \lambda ^{(\nu )}_{j,c} \gamma _j^{(\nu )}\right) , \end{aligned}$$
(41)

where Im(c) is the imaginary part of complex number c.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, JS., Zhang, LJ., Chen, AX. et al. Analytical solution and applications of three qubits in three coupled modes without rotating wave approximation. Quantum Inf Process 17, 125 (2018). https://doi.org/10.1007/s11128-018-1891-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-1891-0

Keywords

Search

Navigation