Abstract
A quantum algorithm to evaluate the resiliency of a Boolean function is explored. Recently, Chakraborty and Maitra (Cryptogr Commun 8(3):401–413, 2016) have provided quantum algorithms to check the non-resiliency of a Boolean function. However, the shortage of their algorithms is that they just output YES or NO. Refining one of the algorithms, a quantum algorithm is proposed here, which can describe the extent of the non-resiliency by \(\epsilon \)-almost resiliency under the condition NO.
Similar content being viewed by others
References
Chakraborty, K., Maitra, S.: Application of Grover’s algorithm to check non-resiliency of a Boolean function. Cryptogr. Commun. 8(3), 401–413 (2016)
Li, H., Yang, L.: A quantum algorithm for approximating the influences of Boolean functions and its applications. Quantum Inf. Process. 14(6), 1787–1797 (2015)
Montanaro, A., de Wolf, R.: A Survey of Quantum Property Testing, arXiv:1310.2035v3 [quant-ph] 10 Dec (2014)
Chor, B., Goldreich, O., Hastad, J., Freidmann, J., Rudich, S., Smolensky, R.: The bit extraction problem or t-resilient functions. In: Proceedings of the 26th IEEE Symposium on Foundations of Computer Science, pp. 396–407 (1985)
Bennett, C.H., Brassard, G., Robert, J.-M.: Privacy amplification by public discussion. SIAM J. Comput. 17(2), 210–229 (1988)
Kurosawa, K., Johansson, T., Stinson, D.: Almost k-wise independent sample spaces and their applications. J. Cryptol. 14(4), 231–253 (2001)
Xiao, G.Z., Massey, J.L.: A spectral characterization of correlation-immune combining functions. IEEE Trans. Inf. Theory 34(3), 569–571 (1988)
Gopalakrishnan, K., Stinson, D.R.: Three characterizations of non-binary correlation-immune and resilient functions. Des. Codes Cryptogr. 5(3), 241–251 (1995)
Camion, P., Canteaut, A.: Correlation-immune and resilient functions over a finite alphabet and their applications in cryptography. Des. Codes Cryptogr. 16(2), 121–149 (1999)
Zhang, X.-M., Zheng, Y.: Cryptographically resilient functions. IEEE Trans. Inf. Theory 43(5), 1740–1747 (1997)
Sarkar, P., Maitra, S.: Construction of nonlinear Boolean functions with important cryptographic properties. In: Advances in Cryptology—EUROCRYPT 2000, Lecture Notes in Computer Science. Springer, pp. 485-506 (2000)
Zhang, W.G., Xiao, G.Z.: Constructions of almost optimal resilient Boolean functions on large even number of variables. IEEE Trans. Inf. Theory 55(12), 5822–5831 (2009)
Zhang, W.-G., Pasalic, E.: Generalized Maiorana–McFarland construction of resilient Boolean functions with high nonlinearity and good algebraic properties. IEEE Trans. Inf. Theory 60(10), 6681–6695 (2014)
Kurosawa, K., Matsumoto, R.: Almost security of cryptographic Boolean functions. IEEE Trans. Inf. Theory 50(11), 2752–2761 (2004)
Ke, P., Zhang, J., Wen, Q.: Results on almost resilient functions. ACNS 2006, LNCS, vol. 3989, pp. 421–432 (2006)
Canteaut, A., Carlet, C., Charpin, P., Fontaine, C.: On cryptographic properties of the cosets of R(1, m). IEEE Trans. Inf. Theory 47(4), 1494–1513 (2001)
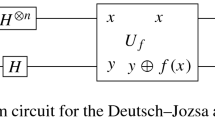
Deutsch, D., Jozsa, R.: Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. A439, 553–558 (1992)
Hoeffding, W.: Probability inequalities for sums of bounded random variables. Am. Stat. Assoc. J. 58(301), 13–30 (1963)
Bierbrauer, J., Schellwat, H.: Almost independent and weakly biased arrays: efficient constructions and cryptologic applications. CRYPTO 2000, LNCS, vol. 1880, pp. 533–543 (2000)
Acknowledgements
This work was supported by the Science and Technology Project of Henan Province (China) under Grant No. 162102210103, Natural Science foundation of Henan Province (China) 162300410191.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Proof of Lemma 1
Let \(x'\in \{x_1,\ldots , x_n\}-\{x_{i_1},\ldots , x_{i_t}\}\), then
Taking \(x_{i_1}\ldots x_{i_t}=\alpha _{i_1}\ldots \alpha _{i_t}\), we have
And hence,
Substitute (9) into (25), then we have
\(\square \)
Appendix B
Proof of Theorem 1
In addition, we have
Combined (26) with (27), we obtain
\(\square \)
Rights and permissions
About this article
Cite this article
Li, H. A quantum algorithm for testing and learning resiliency of a Boolean function. Quantum Inf Process 18, 51 (2019). https://doi.org/10.1007/s11128-018-2162-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-018-2162-9