Skip to main content
SpringerLink
Log in

Least-squares solutions to polynomial systems of equations with quantum annealing

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

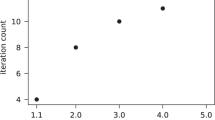
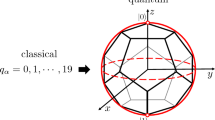
Abstract

This work proposes and analyzes a methodology for finding least-squares solutions to the systems of polynomial equations. Systems of polynomial equations are ubiquitous in computational science, with major applications in machine learning and computer security (i.e., model fitting and integer factorization). The proposed methodology maps the squared-error function for a polynomial equation onto the Ising–Hamiltonian model, ensuring that the approximate solutions (by least squares) to real-world problems can be computed on a quantum annealer even when the exact solutions do not exist. Hamiltonians for integer factorization and polynomial systems of equations are implemented and analyzed for both logical optimality and physical practicality on modern quantum annealing hardware.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Aharonov, D., Van Dam, W., Kempe, J., Landau, Z., Lloyd, S., Regev, O.: Adiabatic quantum computation is equivalent to standard quantum computation. SIAM Rev. 50(4), 755–787 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  2. Albash, T., Lidar, D.A.: Adiabatic quantum computation. Rev. Mod. Phys. 90(1), 015002 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  3. Alghassi, H., Dridi, R., Tayur, S.: Graver bases via quantum annealing with application to non-linear integer programs. arXiv preprint arXiv:1902.04215 (2019)

  4. Andriyash, E., Bian, Z., Chudak, F., Drew-Brook, M., King, A.D., Macready, W.G., Roy, A.: Boosting Integer Factoring Performance via Quantum Annealing Offsets. D-Wave White Papers, Hanover (2016)

    Google Scholar 

  5. Barahona, F.: On the computational complexity of Ising spin glass models. J. Phys. A: Math. Gen. 15(10), 3241 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  6. Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., Lloyd, S.: Quantum machine learning. Nature 549(7671), 195 (2017)

    Article  ADS  Google Scholar 

  7. Boixo, S., Rønnow, T.F., Isakov, S.V., Wang, Z., Wecker, D., Lidar, D.A., Martinis, J.M., Troyer, M.: Evidence for quantum annealing with more than one hundred qubits. Nat. Phys. 10(3), 218 (2014)

    Article  Google Scholar 

  8. Boothby, K., Bunyk, P., Raymond, J., Roy, A.: Next-generation topology of d-wave quantum processors. D-Wave White Papers 22, 28 (2018)

    Google Scholar 

  9. Borle, A., Lomonaco, S.J.: Analyzing the quantum annealing approach for solving linear least squares problems. In: International Workshop on Algorithms and Computation, pp. 289–301. Springer, Berlin (2019)

  10. Cai, J., Macready, W.G., Roy, A.: A practical heuristic for finding graph minors. arXiv preprint arXiv:1406.2741 (2014)

  11. Chang, C.C., Gambhir, A., Humble, T.S., Sota, S.: Quantum annealing for systems of polynomial equations. Sci. Rep. 9(1), 10258 (2019)

    Article  ADS  Google Scholar 

  12. Dattani, N.: Quadratization in discrete optimization and quantum mechanics. arXiv preprint arXiv:1901.04405 (2019)

  13. Dridi, R., Alghassi, H.: Prime factorization using quantum annealing and computational algebraic geometry. Sci. Rep. 7, 43048 (2017)

    Article  ADS  Google Scholar 

  14. Elgart, A., Hagedorn, G.A.: A note on the switching adiabatic theorem. J. Math. Phys. 53(10), 102202 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  15. Golub, G.H., Van Loan, C.F.: Matrix Computations, 4th edn. Johns Hopkins University Press, Baltimore (2013)

    MATH  Google Scholar 

  16. Harrow, A.W., Hassidim, A., Lloyd, S.: Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103, 150502 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  17. Jiang, S., Britt, K.A., McCaskey, A.J., Humble, T.S., Kais, S.: Quantum annealing for prime factorization. Sci. Rep. 8, 1–9 (2018)

    Article  Google Scholar 

  18. Kadowaki, T., Nishimori, H.: Quantum annealing in the transverse Ising model. Phys. Rev. E 58(5), 5355 (1998)

    Article  ADS  Google Scholar 

  19. Karimi, S., Ronagh, P.: Practical integer-to-binary mapping for quantum annealers. Quantum Inf. Process. 18(4), 94 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  20. Khoshaman, A., Vinci, W., Denis, B., Andriyash, E., Amin, M.H.: Quantum variational autoencoder. Quantum Sci. Technol. 4(1), 014001 (2018)

    Article  ADS  Google Scholar 

  21. Lasserre, J.B.: Global optimization with polynomials and the problem of moments. SIAM J. Optim. 11(3), 796–817 (2001)

    Article  MathSciNet  Google Scholar 

  22. Pakin, S.: Performing fully parallel constraint logic programming on a quantum annealer. Theory Pract. Logic Program. 18(5–6), 928–949 (2018)

    Article  MathSciNet  Google Scholar 

  23. Peng, X., Liao, Z., Xu, N., Qin, G., Zhou, X., Suter, D., Du, J.: Quantum adiabatic algorithm for factorization and its experimental implementation. Phys. Rev. Lett. 101(22), 220405 (2008)

    Article  ADS  Google Scholar 

  24. Ray, P., Chakrabarti, B.K., Chakrabarti, A.: Sherrington–Kirkpatrick model in a transverse field: absence of replica symmetry breaking due to quantum fluctuations. Phys. Rev. B 39(16), 11828 (1989)

    Article  ADS  Google Scholar 

  25. Rosenberg, I.G.: Reduction of bivalent maximization to the quadratic case. Cahiers du Centre d’etudes de Recherche Operationnelle 17, 71–74 (1975)

    MathSciNet  MATH  Google Scholar 

  26. Santoro, G.E., Martoňák, R., Tosatti, E., Car, R.: Theory of quantum annealing of an Ising spin glass. Science 295(5564), 2427–2430 (2002)

    Article  ADS  Google Scholar 

  27. Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41(2), 303–332 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  28. Steane, A.: Quantum computing. Rep. Prog. Phys. 61(2), 117 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  29. Subaşı, Y.B.U., Somma, R.D., Orsucci, D.: Quantum algorithms for systems of linear equations inspired by adiabatic quantum computing. Phys. Rev. Lett. 122, 060504 (2019)

    Article  ADS  Google Scholar 

  30. Watson, L.T., Sosonkina, M., Melville, R.C., Morgan, A.P., Walker, H.F.: Algorithm 777: Hompack90: a suite of fortran 90 codes for globally convergent homotopy algorithms. ACM Trans. Math. Softw. (TOMS) 23(4), 514–549 (1997)

    Article  MathSciNet  Google Scholar 

  31. Wen, J., Kong, X., Wei, S., Wang, B., Xin, T., Long, G.: Experimental realization of quantum algorithms for a linear system inspired by adiabatic quantum computing. Phys. Rev. A 99, 012320 (2019)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Wu-chun Feng and Mohamed W. Hassan for their council and feedback. Also, the authors would like to acknowledge the anonymous reviewers for their helpful comments, which greatly improved this paper.

Author information

Author notes

  1. Tyler H. Chang, Thomas C. H. Lux, and Sai Sindhura Tipirneni have contributed equally to this work.

Authors and Affiliations

  1. Department of Computer Science, Virginia Polytechnic Institute and State University, Blacksburg, VA, 24061, USA

    Tyler H. Chang, Thomas C. H. Lux & Sai Sindhura Tipirneni

Authors
  1. Tyler H. Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thomas C. H. Lux
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sai Sindhura Tipirneni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tyler H. Chang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chang, T.H., Lux, T.C.H. & Tipirneni, S.S. Least-squares solutions to polynomial systems of equations with quantum annealing. Quantum Inf Process 18, 374 (2019). https://doi.org/10.1007/s11128-019-2489-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-019-2489-x

Keywords

Search

Navigation