Abstract
Entanglement and coherence are quantum resources widely used in several tasks in quantum information processing. In particular, the emergence of quantum game theory arises the question whether entanglement would be more useful than coherence for quantum players. In this paper, we address such question from a two-person quantum game, namely the quantum version of the prisoner’s dilemma. We discuss the players payoffs (i) when an entangled initial game state is provided and (ii) when the system is started in a separable superposition state. As the main result, when an entangled state is provided to players, we find a situation where a non-maximally entangled state is preferable by a quantum player concerning the maximally entangled state. Thus, our first result suggests that we can establish a trade-off between maximum expected payoff and an amount of entanglement required by a quantum player. As a second result, when we provide a non-entangled initial state (but we have coherence), the payoff of a classical player is enhanced concerning the previous case. We discuss how the phase-transition-like behavior emerges from entanglement in the game considered here, so that we could design a game where no change in optimal strategies would be required.




Similar content being viewed by others
References
Meyer, D.A.: Quantum strategies. Phys. Rev. Lett. 82, 1052 (1999)
Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83, 3077 (1999)
Maioli, A., Passos, M., Balthazar, W., Souza, C., Huguenin, J., Schmidt, A.: Quantization and experimental realization of the colonel blotto game. Quantum Inf. Process. 18(1), 10 (2019)
Anand, N., Benjamin, C.: Do quantum strategies always win? Quantum Inf. Process. 14(11), 4027 (2015)
Balakrishnan, S., Sankaranarayanan, R.: Classical rules and quantum strategies in penny flip game. Quantum Inf. Process. 12(2), 1261 (2013)
Du, J., Xu, X., Li, H., Zhou, X., Han, R.: Playing prisoner’s dilemma with quantum rules. Fluct. Noise Lett. 2(04), R189 (2002)
Du, J., Li, H., Xu, X., Zhou, X., Han, R.: Entanglement enhanced multiplayer quantum games. Phys. Lett. A 302(5–6), 229 (2002)
Benjamin, S.C., Hayden, P.M.: Multiplayer quantum games. Phys. Rev. A 64, 030301 (2001)
Shi, L., Xu, F.: Nonlinear dynamics of a quantum cournot duopoly game with heterogeneous players. Quantum Inf. Process. 18(7), 227 (2019)
Mendes, R.V.: The quantum ultimatum game. Quantum Inf. Process. 4(1), 1 (2005)
Ramzan, M., Khan, M.: Distinguishing quantum channels via magic squares game. Quantum Inf. Process. 9(6), 667 (2010)
Khan, F.S., Solmeyer, N., Balu, R., Humble, T.S.: Quantum games: a review of the history, current state, and interpretation. Quantum Inf. Process. 17(11), 309 (2018)
de Ponte, M.A., Santos, A.C.: Adiabatic quantum games and phase-transition-like behavior between optimal strategies. Quantum Inf. Process. 17(6), 149 (2018)
Du, J., Li, H., Xu, X., Zhou, X., Han, R.: Phase-transition-like behaviour of quantum games. J. Phys. A: Math. Theor. 36(23), 6551 (2003)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th edn. Cambridge University Press, New York (2011)
Audenaert, K., Plenio, M.B., Eisert, J.: Entanglement cost under positive-partial-transpose-preserving operations. Phys. Rev. Lett. 90, 027901 (2003)
Plenio, M.B.: Logarithmic negativity: a full entanglement monotone that is not convex. Phys. Rev. Lett. 95, 090503 (2005)
Baumgratz, T., Cramer, M., Plenio, M.B.: Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014)
Streltsov, A., Adesso, G., Plenio, M.B.: Colloquium: quantum coherence as a resource. Rev. Mod. Phys. 89, 041003 (2017)
Gour, G., Marvian, I., Spekkens, R.W.: Measuring the quality of a quantum reference frame: the relative entropy of frameness. Phys. Rev. A 80, 012307 (2009)
Winter, A., Yang, D.: Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404 (2016)
Streltsov, A., Singh, U., Dhar, H.S., Bera, M.N., Adesso, G.: Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015)
Shao, L.H., Xi, Z., Fan, H., Li, Y.: Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 91, 042120 (2015)
Yuan, X., Zhou, H., Cao, Z., Ma, X.: Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124 (2015)
Acknowledgements
This work is supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq-Brazil). The author also acknowledges the financial support in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES) (Finance Code 001) and by the Brazilian National Institute for Science and Technology of Quantum Information [CNPq INCT-IQ (465469/2014-0)]
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Quantum coherence and phase-transition-like behavior
The phase-transition-like phenomena on optimal strategies are observed whenever we can see a discontinuous behavior of the such quantities. Let be \(\{{\$}_{A}(\lambda ),{\$}_{B}(\lambda )\}\) the expected payoff as function of some parameter \(\lambda \) for two different strategies A and B. In particular, we can define that a change in optimal expected payoff concerning the parameter \(\lambda \) is obtained when we verify

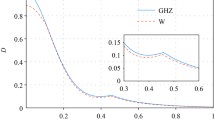
for different values (or interval) of \(\lambda _{1}\) and \(\lambda _{2}\). In fact, if  , then for the parameter \(\lambda _{1}\) the strategy A is preferable, otherwise the strategy B is preferable. Thus, the above condition allows us to identify such optimal strategy change, but it does not mean we have a phase-transition-like phenomena. We mean, if the above condition is not satisfied, we guarantee that there is no phase-transition-like phenomena, but if the condition is satisfied we need to consider a second analysis to identify the transitional behavior. In particular, this second analysis can be adopted as we done in graphs in Fig. 2.
, then for the parameter \(\lambda _{1}\) the strategy A is preferable, otherwise the strategy B is preferable. Thus, the above condition allows us to identify such optimal strategy change, but it does not mean we have a phase-transition-like phenomena. We mean, if the above condition is not satisfied, we guarantee that there is no phase-transition-like phenomena, but if the condition is satisfied we need to consider a second analysis to identify the transitional behavior. In particular, this second analysis can be adopted as we done in graphs in Fig. 2.
Now, computing the above quantities in our particular case, one gets


where we conclude that  and
and  for every \(\theta \) because \(p - r_{\mathrm{m}} >0\) \(p_{\mathrm{m}} - r >0\). From the same analysis, we have
for every \(\theta \) because \(p - r_{\mathrm{m}} >0\) \(p_{\mathrm{m}} - r >0\). From the same analysis, we have


where immediately we conclude that  for every \(\theta \). Now, let us analyze \({\$}^{U}_{\mathrm{Zino}}(\theta )\) from its maximum and minimum of the function \(\cos (4 \gamma + \theta )\) obtained when \(\theta = \theta _{\mathrm{min}} = (2 n+1) \pi - 4 \gamma \) and \(\theta = \theta _{\mathrm{max}} = 2 n \pi - 4 \gamma \), respectively. Thus, it is possible to write
for every \(\theta \). Now, let us analyze \({\$}^{U}_{\mathrm{Zino}}(\theta )\) from its maximum and minimum of the function \(\cos (4 \gamma + \theta )\) obtained when \(\theta = \theta _{\mathrm{min}} = (2 n+1) \pi - 4 \gamma \) and \(\theta = \theta _{\mathrm{max}} = 2 n \pi - 4 \gamma \), respectively. Thus, it is possible to write


Thus,  for every \(\theta \). In conclusion, in this particular situation, no phase-transition-like phenomena on optimal strategies are observed.
for every \(\theta \). In conclusion, in this particular situation, no phase-transition-like phenomena on optimal strategies are observed.
Appendix B: Complementary discussion on coherence quantifiers
In this section, we will discuss about the amount of coherence present in the initial state from alternative coherence quantifiers [19]. In general, a good coherence quantifier should satisfy six conditions as discussed in details by Streltsov, Adesso, and Plenio in their Colloquium [19]. Therefore, here we will consider the study on three different quantifiers, in which the result in Eq. (16) is also discussed here.
As a first quantifier to be considered, we write the relative entropy of coherence given by [18, 20, 21]
where \(S(\rho ) = \text {Tr}\{{\rho \log _{2} \rho }\}\) is the von Neumann entropy of the state \(\rho \) and \(\Delta [\bullet ]\) is the dephasing operation defined as [21]
with D the dimension of the system’s Hilbert space. It is important to mention here that the reference basis for quantifying coherence is \(|{\xi _{n}}\rangle \), where for our qubit such basis becomes \(|{0}\rangle \) and \(|{1}\rangle \). As a second quantifier of coherence, we consider the geometric coherence defined as [22]
where \(\chi \) is a state within the set of incoherent states \(\mathcal {I}\) given by \(\chi = \sum _{n=1}^{D} p_{i} |{\xi _{n}}\rangle |{\xi _{n}}\rangle \), with \(p_{i}\) being probabilities of getting \(|{\xi _{n}}\rangle \) after a single measurement in basis \(|{\xi _{n}}\rangle \). The norm used in the above quantity reads as \(||A||_{1} = \text {Tr}\sqrt{A^{\dagger }A}\). As shown by Streltsov et al. [22], for a single-qubit state the quantity \(C_{\mathrm{g}}(\rho )\) reads as
where \(\rho _{01} = \langle {0}|\rho |{1}\rangle \) is an off-diagonal element of \(\rho \). However, as proofed by Shao et al. [23], the above quantity does not satisfy the monotonicity condition established in [19]. Therefore, the above definition is not a good measure for quantifying coherence. However, there is a measure of coherence defined by Yuan et al. [24] given as a function \(C_{\mathrm{g}}(\rho )\) where the monotonicity condition is recovered. Thus, we have a convex roof quantifier of coherence as [24] (for a single qubit)
where \(h(x) = -x \log _{2}x - (1 - x)\log _{2}(1 - x)\). The above expression is called coherence of formation. Therefore, by using the quantifiers \(C_{\mathrm{r}}(\rho )\) and \(C_{\mathrm{f}}(\rho )\), it is possible to show that
In fact, since \(|\rho _{01}|^2 = \cos ^2 \gamma \sin ^2 \gamma \), one finds \(C_{\mathrm{g}}(\rho ) = \sin ^2 \gamma \). Thus, from the function h(x), it is straightforward to conclude that \(C_{\mathrm{f}}(\rho )\) is given by the above equation, since \(1-\sin ^2 \gamma = \cos ^2 \gamma \). On the other hand, by using that the input state of the game gives \(\Delta [\rho ] = \cos ^{2}\gamma |{0}\rangle \langle {0}| +\sin ^{2}\gamma |{1}\rangle \langle {1}|\), \(S(\rho ) = 0\) (because we have a initial pure state) and \(S(\rho ) = \sum _{n} p_{n}\rho \log _{2} p_{n}\), where \(p_{n} = \langle {n}|\rho |{n}\rangle \), it is immediate to see that \(C_{\mathrm{r}}(\rho )\) is given by the above equation. In Fig. 5, we show each quantity defined here, so that we conclude that all coherence quantifiers used here are qualitatively equivalent.
Rights and permissions
About this article
Cite this article
Santos, A.C. Entanglement and coherence in quantum prisoner’s dilemma. Quantum Inf Process 19, 13 (2020). https://doi.org/10.1007/s11128-019-2502-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-019-2502-4