Multiple-pulse phase-matching quantum key distribution

Abstract

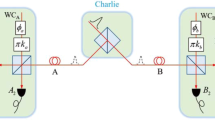
We propose a multiple-pulse phase-matching quantum key distribution protocol to exceed the linear key rate bound and to achieve higher error tolerance. In our protocol, Alice and Bob generate at first their own pulse train (each train should contain L pulses) as well as random bit sequences and also encode each pulse of their train with a randomized phase and a modulation phase. As the next step, both encoded trains are simultaneously sent to Charlie, who performs an interference detection and may be also an eavesdropper. After a successful detection is announced by Charlie, Alice and Bob open the randomized phase of each pulse and keep only communications when the summation of the difference randomized phases at two success detections’ time stamps for Alice and Bob is equal to 0 or $\pi$. Thereafter, Alice and Bob compute the sifted key with the time stamps. The above procedure is repeated until both Alice and Bob achieve sufficiently long sifted keys. We can also show that the secret key rate of the proposed QKD protocol can beat the rate-loss limit of so far known QKD protocols when the transmission distance is greater than 150–175 km. Moreover, the proposed protocol has a higher error tolerance, approximately 22.5%, when the transmission distance is 50 km and $L = 128$. The secret key rate and the transmission distance of our protocol are superior to that of the round-robin differential phase shift quantum key distribution protocol Sasaki et al. (Nature 509:475–480, 2014) and the measurement-device-independent quantum key distribution protocol Lo et al. (Phys Rev Lett 108:130503, 2012), and the secret key rate performance is better in both cases than that of phase-matching quantum key distribution when bit train length is greater than 16.

Appendices

Appendix A

The quantum states of Alice and Bob are given by

$$\begin{aligned} \frac{1}{\sqrt{L}}\sum _{m=1}^{L}e^{i(\phi _A^m+k_A^{m}\pi )}\hat{a}_{m}^{+}\mid 0>, \frac{1}{\sqrt{L}}\sum _{n=1}^{L}e^{i(\phi _B^n+k_B^{n}\pi )}\hat{b}_{n}^{+}\mid 0>. \end{aligned}$$

(A11)

respectively, where $\hat{a}_{m}^{+}, \hat{b}_{m}^{+}$ are the creation operator of Alice’s and Bob’s m-th position at a and b paths, respectively, as shown in Fig. 1. After the interference by the beam splitter which replaces $\hat{a}_{m}^{+}$ by $(\hat{c}_{m}^{+}+\hat{d}_{m}^{+})/\sqrt{2}$ and $\hat{b}_{n}^{+}$ by $(\hat{c}_{m}^{+}-\hat{d}_{n}^{+})/\sqrt{2}$, the output result becomes

$$\begin{aligned}&\left( \frac{1}{\sqrt{L}}\sum _{m=1}^{L}e^{i(\phi _A^m+k_A^{m}\pi )}\hat{a}_{m}^{+}\right) \left( \frac{1}{\sqrt{L}} \sum _{n=1}^{L}e^{i(\phi _B^n+k_B^{n}\pi )}\hat{b}_{n}^{+}\right) \nonumber \\&\quad =\left( \frac{1}{\sqrt{2L}}\sum _{m=1}^{L}e^{i(\phi _A^m+k_A^{m}\pi )}(\hat{c}_{m}^{+}+\hat{d}_{m}^{+})\right) \left( \frac{1}{\sqrt{2L}}\sum _{n=1}^{L}e^{i(\phi _B^n +k_B^{n}\pi )}(\hat{c}_{n}^{+}-\hat{d}_{n}^{+})\right) \nonumber \\&\quad =\left( \frac{1}{\sqrt{2L}}\sum _{m=1}^{L}e^{i(\phi _A^m+k_A^{m}\pi )}\hat{c}_{m}^{+}+\frac{1}{\sqrt{2L}}\sum _{m=1}^{L}e^{i(\phi _A^m+k_A^{m}\pi )} \hat{d}_{m}^{+}\right) \nonumber \\&\quad \quad \left( \frac{1}{\sqrt{2L}}\sum _{n=1}^{L}e^{i(\phi _B^n+k_B^{n}\pi )}\hat{c}_{n}^{+} -\frac{1}{\sqrt{2L}}\sum _{n=1}^{L}e^{i(\phi _B^n+k_B^{n}\pi )}\hat{d}_{n}^{+}\right) \nonumber \\&\quad =e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{c}_{1}^{+}\hat{c}_{1}^{+}+ \cdots +e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{c}_{1}^{+}\hat{c}_{L}^{+}\nonumber \\&\quad \quad -e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{c}_{1}^{+}\hat{d}_{1}^{+}- \cdots -e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{c}_{1}^{+}\hat{d}_{L}^{+} \nonumber \\&\quad \quad +e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{c}_{2}^{+}\hat{c}_{1}^{+}+ \cdots +e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{c}_{2}^{+}\hat{c}_{L}^{+} \nonumber \\&\quad \quad -e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{c}_{2}^{+}\hat{d}_{1}^{+}- \cdots -e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{c}_{2}^{+}\hat{d}_{L}^{+} \nonumber \\&\quad \quad +\cdots \nonumber \\&\quad \quad +e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{c}_{L}^{+}\hat{c}_{1}^{+}+\cdots +e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{c}_{L}^{+}\hat{c}_{L}^{+} \nonumber \\&\quad \quad -e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{c}_{L}^{+}\hat{d}_{1}^{+}-\cdots -e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{c}_{L}^{+}\hat{d}_{L}^{+} \nonumber \\&\quad \quad +e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{d}_{1}^{+}\hat{c}_{1}^{+}+\cdots +e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{d}_{1}^{+}\hat{c}_{L}^{+} \nonumber \\&\quad \quad -e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{d}_{1}^{+}\hat{d}_{1}^{+}-\cdots -e^{i(\phi _A^1+k_A^{1}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{d}_{1}^{+}\hat{d}_{L}^{+} \nonumber \\&\quad \quad +e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{d}_{2}^{+}\hat{c}_{1}^{+}+\cdots +e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{d}_{2}^{+}\hat{c}_{L}^{+} \nonumber \\&\quad \quad -e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{d}_{2}^{+}\hat{d}_{1}^{+}-\cdots -e^{i(\phi _A^2+k_A^{2}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{d}_{2}^{+}\hat{d}_{L}^{+} \nonumber \\&\quad \quad +\cdots \nonumber \\&\quad \quad +e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{d}_{L}^{+}\hat{c}_{1}^{+}+\cdots +e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{d}_{L}^{+}\hat{c}_{L}^{+} \nonumber \\&\quad \quad -e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{1}+k_B^{1}\pi )}\hat{d}_{L}^{+}\hat{d}_{1}^{+}-\cdots -e^{i(\phi _A^L+k_A^{L}\pi +\phi _B^{L}+k_B^{L}\pi )}\hat{d}_{L}^{+}\hat{d}_{L}^{+} \nonumber \\&\quad =\frac{1}{2L}\sum _{1 \le m \le L}^{}e^{i(\phi _A^m+k_A^{m}\pi +\phi _B^{m}+k_B^{m}\pi )}\hat{c}_{m}^{+}\hat{c}_{m}^{+} \nonumber \\&\quad \quad +\frac{1}{2L}\sum _{1 \le m \le L}^{}e^{i(\phi _A^{m}+k_A^{m}\pi +\phi _B^{m}+k_B^{m}\pi )}\hat{d}_{m}^{+}\hat{d}_{m}^{+} \nonumber \\&\quad \quad +\frac{1}{2L}\sum _{1 \le m< n \le L}^{}(e^{i(\phi _A^{m}+k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi )}+e^{i(\phi _A^{n}+k_A^{n}\pi +\phi _B^{m}+k_B^{m}\pi )})\hat{c}_{m}^{+}\hat{c}_{n}^{+} \nonumber \\&\quad \quad -\frac{1}{2L}\sum _{1 \le m< n \le L}^{}(e^{i(\phi _A^{m}+k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi )}+e^{i(\phi _A^{n}+k_A^{n}\pi +\phi _B^{m}+k_B^{m}\pi )})\hat{d}_{m}^{+}\hat{d}_{n}^{+} \nonumber \\&\quad \quad +\frac{1}{2L}\sum _{1 \le m< n \le L}^{}(-e^{i(\phi _A^{m}+k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi )}+e^{i(\phi _A^{n}+k_A^{n}\pi +\phi _B^{m}+k_B^{m}\pi )})\hat{c}_{m}^{+}\hat{d}_{n}^{+} \nonumber \\&\quad \quad +\frac{1}{2L}\sum _{1 \le m < n \le L}^{}(e^{i(\phi _A^{m}+k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi )}-e^{i(\phi _A^{n}+k_A^{n}\pi +\phi _B^{m}+k_B^{m}\pi )})\hat{d}_{m}^{+}\hat{c}_{n}^{+} \end{aligned}$$

(A12)

There are six items in the output result, and only the last four items are kept, since the detection results are discarded when there is only one click in the detectors. The four items’ probabilities are,

$$\begin{aligned} P(c_{m}^{+}c_{n}^{+})=<c_{m}^{+}c_{n}^{+}\mid c_{m}^{+}c_{n}^{+}>=&1+\cos (\phi _A^{m} +k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi \nonumber \\&-\phi _A^{n}-k_A^{n}\pi -\phi _B^{m}-k_B^{m}\pi ) \nonumber \\ P(c_{m}^{+}d_{n}^{+})=<c_{m}^{+}d_{n}^{+}\mid c_{m}^{+}d_{n}^{+}>=&1-\cos (\phi _A^{m} +k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi \nonumber \\&-\phi _A^{n}-k_A^{n}\pi -\phi _B^{m}-k_B^{m}\pi ) \nonumber \\ P(d_{m}^{+}c_{n}^{+})=<d_{m}^{+}c_{n}^{+}\mid d_{m}^{+}c_{n}^{+}>=&1-\cos (\phi _A^{m} +k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi \nonumber \\&-\phi _A^{n}-k_A^{n}\pi -\phi _B^{m}-k_B^{m}\pi ) \nonumber \\ P(d_{m}^{+}d_{n}^{+})=<d_{m}^{+}d_{n}^{+}\mid d_{m}^{+}d_{n}^{+}>=&1+\cos (\phi _A^{m} +k_A^{m}\pi +\phi _B^{n}+k_B^{n}\pi \nonumber \\&-\phi _A^{n}-k_A^{n}\pi -\phi _B^{m}-k_B^{m}\pi ) \end{aligned}$$

(A13)

Appendix B

Table 2 The results of detectors and the sifted key of Alice and Bob

Here, the detector results and the sifted key for Alice(Bob) when $\big |\phi _A^{m}+\phi _B^{n}-\phi _A^{n}-\phi _B^{m}\big |=0$ are listed in Table 2. The detector results are divided into two types, denoted as SAME which represents the two clicks triggered by the same detector, and DIFF which represents the two clicks triggered by different detectors.