Abstract
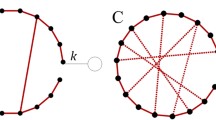
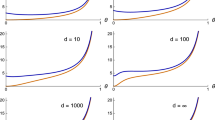
Quantum network probing is experimental estimation of network parameters by passing probes through the network. In probing with indefinite routing (IR), the probe traces a quantum mechanical superposition of different paths through the network. We consider a quantum network modeled by three identical qudit depolarizing channels, each channel with state preservation probability \(\theta \) and dimension d. Using quantum Fisher (QF) information as our measure of merit, we comprehensively assess the advantage associated with maximal IR for estimating the network depolarization rate \(1-\theta \). A three-channel network admits three distinctive types of IR, cyclical, directional, and full. Definite routing is the case where the probe is confined to a single path through the network. We find that compared to this baseline case all three IR types yield a gain in QF information, the gain being greatest with full IR. Comparing the information gains with cyclical and directional IR shows that, for \(\theta \) above a dimensional threshold, directional IR offers greater advantage, while below this threshold cyclical IR is more advantageous. Our results show further that the joint effect of cyclical IR and directional IR can be synergistic or antagonistic, depending on \(\theta \) and d. With our analytical approach, the network output states are quasi-classical, greatly simplifying the derivation of the QF information involved. This approach can be extended to larger networks with different IR schemes.






Similar content being viewed by others
Notes
The term quasi-classical is used here in the specific sense stated; it does not refer to physical modeling in the Planck limit \(h\rightarrow 0\) as, for example, in the WKB approximation [22].
The size \(\xi = \mu \lambda \) of an eigenspace is the product of its eigenvalue \(\lambda \) and its dimension \(\mu \).
The dihedral group is the abstract group of symmetries of a regular polygon, including reflections and cyclic shifts. In particular, the dihedral group \(D_3\) is the symmetry group of an equilateral triangle.
References
Kimble, H.J.: The quantum internet. Nature 453(7198), 1023–1030 (2008)
Van Meter, R.: Quantum Networking. Wiley, New York (2014)
Cirac, J.I., Zoller, P., Kimble, H.J., Mabuchi, H.: Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78(16), 3221–3224 (1997)
Proctor, T.J., Knott, P.A., Dunningham, J.A.: Multiparameter estimation in networked quantum sensors. Phys. Rev. Lett. 120(8), 080501 (2018)
Khabiboulline, E.T., Borregaard, J., De Greve, K., Lukin, M.D.: Optical interferometry with quantum networks. Phys. Rev. Lett. 123(7), 070504 (2019)
Cleve, R., Gottesman, D., Lo, H.K.: How to share a quantum secret. Phys. Rev. Lett. 83(3), 648 (1999)
Aaronson, S., Farhi, E., Gosset, D., Hassidim, A., Kelner, J., Lutomirski, A.: Quantum money. Commun. ACM 55(8), 84–92 (2012)
Cacciapuoti, A.S., Caleffi, M., Tafuri, F., Cataliotti, F.S., Gherardini, S., Bianchi, G.: Quantum internet: networking challenges in distributed quantum computing. IEEE Netw. 34(1), 137–143 (2019)
Fitzsimons, J.F.: Private quantum computation: an introduction to blind quantum computing and related protocols. Quantum Inf. 3(1), 23 (2017)
Ben-Av, R., Exman, I.: Optimized multiparty quantum clock synchronization. Phys. Rev. A 84(1), 014301 (2011)
Komar, P., Kessler, E.M., Bishof, M., Jiang, L., Sørensen, A.S., Ye, J., Lukin, M.D.: A quantum network of clocks. Nat. Phys. 10(8), 582 (2014)
Frey, M.: Indefinite causal order aids quantum depolarizing channel identification. Quantum Inf. Process. 18(4), 96 (2019)
Frey, M.: Probing the quantum depolarizing channel with mixed indefinite causal order. In: Quantum Information Science, Sensing, and Computation XI, vol. 10984, p. 109840D. International Society for Optics and Photonics (2019)
Ebler, D., Salek, S., Chiribella, G.: Enhanced communication with the assistance of indefinite causal order. Phys. Rev. Lett. 120(12), 120502 (2018)
Procopio, L.M., Delgado, F., Enríquez, M., Belabas, N., Levenson, J.A.: Communication enhancement through quantum coherent control of \(N\) channels in an indefinite causal-order scenario. Entropy 21(10), 1012 (2019)
Helstrom, C.W.: Minimum mean-squared error of estimates in quantum statistics. Phys. Lett. A 25(2), 101–102 (1967)
Tóth, G., Apellaniz, I.: Quantum metrology from a quantum information science perspective. J. Phys. A Math. Theor. 47(42), 424006 (2014)
Frey, M.R., Miller, A.L., Mentch, L.K., Graham, J.: Score operators of a qubit with applications. Quantum Inf. Process. 9(5), 629–641 (2010)
Paris, M.G.: Quantum estimation for quantum technology. Int. J. Quantum Inf. 7(supp01), 125–137 (2009)
Zhang, Y.M., Li, X.W., Yang, W., Jin, G.R.: Quantum Fisher information of entangled coherent states in the presence of photon loss. Phys. Rev. A 88(4), 043832 (2013)
Safránek, D.: Simple expression for the quantum Fisher information matrix. Phys. Rev. A 97(4), 042322 (2018)
Griffiths, D.J., Schroeter, D.F.: Introduction to Quantum Mechanics. Cambridge University Press, Cambridge (2018)
Frey, M., Collins, D., Gerlach, K.: Probing the qudit depolarizing channel. J. Phys. A Math. Theor. 44(20), 205306 (2011)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010)
King, C.: The capacity of the quantum depolarizing channel. IEEE Trans. Inf. Theory 49(1), 221–229 (2003)
Dragan, A., Wódkiewicz, K.: Depolarization channels with zero-bandwidth noises. Phys. Rev. A 71(1), 012322 (2005)
Slimen, I.B., Trabelsi, O., Rezig, H., Bouallègue, R., Bouallègue, A.: Stop conditions of BB84 protocol via a depolarizing channel (quantum cryptography). J. Comput. Sci. 3(6), 424–429 (2007)
Boixo, S., Monras, A.: Operational interpretation for global multipartite entanglement. Phys. Rev. Lett. 100(10), 100503 (2008)
Fujiwara, A.: Quantum channel identification problem. Phys. Rev. A 63(4), 042304 (2001)
Chiribella, G.: Perfect discrimination of no-signalling channels via quantum superposition of causal structures. Phys. Rev. A 86(4), 040301 (2012)
Chiribella, G., D’Ariano, G.M., Perinotti, P., Valiron, B.: Quantum computations without definite causal structure. Phys. Rev. A 88(2), 022318 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Official contribution of the National Institute of Standards and Technology; not subject to copyright in the United States.
Appendix
Appendix
This appendix shows derivations of blocks \(\mathbf {G}=\Sigma _{\text {F1},\text {B1}}\), \(\mathbf {A}=\Sigma _{\text {F1},\text {F3}}\), and \(\mathbf {B}=\Sigma _{\text {F1},\text {B3}}\) in the network outputs in (18), (25), and (32). The Kraus operators for the ith qudit depolarizing channel are \(\mathbf {D}_{i0}=\sqrt{\theta _i}\mathbf {I}\) and \(\mathbf {D}_{ij}=\frac{1}{d}\sqrt{1-\theta _i}\mathbf {U}_j\) for \(j=1,\ldots ,d^2\), where the \(\mathbf {U}_j\) are orthogonal unitary operators. Because these \(d^2\) unitary operators \(\mathbf {U}_i\) are orthogonal, they form an orthonormal basis with respect to the Hilbert–Schmidt inner product, and for any given d-dimensional linear operator \(\mathbf {V}\), we have
and
These two identities are used repeatedly in the following calculations. The notation \(\bar{\theta }_i = 1-\theta _i\) is used throughout for convenience.
Calculation of \(\mathbf {G}=\Sigma _{\text {F1},\text {B1}}\):
The three double sums in (38) are identically
while the triple sum in (38) is
Substituting (39) and (40) back into (38) then yields
with \(g_\sigma (\theta )\) and \(g_{\text {\tiny {I}}}(\theta )\) as in (19) for \(\theta _1=\theta _2=\theta _3\equiv \theta \).
Calculation of \(\mathbf {A}=\Sigma _{\text {F1},\text {F3}}\):
This yields \(a_\sigma (\theta )\) and \(a_{\text {\tiny {I}}}(\theta )\) in (26) for \(\theta _1=\theta _2=\theta _3\equiv \theta \).
Calculation of \(\mathbf {B}=\Sigma _{\text {F1},\text {B3}}\):
The four sums in (42) are
and
Substituting (43), (44), (45), and (46) back into (42) yields
with \(b_\sigma (\theta )\) and \(b_{\text {\tiny {I}}}(\theta )\) as in (33) for \(\theta _1=\theta _2=\theta _3\equiv \theta \).
Rights and permissions
About this article
Cite this article
Frey, M. Quantum network probing with indefinite routing. Quantum Inf Process 20, 13 (2021). https://doi.org/10.1007/s11128-020-02946-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-020-02946-5