Performance improvement of unidimensional continuous-variable quantum key distribution using zero-photon quantum catalysis

Abstract

Compared with symmetric Gaussian-modulated coherent state protocol, the unidimensional continuous-variable quantum key distribution (UCVQKD) only modulates one of the quadratures in phase space of coherent state, thereby simplifying its implementation. Although UCVQKD does reduce the system’s complexity, its performance is reduced. In this work, we suggest an improved approach for UCVQKD using zero-photon quantum catalysis (ZPQC) technology. By taking advantage of this non-Gaussian operation, both secret key rate and maximal transmission distance of UCVQKD can be enhanced. Moreover, compared with another well-studied non-Gaussian operation, i.e., photon subtraction, ZPQC has higher success possibility, so that it would be beneficial for improving the amount of information acquired by legitimate users. Numerical simulation shows that the performance of UCVQKD can be improved by properly applying ZPQC. In particular, we find out that the performance of ZPQC-based UCVQKD outperforms that of photon subtraction-based UCVQKD, thereby providing an alternative way to better improve UCVQKD system. Furthermore, by taking finite-size effect into account, we derive more practical secure bound of ZPQC-based UCVQKD.

Appendices

A Derivation of covariance matrixes

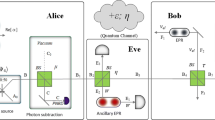
To acquire the analytical expression of security key rate, we propose the covariance matrix $\varGamma _{AB_3}$ of the inequivalent EB-based version of our scheme. Firstly, the covariance matrix of the EPR state that Alice prepared can be given by the following expression

$$\begin{aligned} \begin{aligned} \varGamma _{AB}= \begin{pmatrix} V{\mathbb {I}} &{} \sqrt{V^2-1}\sigma _z \\ \sqrt{V^2-1}\sigma _z &{} V{\mathbb {I}} \end{pmatrix} , \end{aligned} \end{aligned}$$

(10)

where ${\mathbb {I}}=diag(1, 1)$ and $\sigma _z=diag(1, -1)$. After applying ZPQC operation on mode B, the covariance matrix of the yield state $\varGamma _{AB_1}$ can be expressed as

$$\begin{aligned} \begin{aligned} \varGamma _{AB1}= \begin{pmatrix} V_A{\mathbb {I}} &{} C_1\sigma _z \\ C_1\sigma _z &{} V_{B_1}{\mathbb {I}} \end{pmatrix} , \end{aligned} \end{aligned}$$

(11)

where

$$\begin{aligned} V_A= & {} V_B=V_a+1=\frac{1+VT+V-T}{1-VT+V+T}, \end{aligned}$$

(12)

$$\begin{aligned} C_1= & {} \sqrt{T(V_A^2-1)}=\frac{2\sqrt{T(V^2-1)}}{1-VT+V+T}, \end{aligned}$$

(13)

$$\begin{aligned} V_A= & {} \frac{2\sqrt{T(V^2-1)}}{1-VT+V+T} . \end{aligned}$$

(14)

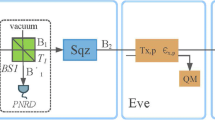
As stated above, to modulate a single quadrature x, the coherent states should be squeezed after Alice performs a heterodyne measurement on the mode A, and finally, the coherent state is sent to the trusted side, Bob. According to the EPR scheme shown in Fig. 3, the coherent states along the x quadrature can be replaced by the variance $V_M=V_A^2-1$ [24] through unidimensional modulation.

As for unidimensional protocol, the scheme can be built by two-mode squeezed vacuum state of variance $V_A$ and squeeze one of the coherent state modes with the squeezing parameter $-\log {\sqrt{V_A}}$, resulting in the following matrix:

$$\begin{aligned} \begin{aligned} \gamma _{AS}= \begin{pmatrix} V_A &{} 0 &{} C_1\sqrt{V_A} &{} 0 \\ 0 &{} V_A &{} 0 &{} -\frac{C_1}{\sqrt{V_A}} \\ C_1\sqrt{V_A} &{} 0 &{} {V_A}^2 &{} 0 \\ 0 &{} -\frac{C_1}{\sqrt{V_A}} &{} 0 &{} 1 \end{pmatrix} , \end{aligned} \end{aligned}$$

(15)

with

$$\begin{aligned} \begin{aligned} SQ= \begin{pmatrix} e^r &{} 0 \\ 0 &{} e^{-r} \end{pmatrix} = \begin{pmatrix} \sqrt{V_A} &{} 0 \\ 0 &{} \frac{1}{\sqrt{V_A}} \end{pmatrix} . \end{aligned} \end{aligned}$$

(16)

As stated above, mode A is measures by Alice using a homodyne detector and mode B is squeezed on the squeezer and sent to the channel. As the states travel through the noisy and lossy public channel, the covariance matrix is transferred to according to the channel parameters; thus, there is no modulation in the p quadrature after being squeezed by squeezer, which is defined as the ZPQC-based unidimensional modulation. Thus, the covariance matrix is redefined by the variance $V_M$ in the unidimensional modulation [24]. The covariance matrix is rewritten as follows

$$\begin{aligned} \begin{aligned} \gamma _{AB_1}= \begin{pmatrix} \sqrt{V_M+1} &{} 0 &{} C_1{(V_M+1)}^{\frac{1}{4}} &{} 0 \\ 0 &{} \sqrt{V_M+1} &{} 0 &{} C_P \\ C_1\sqrt{T_c}{(V_M+1)}^{\frac{1}{4}} &{} 0 &{} T_c(V_M+1+\chi _\mathrm{line}) &{} 0 \\ 0 &{} C_P &{} 0 &{} V_y^{B_1} \end{pmatrix} . \end{aligned} \end{aligned}$$

(17)

1.1 A.1 Asymptotic case

After transmission through the channel characterized by transmittance efficiency $T_C$ and excess noise $\epsilon _{x,y}$, the covariance matrix is written as follows

$$\begin{aligned} \begin{aligned} \gamma _{AB_1}= \begin{pmatrix} \sqrt{V_M+1} &{} 0 &{} C_1{(V_M+1)}^{\frac{1}{4}} &{} 0 \\ 0 &{} \sqrt{V_M+1} &{} 0 &{} C_P \\ C_1\sqrt{T_c}{(V_M+1)}^{\frac{1}{4}} &{} 0 &{} T_c(V_M+1+\chi _\mathrm{line}) &{} 0 \\ 0 &{} C_P &{} 0 &{} V_y^{B_1} \end{pmatrix}, \end{aligned} \end{aligned}$$

(18)

where $\chi _\mathrm{line}=\frac{1}{T_C}-1+\xi$, $C_2=\sqrt{T_C}C_1$.

In the EB scheme, the detector can be modeled as a beam splitter with transmission efficiency $\eta$, the electric noise $\xi _\mathrm{el}$ can be modeled by the state $\rho _{AB_2}$, and then, the covariance matrix $\gamma _{AB_2}$ characterizing the state $\rho _{AB}$ through the beam splitter is given by

$$\begin{aligned} \begin{aligned} \gamma _{AB_2}= \begin{pmatrix} \sqrt{V_M+1} &{} 0 &{} C_1{(V_M+1)}^{\frac{1}{4}} &{} 0 \\ 0 &{} \sqrt{V_M+1} &{} 0 &{} C_P\sqrt{\eta } \\ C_1\sqrt{T_c}{(V_M+1)}^{\frac{1}{4}} &{} 0 &{} T_c(V_M+1+\chi _\mathrm{tot}) &{} 0 \\ 0 &{} C_P\sqrt{\eta } &{} 0 &{} {\eta }V_y^{B_1}+V_N(1-\eta ) \end{pmatrix},\nonumber \end{aligned}\\ \end{aligned}$$

(19)

where $\chi _\mathrm{tot}=\chi _\mathrm{line}+\chi _\mathrm{det}$, $\chi _\mathrm{det}=(1-\eta +\xi _\mathrm{el})/\eta$ for homodyne detection.

1.2 A.2 Finite-size scenario

Following the derived results from [23], the covariance matrix of the state $\rho _{AB_3}$ can be represented as follows in the finite-size scenario

$$\begin{aligned} \begin{aligned} \gamma _{AB_3}= \begin{pmatrix} \sqrt{V_M+1} &{} 0 &{} t_mC_1{(V_M+1)}^{\frac{1}{4}} &{} 0 \\ 0 &{} \sqrt{V_M+1} &{} 0 &{} t_mC_P\sqrt{\eta } \\ t_mC_P\sqrt{\eta } &{} 0 &{} t_m^2T_c(V_M+1+\chi _\mathrm{tot})+\sigma ^2 &{} 0 \\ 0 &{} t_mC_P\sqrt{\eta } &{} 0 &{} t_m^2{\eta }V_y^{B_1}+t_m^2V_N(1-\eta )+\sigma ^2 \quad \end{pmatrix}. \end{aligned} \end{aligned}$$

(20)

Here, $t_m$ and $\sigma _m$ are the minimally estimated value of the total transmission and the maximally estimated value of the total noise. For homodyne detection, these two parameters are presented as follows

$$\begin{aligned} \begin{aligned} \sigma _m^2&=\sigma ^2+z_{\epsilon _{EP/2}}\frac{\sqrt{2}\sigma ^2}{\sqrt{m}},\\ t_m&=\sqrt{\eta T_c}-z_{\epsilon _{EP/2}}\sqrt{\frac{\sigma ^2}{mV_a}}, \end{aligned} \end{aligned}$$

(21)

where $\sigma =\eta T_c(\chi _\mathrm{line}+\chi _\mathrm{det}/T_c+1)$, $z_{\epsilon _{EP/2}}$ is such that $[1-erf(z_{\epsilon _{EP/2}}/\sqrt{2})]/2=\epsilon /2$, $\epsilon _{EP}$ is the failure probability of the parameter estimation and erf represents the error function

$$\begin{aligned} \begin{aligned} erf(x)=\frac{2}{\sqrt{\pi }}\int ^x_0e^{-t^2}dt \end{aligned}. \end{aligned}$$

(22)

B Calculation of the secret key rate

In this section, the secret key rate analysis is mainly carried out under Gaussian collective attacks, simply because they are proved to be optimal in asymptotic cases.

To obtain the lower bound of the secret key rate, the covariance matrix in the asymptotic framework thus should be derived. The secret key rate in the case of asymptotic security reads

$$\begin{aligned} \begin{aligned} K=P_Z[{\beta }I_{AB}-\chi _{BE}] \end{aligned}, \end{aligned}$$

(23)

where $\beta$ is the reconciliation efficiency, $I_{AB}$ refers to the mutual information shared by both Alice and Bob, and $\chi _{BE}$ represents the Holevo bound between Bob and Eve for reverse reconciliation. The mutual information can be derived by the following expression

$$\begin{aligned} \begin{aligned} I_{AB}=\frac{1}{2}log_2\frac{V_A}{V_{A|B_3}} \end{aligned}. \end{aligned}$$

(24)

Thus, it can be derived by the following expression under the asymptotic cases

$$\begin{aligned} \begin{aligned} I_{AB}=\frac{1}{2}log_2\frac{V_A}{V_{A|B_3}}=\frac{1}{2}log_2\frac{{\eta }T_c(V_M+1+\chi _\mathrm{tot})}{1-{\eta }T_c{C_1}^2} \end{aligned}, \end{aligned}$$

(25)

where $V_A$ is the amplitude quadrature variance for Alice, which is the first element of matrix $\gamma _A$ describing mode A, while the first diagonal element of conditional matrix $\gamma _{A|B}$, and $V_{A|B}$ which represents conditional variance in amplitude quadrature, is given by

$$\begin{aligned} \begin{aligned} \gamma _{A|x_B}=\gamma _A-\sigma _{AB}(X\gamma _BX^{-1})^{MP}{\sigma _{AB}}^T \end{aligned}, \end{aligned}$$

(26)

where MP presents the Moore–Penrose matrix inverse; $\gamma _A$, $\gamma _B$ and $\sigma _{AB}$ refer to submatrices of the covariance matrix $\gamma _{AB}$ by decomposition, namely

$$\begin{aligned} \begin{aligned} \gamma _{A|B}= \begin{pmatrix} \frac{\sqrt{V_M+1}(1-{\eta }T_c{C_1}^2)}{{\eta }T_c(V_M+1+\chi _\mathrm{tot})} &{} 0 \\ 0 &{} \sqrt{V_M+1} \end{pmatrix} , \end{aligned} \end{aligned}$$

(27)

where

$$\begin{aligned} \begin{aligned} X= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix} \end{aligned}, \end{aligned}$$

(28)

and

$$\begin{aligned} \begin{aligned} \gamma _{AB}= \begin{pmatrix} \gamma _A &{} \sigma _{AB} \\ \sigma _{AB}^T &{} \gamma _B \end{pmatrix} . \end{aligned} \end{aligned}$$

(29)

Lossy information available for Eve can be obtained by

$$\begin{aligned} \begin{aligned} \chi _{BE}=S(\rho _E)-S(\rho _E^{x_B}) \end{aligned}, \end{aligned}$$

(30)

where $S(\rho )$ is the von Neumann entropy of the quantum state $\rho$. The calculation of symplectic eigenvalues of covariance matrix $\gamma$ is applied to evaluate entropy for an n-mode Gaussian state describing $\rho$ as follows

$$\begin{aligned} \begin{aligned} S(\rho )=\sum _{i=1}^2G(\frac{(\lambda _i-1)}{2})-G(\frac{(\lambda _3-1)}{2}) \end{aligned}, \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{aligned} G(X)=(x+1)log_2(x+1)-xlog_2x \end{aligned}, \end{aligned}$$

(32)

the symplectic eigenvalues $\lambda _1$, $\lambda _2$ are given by the square roots of equation using the following equation

$$\begin{aligned} \begin{aligned} z^2-\varDelta {z}+det\gamma _B=0 \end{aligned}. \end{aligned}$$

(33)

Therefore, $\lambda _{1,2}^2$ can be calculated by the equation

$$\begin{aligned} \begin{aligned} \lambda _{1,2}^2=\frac{1}{2}[\varDelta \pm \sqrt{\varDelta ^2-4det\gamma _B}] \end{aligned}, \end{aligned}$$

(34)

where

$$\begin{aligned} \begin{aligned} \varDelta =det{\gamma _A}^2+det{\gamma _B}^2-det{\sigma _{AB}}^2 \end{aligned}, \end{aligned}$$

(35)

namely

$$\begin{aligned} \begin{aligned} \varDelta =V_M+1+V_{B_3}^2-2C_3^2 \end{aligned}, \end{aligned}$$

(36)

where $\gamma _A$, $\gamma _B$ and $\sigma _{AB}$ have been given above.

Since $S(\rho _E^{x_B})=G(\frac{\lambda _3-1}{2})$, we can calculate S(B|A) using

$$\begin{aligned} \begin{aligned} \lambda _3=\sqrt{det\gamma _{A|x_B}} \end{aligned}. \end{aligned}$$

(37)

Thus, $\lambda _3$ is calculated by

$$\begin{aligned} \begin{aligned} \lambda _3^2=\sqrt{V_M+1}\{\sqrt{V_M+1}-\frac{{C_1}^2{\eta }{T_c}\sqrt{V_M+1}}{{\eta }T_c(V_M+1+\chi _\mathrm{tot})}\} \end{aligned}. \end{aligned}$$

(38)

Besides, in the finite-size scenario, the secret key rate is given by [23]

$$\begin{aligned} \begin{aligned} K=P_Z\cdot \frac{n}{N}[\beta I_{AB}-\chi _{BE}-\varDelta (n)] \end{aligned}, \end{aligned}$$

(39)

where N refers to the total exchanged information, n is the data employed for generating low raw key ($m=N-n$) and $\varDelta (n)$ is a parameter related to privacy amplification and is given by

$$\begin{aligned} \begin{aligned} \varDelta (n)=7\sqrt{\frac{log_2(1/{\overline{\epsilon }})}{n}}+\frac{2}{n}log_2(1/\epsilon _PA) \end{aligned}, \end{aligned}$$

(40)

where ${\overline{\epsilon }}$ is a smoothing parameter and $\epsilon _{PA}$ represents the failure probability of the privacy amplification procedure. Similarly, the calculation of $I_{AB}$ and $\chi _{BE}$ is identical by replacing $C_3$ and $V_{B_3}$.