Abstract
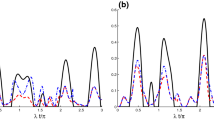
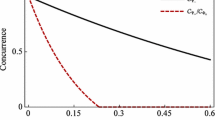
We introduce a unitary operator which may be constructed conveniently by exploiting the properties of the Glauber displacement and parity operators. We show that it can be considered as a constant of motion of a quantum system including pure dephasing interaction of a central qubit with a nano-mechanical resonator. Using the eigenvectors of the Glauber displacement operator, we paves a way for an extensive study of the dynamics of resonator-qubit states. In addition, we show that the establishment of such a constant of motion, which includes the parity operator, provides a way to introduce a capable mechanical framework to generate some desired mechanical state as superposition of the Glauber coherent states. We investigate nonclassical properties of the generated mechanical states, by evaluating mechanical-squeezing, Wigner function, position–momentum entropic squeezing, and entanglement between spin-mechanical modes. Furthermore, the pairwise classical and quantum correlations are derived based on a necessary and sufficient condition for the zero-discord state. Finally, in order to study the mechanical state’s behavior in an environment, we consider that the output state is subject to amplitude (phase)-damping channels and their dissipative properties are analyzed.









Similar content being viewed by others
Notes
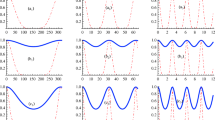
It should be noted that in order to avoid long mathematical calculations, only the calculations related to the evolved state vector and the corresponding density matrix of the system by considering the state \(|\Psi \rangle _{\lambda _{1}}\) as an initial state will be obtained in more detail. For the next three cases, we will suffice to mention the results of the calculations by presenting the form of the concurrence measure.
References
Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47(10), 777 (1935)
Schrödinger, E.: Discussion of probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 31(4), 555 (1935)
Schrödinger, E.: Probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 32(3), 446 (1936)
Horne, M.A., Shimony, A., Zeilinger, A.: Two-particle interferometry. Phys. Rev. Lett. 62, 2209 (1989)
Sanders, B.C.: Entangled coherent states. Phys. Rev. A 45, 6811 (1992)
Wang, X., Sanders, B.C.: Multipartite entangled coherent states. Phys. Rev. A 65, 012303 (2001)
Fakhri, H., Dehghani, A.: Coherency of \(su(1,1)\)-Barut–Girardello type and entanglement for spherical harmonics. J. Math. Phys. 50, 052104 (2009)
Afshar, D., Anbaraki, A.: Nonclassical properties and entanglement of superposition of two-mode separable nonlinear coherent states. J. Opt. Soc. Am. B 33, 558 (2016)
Karimi, A.: Two-mode photon-added entangled coherent-squeezed states: their entanglement and nonclassical properties. Appl. Phys. B 123, 181 (2017)
Kwiat, P.G., Mattle, K., Weinfurter, H., Zeilinger, A., Sergienko, A.V., Shih, Y.: New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337 (1995)
Pan, J.-W., Chen, Z.-B., Lu, C.-Y., Weinfurter, H., Zeilinger, A., Zukowski, M.: Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84, 777 (2012)
Karimi, E., Leach, J., Slussarenko, S., Piccirillo, B., Marrucci, L., Chen, L., She, W., Franke-Arnold, S., Padgett, M.J., Santamato, E.: Spin–orbit hybrid entanglement of photons and quantum contextuality. Phys. Rev. A 82, 022115 (2010)
Leach, J., Jack, B., Romero, J., Jha, A.K., Yao, A.M., Franke-Arnold, S., Ireland, D.G., Boyd, R.W., Barnett, S.M., Padgett, M.J.: Quantum correlations in optical angle-orbital angular momentum variables. Science 329, 662 (2010)
Bhatti, D., Zanthier, J., Agarwal, G.S.: Entanglement of polarization and orbital angular momentum. Phys. Rev. A 91, 062303 (2015)
Hach, E.E., Birrittellla, E.E., Alsing, P.M., Gerry, C.C.: SU(1,1) parity and strong violations of a Bell inequality by entangled Barut–Girardello coherent states. JOSAB 35, 2433 (2018)
Lahaye, M.D., Buu, O., Camarota, B., Schwab, K.C.: Approaching the quantum limit of a nanomechanical resonator. Science 304, 74 (2004)
Bradaschia, C., et al.: The VIRGO project: a wide band antenna for gravitational wave detection. Phys. Res. A 289, 518 (1990)
Aspelmeyer, M., Kippenberg, T.J., Marquardt, F.: Cavity optomechanics. Rev. Mod. Phys. 86, 1391 (2014)
Walter, S., Marquardt, F.: Dynamical gauge fields in optomechanics. New J. Phys. 18, 113029 (2016)
Marshall, W., Simon, C., Penrose, R., Bouwmeester, D.: Towards quantum superpositions of a mirror. Phys. Rev. Lett. 91, 130401 (2003)
O’Connell, A.D., Hofheinz, M., Ansmann, M., Bialczak, Radoslaw C., Erik Lucero, L., Neeley, M., Sank, D., Wang, H., Weides, M., Wenner, J., Martinis, J.M., Cleland, A.N.: Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697 (2010)
Chauhan, A.K., Biswas, A.: Atom-assisted quadrature squeezing of a mechanical oscillator inside a dispersive cavity. Phys. Rev. A 94, 023831 (2016)
Lu, X.-Y., Liao, J.-Q., Tian, L., Nori, F.: Steady-state mechanical squeezing in an optomechanical system via duffing nonlinearity. Phys. Rev. A 91, 013834 (2015)
Liao, J.-Q., Law, C.K.: Parametric generation of quadrature squeezing of mirrors in cavity optomechanics. Phys. Rev. A 83, 033820 (2011)
Kerdoncuff, H., Hoff, U.B., Harris, G.I., Bowen, W.P., Andersen, U.L.: Squeezing–enhanced measurement sensitivity in a cavity optomechanical system. Ann. Phys. 527, 107 (2015)
Ying, L., Lai, Y.C., Grebogi, C.: Quantum manifestation of a synchronization transition in optomechanical systems. Phys. Rev. A 90, 053810 (2014)
Teufel, J.D., Donner, T., Dale, L., Harlow, J.W., Allman, M.S., Cicak, K., Sirois, A.J., Whittaker, J.D., Lehnert, K.W., Simmonds, R.W.: Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359 (2011)
Chan, J., Alegre, T.M., Safavi-Naeini, A.H., Hill, J.T., Krause, A., Groblacher, S., Aspelmeyer, M., Painter, O.: Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89 (2011)
Verhagen, E., Deleglise, S., Weis, S., Schliesser, A., Kippenberg, T.J.: Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 482, 63 (2012)
Arcizet, O., Jacques, V., Siria, A., Poncharal, P., Vincent, P., Seidelin, S.: A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 7, 879 (2011)
Kolkowitz, S., Bleszynski Jayich, A.C., Unterreithmeier, Q.P., Bennett, S.D., Rabl, P., Harris, J.G.E., Lukin, M.D.: Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603 (2012)
LaHaye, M.D., Suh, J., Echternach, P.M., Schwab, K.C., Roukes, M.L.: Nanomechanical measurements of a superconducting qubit. Nature 459, 960 (2009)
Pirkkalainen, J.-M., Cho, S.U., Jian, L., Paraoanu, G.S., Hakonen, P.J., Sillanpää, M.A.: Hybrid circuit cavity quantum electrodynamics with a micromechanical resonator. Nature 494, 211 (2013)
Asadian, A., Brukner, C., Rabl, P.: Probing macroscopic realism via Ramsey correlation measurements. Phys. Rev. Lett. 112, 190402 (2014)
Dehghani, A., Mojaveri, B., Vaez, M.: Spin-bath dynamics in a quantum resonator-qubit system: effect of a mechanical resonator coupled to a central qubit. Int. J. Theor. Phys. 59, 3107 (2020)
Flühmann, C., Negnevitsky, V., Marinelli, M., Home, J.P.: Sequential modular position and momentum measurements of a trapped ion mechanical oscillator. Phys. Rev. X 8, 021001 (2018)
Wen-Ju, G., Yi, Z., Sun, L.-H., Yan, Y.: Generation of mechanical squeezing and entanglement via mechanical modulations. Opt. Exp. 26, 30773 (2018)
Wang, D.-Y., Bai, C.-H., Wang, H.-F., Zhu, A.-D., Zhang, S.: Steady-state mechanical squeezing in a double-cavity optomechanical system. Sci. Rep. 6, 38559 (2016)
Huang, S., Chen, A.: Mechanical squeezing in a dissipative optomechanical system with two driving tones. Phys. Rev. A 103, 023501 (2021)
Hudson, R.L.: When is the Wigner quasi-probability density non-negative? Rep. Math. Phys. 6, 249 (1974)
Kenfack, A., Zyczkowski, K.: Negativity of the Wigner function as an indicator of non-classicality. J. Opt. B Quant. Semiclass. Opt. 6, 396 (2004)
Scully, M.O., Zubairy, M.S.: Quantum Optics. Cambridge University Press, Cambridge (1997)
Dynkin, E.B.: Calculation of the coefficients in the Campbell–Hausdorff formula. Doklady Akademii Nauk SSSR 57, 323 (1947). (in Russian)
Casas, F., Murua, A., Nadinic, M.: Efficient computation of the Zassenhaus formula. Comput. Phys. Commun. 183, 2386 (2012)
Wootters, W.K.: Entanglement of formation and concurrence. Quantum Inf. Comput. 1, 27 (2001)
Hill, S., Wootters, W.K.: Entanglement of a pair of quantum bits. Phys. Rev. Lett. 78, 5022 (1997)
Wootters, W.K.: Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998)
Zhou, T., Cui, J., Long, G.L.: Measure of nonclassical correlation in coherence-vector representation. Phys. Rev. A 84, 062105 (2011)
Orlowski, A.: Information entropy and squeezing of quantum fluctuations. Phys. Rev. A 56, 2545 (1997)
Beckner, W.: Inequalities in Fourier analysis. Ann. Math. 102, 159 (1975)
Bialynicki-Birula, I., Mycielski, J.: Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 44, 129 (1975)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Derivation of time evolution operator (2)
Appendix: Derivation of time evolution operator (2)
The time evolution operator associated with the Hamiltonian (1) is given by
Defining the operators \(A:=-i\omega \tau a^{\dag }a\) and \(B=\frac{\omega }{2} \tau (a-a^{\dag })\sigma _{z}\), using the Zassenhaus formula [44], i.e.
and applying the commutation relations:
the time evolution operator U(t) can be recast into
Now, using the Baker–Campbell–Hausdorff (BCH) formula [43], i.e.
one can show that:
By exploiting the above relations, the time evolution operator U(t) gets
where we set \(\eta =e^{-i\omega \tau }-1\) and \(f(t)=-\frac{(i\omega \tau )^2}{2*2!}-\frac{(\omega \tau )^3}{2*3!}-i\frac{(\omega \tau )^{3}}{4}\left( 1+\frac{(\omega \tau )^{2}}{3!}\right) +\cdots \)
Rights and permissions
About this article
Cite this article
Dehghani, A., Mojaveri, B. & Aryaie, M. Entanglement dynamics of a nano-mechanical resonator coupled to a central qubit. Quantum Inf Process 21, 45 (2022). https://doi.org/10.1007/s11128-021-03372-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-021-03372-x