Effective quantum channel for minimum error discrimination

Abstract

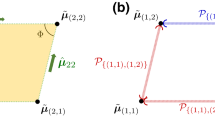
In this study, we consider a quantum channel that may help to discriminate quantum states, by which we may provide the solution for the unsolved problem of discrimination of quantum states. For the quantum channel to help the problem of discriminating given quantum states, the quantum channel should not change the guessing probability as well as the optimal measurement in minimum error discrimination of those quantum states. Therefore, we investigate a quantum channel that preserves an optimal measurement and the guessing probability with minimum error discrimination of quantum states. Then, we show that the channel does not exist in every set of quantum states but does exist when the channel and an optimal measurement commute with each other. The effectiveness of the channel can be shown more explicitly when the discrimination of linearly independent quantum states, which has not been solved yet, is considered. When we apply the channel to linearly independent quantum states, the discrimination of quantum states can be transformed into a problem in which the number of quantum states in discrimination is reduced, and we can provide a means of obtaining an answer to an unsolved quantum state discrimination. As an unsolved problem of discrimination of quantum states, we consider an ensemble of three pure states with real coefficients, whose subsets contain Unitary symmetry-called partial symmetry. By applying our strategy, we can provide an analytic result for optimal discrimination to the ensemble of three pure states with partial symmetry.

Appendix

Lemma 4

When T is the transpose with respect to a basis of $\mathcal {H}$, if an ensemble $\{p_i,\rho _i\}_{i=0}^{n-1}$ satisfies $\rho _i^T=\rho _i$ for all i and $\{M_i\}_{i=0}^{n-1}$ is the optimal POVM, then $\{M_i'=(M_i+M_i^T)/2\}_{i=0}^{n-1}$ is the other optimal POVM.

Proof

Suppose that $\{p_i,\rho _i\}_{i=0}^{n-1}$ is an ensemble composed of quantum states satisfying $\rho _i^T=\rho _i \ (\forall i)$ and $\{M_i\}_{i=0}^{n-1}$ is an optimal POVM. Then, $\{M_i^T\}_{i=0}^{n-1}$ is trivially the other optimal POVM. This is because the following relations hold:

$$\begin{aligned} \sum _{j=0}^{n-1}p_j\rho _jM_j^T-p_i\rho _i= & {} \left[ \sum _{j=0}^{n-1} p_j M_j \rho _i - p_i \rho _i \right] ^T=\left[ \sum _{j=0}^{n-1}p_j\rho _j M_j - p_i \rho _i \right] ^T\\ {}\ge & {} 0, ~ \mathrm{{for\,all }}\;i\in \{0,...,n-1\}. \end{aligned}$$

The second equality holds by the hermiticity of the symmetry operator $\sum _{j=0}^{n-1}p_j\rho _{j}M_{j}$. The third inequality holds under the optimal condition (7). A convex combination of optimal POVMs is also an optimal POVM and $\{M_i'=(M_i+M_i^T)/2\}_{i=0}^{n-1}$ satisfying $M_i'^T=M_i'$ for all i is the other optimal POVM. $\square$

When is a pure state ensemble composed of linearly independent vector , if every coefficient is real with respect to an orthonormal basis $\mathcal {B}$ of $\mathcal {H}$, the transpose T of $\mathcal {B}$ cannot affect , which suggests . Then, if $\phi _{i}$ is an optimal measurement vector, the optimal measurement of is unique and holds by the following lemma. This implies that every entry of is real. Therefore, every coefficient of with respect to $\mathcal {B}$ can be chosen as a real number. The following corollary summarizes this result.

Corollary 2

When is a pure state ensemble composed of n linearly independent vectors in $\mathcal {H}$, if every coefficient of with respect to an orthonormal basis $\mathcal {B}$ of $\mathcal {H}$, then every coefficient of the optimal measurement vectors can be chosen as a real number.

Lemma 5

Let $\mathcal {E}=\{p_i,\psi _i \}_{i=0}^{2}$ be an linearly independent pure states ensemble satisfying $U^2=I$, , and for some unitary operator U. Suppose that is the optimal measurement of MD for $\mathcal {E}$. Then holds.

Proof

Because $\textbf{M}$ is the optimal measurement, the guessing probability can be rewritten as . In addition, based on the facts that U is an unitary operator $(U^\dagger U=I)$ and it preserves trace value $(\text {Tr} \left( {UAU^\dagger } \right) =\text {Tr} \left( {A} \right) )$, then

From the given condition, we obtain

(35)

Thus

(36)

When we define $\textbf{N}=\{N_i\}_{i=0}^2$ (, , and ), they satisfy the positivity and the completeness, which implies that they form POVM. In addition, the above relations imply that $\textbf{N}$ is the optimal measurement for the MD of $\mathcal {E}=\{p_i,\psi _i\}_{i=0}^2$. Because the fact that the optimal measurement for the MD of linearly independent pure states is unique, holds. Therefore . $\square$