Polarization and orbital angular momentum coupling for high-dimensional measurement-device-independent quantum key distribution protocol

Abstract

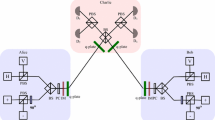
Measurement-device-independent quantum key distribution (MDI-QKD) provides an effective approach to remove all detector side channel attacks. MDI-QKD only contains one bit of information for a photon in two-dimensional space, thus performing poorly in information capacity. In contrast, the amount of information increases logarithmically in high-dimensional quantum key distribution, and multi-degree-of-freedom coupling is a feasible option. In this paper, we propose a high-dimensional measurement-device-independent quantum key distribution protocol based on polarization and orbital angular momentum coupling. We illustrate the feasibility with protocol details, deduce and simulate the secure key rate and quantum bit error rate (QBER). The simulations show that the key generation rate and the upper bound of QBER are higher compared to the standard two-dimensional case.

Appendices

Appendix A: Analysis of Bell state $\vert {\Psi }_i^\pm \rangle$ and response results

In this case, we choose $\vert {\Psi }_1^\pm \rangle$ and $\vert {\Psi }_2^\pm \rangle$ as examples for analysis. The communicating parties send $\left| 0 \right\rangle$ and $\left| 1 \right\rangle$; $\left| 2 \right\rangle$ and $\left| 3 \right\rangle$ in Z-basis, $\left| \varphi _0\right\rangle$ and $\left| \varphi _1\right\rangle$; $\left| \varphi _2\right\rangle$ and $\left| \varphi _3\right\rangle$ in X-basis. The expression of the output state is as follows:

$$\begin{aligned}{} & {} \begin{aligned} \left| \psi \right\rangle _{01}&=\frac{1}{\sqrt{2}} \left[ \left| 0 \right\rangle _{1} \otimes \left( {i\left| n \right\rangle _{1}} +\left| s \right\rangle _{1}\right) \right] \otimes \frac{1}{\sqrt{2}}\left[ \left| 1 \right\rangle _{2} \otimes \left( {i\left| n \right\rangle _{2}} +\left| s \right\rangle _{2}\right) \right] \\&=\frac{1}{2} \left( \left| 0 \right\rangle _{1} \otimes \left| 1 \right\rangle _{2} \right) \otimes \left( {i\left| n \right\rangle _{1}\left| n \right\rangle _{2} - \left| n \right\rangle _{1}\left| s \right\rangle _{2} + \left| n \right\rangle _{2}\left| s \right\rangle _{1} + i\left| s \right\rangle _{1}\left| s \right\rangle _{2}} \right) \\ \left| \psi \right\rangle _{23}&=\frac{1}{\sqrt{2}}\left[ \left| 2 \right\rangle _{1} \otimes \left( {i\left| n \right\rangle _{1}} +\left| s \right\rangle _{1}\right) \right] \otimes \frac{1}{\sqrt{2}}\left[ \left| 3 \right\rangle _{2} \otimes \left( {i\left| n \right\rangle _{2}} +\left| s \right\rangle _{2}\right) \right] \\&=\frac{1}{2} \left( \left| 2 \right\rangle _{1} \otimes \left| 3 \right\rangle _{2} \right) \otimes \left( {i\left| n \right\rangle _{1}\left| n \right\rangle _{2} - \left| n \right\rangle _{1}\left| s \right\rangle _{2} + \left| n \right\rangle _{2}\left| s \right\rangle _{1} + i\left| s \right\rangle _{1}\left| s \right\rangle _{2}} \right) \end{aligned} \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \begin{aligned} \left| \psi \right\rangle _{\phi _{0}\phi _{1}}&=\frac{1}{\sqrt{2}}\left[ \left| \varphi _0\right\rangle _{1} \otimes \left( {i\left| n \right\rangle _{1}} +\left| s \right\rangle _{1}\right) \right] \otimes \frac{1}{\sqrt{2}}\left[ \left| \varphi _1\right\rangle _{2} \otimes \left( {i\left| n \right\rangle _{2}} +\left| s \right\rangle _{2}\right) \right] \\&=\frac{1}{4} \left( \left| 0 \right\rangle _{1} \otimes \left| 1 \right\rangle _{2} + \left| 2 \right\rangle _{1}\otimes \left| 3 \right\rangle _{2} + \left| 0 \right\rangle _{2}\otimes \left| 1 \right\rangle _{1} + \left| 2 \right\rangle _{2}\otimes \left| 3 \right\rangle _{1} \right) \\&\otimes \left( {i\left| n \right\rangle _{1}\left| n \right\rangle _{2} - \left| n \right\rangle _{1}\left| s \right\rangle _{2} + \left| n \right\rangle _{2}\left| s \right\rangle _{1} + i\left| s \right\rangle _{1}\left| s \right\rangle _{2}} \right) \\ \left| \psi \right\rangle _{\phi _{2}\phi _{3}}&=\frac{1}{\sqrt{2}}\left[ \left| \varphi _2\right\rangle _{1} \otimes \left( {i\left| n \right\rangle _{3}} +\left| s \right\rangle _{1}\right) \right] \otimes \frac{1}{\sqrt{2}}\left[ \left| \varphi _1\right\rangle _{2} \otimes \left( {i\left| n \right\rangle _{2}} +\left| s \right\rangle _{2}\right) \right] \\&=\frac{1}{4} \left( \left| 1 \right\rangle _{1} \otimes \left| 0 \right\rangle _{2} + \left| 3 \right\rangle _{1}\otimes \left| 2 \right\rangle _{2} + \left| 1 \right\rangle _{2}\otimes \left| 0 \right\rangle _{1} + \left| 3 \right\rangle _{2}\otimes \left| 2 \right\rangle _{1} \right) \\&\otimes \left( {i\left| n \right\rangle _{1}\left| n \right\rangle _{2} - \left| n \right\rangle _{1}\left| s \right\rangle _{2} + \left| n \right\rangle _{2}\left| s \right\rangle _{1} + i\left| s \right\rangle _{1}\left| s \right\rangle _{2}} \right) \end{aligned} \end{aligned}$$

(A2)

where the corner markers denote the choice of quantum state for Alice and Bob. Based on the above equations, the detectors click results of HD-MDI-QKD can be analyzed. This corresponds to detectors clicks for different terms as shown in Table 5. The quantum state collapses to the following Bell states:

$$\begin{aligned} \begin{aligned}&\left| H\right\rangle \left| l\right\rangle _{1} \otimes \left| H\right\rangle \left| -l\right\rangle _{2} + \left| H\right\rangle \left| -l\right\rangle _{1} \otimes \left| H\right\rangle \left| l\right\rangle _{2} + \left| V\right\rangle \left| l\right\rangle _{1} \otimes \left| V\right\rangle \left| -l\right\rangle _{2}\\&\quad + \left| V\right\rangle \left| -l\right\rangle _{1} \otimes \left| V\right\rangle \left| l\right\rangle _{2}\\&\left| H\right\rangle \left| l\right\rangle _{1} \otimes \left| H\right\rangle \left| -l\right\rangle _{2} + \left| H\right\rangle \left| -l\right\rangle _{1} \otimes \left| H\right\rangle \left| l\right\rangle _{2} - \left| V\right\rangle \left| l\right\rangle _{1} \otimes \left| V\right\rangle \left| -l\right\rangle _{2}\\&\quad - \left| V\right\rangle \left| -l\right\rangle _{1} \otimes \left| V\right\rangle \left| l\right\rangle _{2}\\&\left| H\right\rangle \left| l\right\rangle _{1} \otimes \left| H\right\rangle \left| -l\right\rangle _{2} - \left| H\right\rangle \left| -l\right\rangle _{1} \otimes \left| H\right\rangle \left| l\right\rangle _{2} + \left| V\right\rangle \left| l\right\rangle _{1} \otimes \left| V\right\rangle \left| -l\right\rangle _{2} \\&\quad - \left| V\right\rangle \left| -l\right\rangle _{1} \otimes \left| V\right\rangle \left| l\right\rangle _{2}\\&\left| H\right\rangle \left| l\right\rangle _{1} \otimes \left| H\right\rangle \left| -l\right\rangle _{2} - \left| H\right\rangle \left| -l\right\rangle _{1} \otimes \left| H\right\rangle \left| l\right\rangle _{2} - \left| V\right\rangle \left| l\right\rangle _{1} \otimes \left| V\right\rangle \left| -l\right\rangle _{2} \\&\quad + \left| V\right\rangle \left| -l\right\rangle _{1} \otimes \left| V\right\rangle \left| l\right\rangle _{2} \end{aligned} \end{aligned}$$

(A3)

Table 5 Detector clicks for different terms

The former (later) two items correspond to $\vert {\Psi }_1^\pm \rangle$ ($\vert {\Psi }_2^\pm \rangle$). Similarly, we can analyze other situations and collate the results to derive Table 1.

Appendix B: Detailed calculation of the secure key rate and QBER

According to the definition of $q_{ij}^{\left| \alpha \right\rangle \otimes \left| \beta \right\rangle }\left( \mu _A\otimes \nu _B\right)$ in the text, the full expression of the gain and the bit error rate in Z basis are:

$$\begin{aligned}{} & {} \begin{aligned}&Q_{\mu _{A}\nu _{B}}^{Z}=\frac{1}{16} {\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{{\vert 0\rangle } \otimes {\vert 0\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert 0\rangle } \otimes {\vert 1\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) +}\\ \cdots \\ { + q_{ij}^{{\vert 3\rangle } \otimes {\vert 2\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert 3\rangle } \otimes {\vert 3\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}}\\&\quad = \frac{1}{16}{\sum _{SUCC(i,j)} \begin{bmatrix} {q_{ij}^{{\vert H\rangle }{\vert l\rangle } \otimes {\vert H\rangle }{\vert l\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert H\rangle }{\vert l\rangle } \otimes {\vert H\rangle }{\vert {- l}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) +}\\ \cdots \\ {+ q_{ij}^{{\vert V\rangle }{\vert {- l}\rangle } \otimes {\vert V\rangle }{\vert l\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert V\rangle }{\vert {- l}\rangle } \otimes {\vert V\rangle }{\vert {- l}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \end{aligned} \end{aligned}$$

(B4)

$$\begin{aligned}{} & {} \begin{aligned}&E_{\mu _{A}\nu _{B}}^{Z} =\frac{1}{Q_{\mu _{A}\nu _{B}}^{Z}} \times \frac{1}{16}{\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{{\vert 0\rangle } \otimes {\vert 0\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert 1\rangle } \otimes {\vert 1\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ {q_{ij}^{{\vert 2\rangle } \otimes {\vert 2\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert 3\rangle } \otimes {\vert 3\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \\&\quad =\frac{1}{Q_{\mu _{A}\nu _{B}}^{Z}} \times \frac{1}{16} {\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{{\vert H\rangle }{\vert l\rangle } \otimes {\vert H\rangle }{\vert l\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert H\rangle }{\vert {- l}\rangle } \otimes {\vert H\rangle }{\vert {- l}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ {q_{ij}^{{\vert V\rangle }{\vert l\rangle } \otimes {\vert V\rangle }{\vert l\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert V\rangle }{\vert {- l}\rangle } \otimes {\vert V\rangle }{\vert {- l}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \end{aligned} \end{aligned}$$

(B5)

Similarly, we can deduce $Q_{\mu _{A}\nu _{B}}^{X}$ and $E_{\mu _{A}\nu _{B}}^{X}$ in X basis:

$$\begin{aligned}{} & {} \begin{aligned}&Q_{\mu _{A}\nu _{B}}^{X} = \frac{1}{16}{\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{{\vert \varphi _{0}\rangle } \otimes {\vert \varphi _{0}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert \varphi _{0}\rangle } \otimes {\vert \varphi _{1}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) +}\\ \cdots \\ { +q_{ij}^{{\vert \varphi _{3}\rangle } \otimes {\vert \varphi _{2}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) + q_{ij}^{{\vert \varphi _{3}\rangle } \otimes {\vert \varphi _{3}\rangle }}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \\&\quad =\frac{1}{16}{\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{\frac{1}{2}{({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) +}\\ {q_{ij}^{\frac{1}{2}{({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert - \rangle }{\vert l\rangle } + {\vert + \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) + } \\ {\cdots }\\ {+ q_{ij}^{\frac{1}{2}{({{\vert + \rangle }{\vert l\rangle } - {\vert - \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) }\\ {+q_{ij}^{\frac{1}{2}{({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \end{aligned} \end{aligned}$$

(B6)

$$\begin{aligned}{} & {} \begin{aligned}&E_{\mu _{A}\nu _{B}}^{X} =\frac{1}{Q_{\mu _{A}\nu _{B}}^{X}} \times \frac{1}{16}{\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{\frac{1}{2}{({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) +} \\ \cdots \\ {+ q_{ij}^{\frac{1}{2}{({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \\&\quad =\frac{1}{Q_{\mu _{A}\nu _{B}}^{X}} \times \frac{1}{16}{\sum _{SUCC(i,j)}\begin{bmatrix} {q_{ij}^{\frac{1}{2}{({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert + \rangle }{\vert l\rangle } + {\vert - \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) +} \\ \cdots \\ {+ q_{ij}^{\frac{1}{2}{({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})} \otimes {({{\vert - \rangle }{\vert l\rangle } - {\vert + \rangle }{\vert {- l}\rangle }})}}\left( {\mu _{A} \otimes \nu _{B}} \right) } \\ \end{bmatrix}} \end{aligned} \end{aligned}$$

(B7)

In a polarization-only QKD, the actual probability of error resulting from the basis dependence defect will be:

$$\begin{aligned} E_{\mu _A\otimes \nu _B}^\omega =E_{\mu _A\otimes \nu _B}^\omega +E_d\left( 1-2E_{\mu _A\otimes \nu _B}^\omega \right) \end{aligned}$$

(B8)

where $\omega$ means one of Z or X basis, $E_d$ is the influence factor of the basis-dependent defect (calibration factor), it affects the key rate and communication distance. The measurement results are not influenced in case of reference system rotation when OAM state coding is used. In this case, $E_d=0$ which makes the error probability lower than conventional MDI-QKD protocol under the same conditions and the key rate is improved correspondingly.

In the case of decoy state, we deform Eq. 7,

$$\begin{aligned} \begin{aligned} e^{\mu _i+\nu _j}Q_{\mu _i\nu _j}^\omega&=\sum _{n,m=0}^{\infty }\frac{\mu _i^n\nu _j^m}{n!m!}Y_{nm}^\omega \\&=\sum _{m=0}^{\infty }\frac{\nu _j^m}{m!}Y_{0m}^\omega +\mu _i\left( Y_{10}^\omega {+\nu _jY}_{11}^\omega +\sum _{m=2}^{\infty }\frac{\nu _j^m}{m!}Y_{1m}^\omega \right) \\&\quad +\sum _{m=2}^{\infty }\frac{\mu _i^n}{n!}\left( Y_{n0}^\omega {+\nu _jY}_{n1}^\omega +\sum _{m=2}^{\infty }\frac{\nu _j^m}{m!}Y_{nm}^\omega \right) \\&=e^{\nu _j}Q_{0\nu _j}^\omega +e^{\mu _i}Q_{\mu _i0}^\omega -Q_{00}^\omega +\mu _i\nu _jY_{11}^\omega +h\left( \mu _i,\nu _j\right) \end{aligned} \end{aligned}$$

(B9)

where

$$\begin{aligned} h\left( \mu _i,\nu _j\right) =\sum _{m=2}^{\infty }\frac{{\mu _i\nu }_j^m}{m!}Y_{1m}^\omega +\sum _{n=2}^{\infty }\frac{\mu _i^n\nu _j}{n!}Y_{n1}^\omega +\sum _{n,m=2}^{\infty }\frac{\mu _i^n\nu _j^m}{n!m!}Y_{nm}^\omega \end{aligned}$$

(B10)

Replacing $\mu _i+\nu _j$ in Eq. B9 with the average photon number $\mu _1$ and $\nu _1$ of the signal state yields:

$$\begin{aligned}&e^{\mu _1+\nu _1}Q_{\mu _1\nu _1}^\omega -e^{\mu _2+\nu _2}Q_{\mu _2\nu _2}^\omega \nonumber \\&\quad =g_1+\left( \mu _1\nu _1-\mu _2\nu _2\right) Y_{11}^\omega +\sum _{m=2}^{\infty }\frac{{\mu _1\nu }_1^m-{\mu _2\nu }_2^m}{m!}Y_{1m}^\omega \nonumber \\&\qquad +\sum _{n=2}^{\infty }\frac{\mu _1^n\nu _1-\mu _2^n\nu _2}{n!}Y_{n1}^\omega +\sum _{n,m=2}^{\infty }\frac{\mu _1^n\nu _1^m-\mu _2^n\nu _2^m}{n!m!}Y_{nm}^\omega \nonumber \\&\quad \ge g_1+\left( \mu _1\nu _1-\mu _2\nu _2\right) Y_{11}^\omega +a\sum _{m=2}^{\infty }\frac{{\mu _1\nu }_1^m-{\mu _2\nu }_2^m}{m!}Y_{1m}^\omega \nonumber \\&\qquad +b\sum _{n=2}^{\infty }\frac{\mu _1^n\nu _1-\mu _2^n\nu _2}{n!}Y_{n1}^\omega +c\sum _{n,m=2}^{\infty }\frac{\mu _1^n\nu _1^m-\mu _2^n\nu _2^m}{n!m!}Y_{nm}^\omega \nonumber \\&\quad \ge g_1+\left( \mu _1\nu _1-\mu _2\nu _2\right) Y_{11}^\omega +\beta \left[ h\left( \mu _1,\nu _2\right) +h\left( \mu _2,\nu _1\right) \right] \nonumber \\&\quad =g_1+g_2+g_3-\left( \mu _2\nu _2-\mu _1\nu _1+\alpha \mu _1\nu _2+\beta \mu _2\nu _1\right) Y_{11}^\omega \end{aligned}$$

(B11)

In which $\beta =min\left( a,b,c\right)$. The characters a,b and c are bounded as follows:

$$\begin{aligned}{} & {} \frac{{\mu _1\nu }_1^m-{\mu _2\nu }_2^m}{{\mu _1\nu }_2^m+{\mu _2\nu }_1^m}\ge \frac{{\mu _1\nu }_1^2-{\mu _2\nu }_2^2}{{\mu _1\nu }_2^2+{\mu _2\nu }_1^2}=a\ge 0 \end{aligned}$$

(B12)

$$\begin{aligned}{} & {} \frac{\mu _1^n\nu _1-\mu _2^n\nu _2}{\mu _1^n\nu _2+\mu _1^n\nu _2}\ge \frac{\mu _1^2\nu _1-\mu _2^2\nu _2}{\mu _1^2\nu _2+\mu _1^2\nu _2}=b\ge 0 \end{aligned}$$

(B13)

$$\begin{aligned}{} & {} \frac{\mu _1^n\nu _1^m-\mu _2^n\nu _2^m}{\mu _1^n\nu _2^m-\mu _1^n\nu _2^m}\ge \frac{\mu _1^2\nu _1^2-\mu _2^2\nu _2^2}{\mu _1^2\nu _2^2-\mu _1^2\nu _2^2}=c\ge 0 \end{aligned}$$

(B14)

The parameters $g_1^\omega$,$g_2^\omega$,and $g_3^\omega$ are defined as:

$$\begin{aligned}{} & {} g_1^\omega =e^{\nu _1}Q_{0\nu _1}^\omega +e^{\mu _1}Q_{\mu _10}^\omega -e^{\nu _2}Q_{0\nu _2}^\omega +e^{\mu _2}Q_{\mu _20}^\omega \end{aligned}$$

(B15)

$$\begin{aligned}{} & {} g_2^\omega =\beta \left( e^{\mu _1+\nu _2}Q_{\mu _1\nu _2}^\omega -e^{\nu _2}Q_{0\nu _2}^\omega -e^{\mu _1}Q_{\mu _10}^\omega +Q_{00}^\omega \right) \end{aligned}$$

(B16)

$$\begin{aligned}{} & {} g_3^\omega =\beta \left( e^{\mu _2+\nu _1}Q_{\mu _2\nu _1}^\omega -e^{\nu _1}Q_{0\nu _1}^\omega -e^{\mu _2}Q_{\mu _20}^\omega +Q_{00}^\omega \right) \end{aligned}$$

(B17)

$$\begin{aligned}{} & {} Y_{11}^{\omega }\ge \frac{g_1^\omega +g_2^\omega +g_3^\omega -e^{\mu _1+\nu _1}Q_{\mu _1\nu _1}^\omega +e^{\mu _2+\nu _2}Q_{\mu _2\nu _2}^\omega }{\mu _2\nu _2-\mu _1\nu _1+\beta \mu _1\nu _2+\beta \mu _2\nu _1} \end{aligned}$$

(B18)

Similarly, deformation Eq. 8, we can obtain:

$$\begin{aligned} {e^{\mu _2+\nu _2}E}_{\mu _2\nu _2}^\omega Q_{\mu _2\nu _2}^\omega =g_4^\omega +{\mu _2\nu _2Y}_{11}^\omega e_{11}^\omega +h^\prime \left( \mu _2,\nu _2\right) \end{aligned}$$

(B19)

where,

$$\begin{aligned} g_4^\omega= & {} e^{\nu _2}Q_{0\nu _2}^\omega E_{0\nu _2}^\omega +e^{\mu _2}Q_{\mu _20}^\omega E_{\mu _20}^\omega -Q_{00}^\omega E_{00}^\omega \end{aligned}$$

(B20)

$$\begin{aligned} h^\prime \left( \mu _2,\nu _2\right)= & {} \sum _{m=2}^{\infty }\frac{{\mu _2\nu }_2^m}{m!}Y_{1m}^\omega e_{1m}^\omega +\sum _{n=2}^{\infty }\frac{\mu _2^n\nu _2}{n!}Y_{n1}^\omega e_{n1}^\omega +\sum _{n,m=2}^{\infty }\frac{\mu _i^n\nu _j^m}{n!m!}Y_{nm}^\omega e_{n1}^\omega \nonumber \\ \end{aligned}$$

(B21)

It is obvious that $h^\prime \left( \mu _2,\nu _2\right) \ge 0$, replacing $\mu _i+\nu _j$ in Eq. B19 with the average photon number $\mu _2$ and $\nu _2$ of the decoy state, we can derive:

$$\begin{aligned} e_{11}^{\omega }\le \frac{e^{\mu _2+\nu _2}Q_{\mu _2\nu _2}^\omega E_{\mu _2\nu _2}^\omega -g_4^\omega }{\mu _2\nu _2Y_{11}^\omega } \end{aligned}$$

(B22)