The author–editor game

Abstract

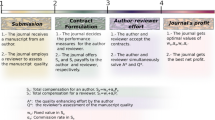
This paper provides a formal study on manuscript quality control in peer review. Within this analysis, a biased editor is defined operationally as an editor that exerts a higher (lower) level of quality control. Here we show that if the editor is more biased than the manuscript’s author then the author undertakes the type of revision that the editor prefers instead of following his or her own opinion. Moreover, authors with a strong belief about the required level of quality control will be very motivated under editors who agree with them. By contrast, when authors do not undertake the revision type that the editor prefers, they will be very demotivated under editors that exert a different level of quality control and more so as the associate editor is more biased. The effects of editors’ bias on authors’ satisfaction and motivation cause sorting in the authors who submit manuscripts to scholarly journals, and therefore, match authors and journals with similar quality standards. It will decrease the demotivating effect that editors’ bias had on some authors, so that bias becomes more effective at the peer review stage. Moreover, some journals will be forced to lower the quality standards in order to be able to compete with journals of more biased editors. This paper also shows that, under fairly weak conditions, it is optimal for the Editor-in-Chief to assign manuscripts to an editor that exerts a quality control higher than the journal’s standard, against the competing journal whose editor holds the journal’s standard.

Appendices

Appendix 1: Proof of Proposition 1

Recall that $b_E= \max (s_E, 1-s_E) \in [0.5,1]$ (respectively, $b_A= \max (s_A, 1-s_A) \in [0.5,1]$) denotes the editor’s bias (resp., the author’s bias).

At the peer review stage, the author will generate a successful revision with probability $q(e)$ by exerting effort $e$ on $[0,1]$. For simplicity, we assume that $q(e) =e$. Let $c(e)$ be the cost of such an effort $e$.

Since the actual implementation of manuscript’s revision is delegated to the author, he or she might choose to implement a $Y$-revision type (with $Y=H$ or $Y=L$) with effort level $e$ in order to maximize:

$$\begin{aligned} \max _{e; Y \in \{H, L\}} q(e) \times P(Y; Author) - c(e) \end{aligned}$$

(2)

where $P(H; Author) = s_A \gamma _A \times s_E \gamma _E$; and $P(L; Author) = (1-s_A) \gamma _A \times (1-s_E) \gamma _E$. Hence it follows that the author chooses the $Y$-type (with $Y=H$ or $Y=L$) with the highest $P(Y; Author)$:

$$\begin{aligned} Y^* = \arg \max _{Y \in \{H, L\}} P(Y; Author) \end{aligned}$$

Without loss of generality we assume that the editor chooses the $H$-type, i.e.,:

$$\begin{aligned} H = \arg \max _{Y \in \{H, L\}} P(Y; Editor) \end{aligned}$$

then it follows that $s_E > 1- s_E$ since, in this case,

$$\begin{aligned} P(H; Editor) = s_E \gamma _E > P(L; Editor ) = (1-s_E) \gamma _E. \end{aligned}$$

Hence, we have that $b_E = s_E = \max \{ s_E, 1-s_E \}$.

If the author prefers the $L$-revision type and thus $b_A = 1- s_A$, when the editor is more biased than the manuscript author $b_E > b_A$ it follows that:

$$\begin{aligned}&b_E > b_A,\end{aligned}$$

(3)

$$\begin{aligned}&\quad b_E - b_E b_A > b_A - b_E b_A,\end{aligned}$$

(4)

$$\begin{aligned}&\quad b_E (1- b_A) > (1-b_E) b_A, \end{aligned}$$

(5)

$$\begin{aligned}&\quad s_E s_A > (1-s_E)(1-s_A). \end{aligned}$$

(6)

Therefore we have that

$$\begin{aligned} P(H; Author) = s_A \gamma _A \times s_E \gamma _E > (1-s_A) \gamma _A \times (1-s_E) \gamma _E = P(L; Author) \end{aligned}$$

(7)

and the author undertakes the $H$-revision type that the editor prefers instead of following his or her own opinion (i.e., $L$-type). $\square$

Appendix 2: Proof of Proposition 2

Recall that if the editor chooses the $H$-revision type, i.e.,:

$$\begin{aligned} H = \arg \max _{Y \in \{H, L\}} P(Y; Editor) \end{aligned}$$

then it follows that $s_E > 1- s_E$ since, in this case,

$$\begin{aligned} P(H; Editor) = s_E \gamma _E > P(L; Editor ) = (1-s_E) \gamma _E \end{aligned}$$

so that $b_E = s_E = \max \{ s_E, 1-s_E \}$.

If the author chooses to follow the same revision type that the biased editor prefers, i.e., $H = \arg \max _{Y \in \{H, L\}} P(Y; Author)$, then the author chooses to implement a $H$-revision with effort level $e$ in order to maximize as follows:

$$\begin{aligned} \max _{e; Y \in \{H, L\}} q(e) \times P(Y; Author) - c(e) = \max _{e} q(e) \times P(H; Author) - c(e) \end{aligned}$$

(8)

and therefore it follows that author’s effort level $e$ solves:

$$\begin{aligned} \max _{e \in [0,1]} q(e) \times P(H; Author) - c(e) = \max _{e \in [0,1]} q(e) s_A \gamma _A s_E \gamma _E - c(e) \end{aligned}$$

(9)

where the author chooses effort $e$ to obtain the maximal payoff. Let $e(b_E)$ be the solution to this problem. Optima of unconstrained problems are found at stationary points, where the first derivative of the objective function is zero. More generally, they may be found at critical points, where the first derivative of the objective function is zero or is undefined. An equation stating that the first derivative equals zero at an interior optimum is called a “first-order condition”. Given our assumptions, the solution to our problem is defined by the first-order condition as follows:

$$\begin{aligned} e(b_E) = \frac{1}{A} s_A \gamma _A s_E \gamma _E \end{aligned}$$

(10)

since $q(e) =e$ and $c(e) = A \frac{e^2}{2}$.

Taking account that $b_E =s_E$ and using this solution for author’s effort $e(b_E)$, the relationship of effort level $e$ with respect to editor’s bias $b_E$ is as follows:

$$\begin{aligned} \frac{d \ e(b_E)}{d \ b_E} = \frac{d \ e(b_E)}{d \ s_E} = \frac{1}{A} \times s_A \gamma _A \gamma _E >0 \end{aligned}$$

(11)

This implies that optimal author’s effort $e(b_E)$ strictly increases in editor’s bias $s_E$ on an open neighbourhood of $s_E$ and $s_A$ on which the chosen revision type remains identical.

As suggested by Van den Steen (2005), by applying an envelope theorem argument on the author’s problem of maximization $\max _{e} q(e) \times s_A \gamma _A s_E \gamma _E - c(e)$ and next following completely analogous arguments as used above, we have that author’s satisfaction (i.e., author’s utility) strictly increases in editor’s bias $s_E$ on an open neighbourhood of $s_E$ and $s_A$ on which the chosen revision type remains identical. $\square$

Appendix 3: Proof of Proposition 3

If the editor chooses the $H$-revision type but the author chooses to follow the other revision type, i.e., $L = \arg \max _{Y \in \{H, L\}} P(Y; Author)$, then the author chooses to implement a $L$-revision type with effort level $e$ in order to maximize as follows:

$$\begin{aligned} \max _{e; Y \in \{H, L\}} q(e) \times P(Y; Author) - c(e) = \max _{e} q(e) \times P(L; Author) - c(e) \end{aligned}$$

(12)

and therefore it follows that author’s effort level $e$ solves:

$$\begin{aligned} \max _{e \in [0,1]} q(e) \times P(L; Author) - c(e) = \max _{e \in [0,1]} q(e) (1- s_A) \gamma _A (1- s_E) \gamma _E - c(e) \end{aligned}$$

(13)

where the author chooses effort $e$ to obtain the maximal payoff. Let $e(b_E)$ be the solution to this problem. Given our assumptions, $e(b_E)$ is defined by the first-order condition as follows:

$$\begin{aligned} e(b_E) = \frac{1}{A} (1-s_A) \gamma _A (1-s_E) \gamma _E \end{aligned}$$

(14)

since $q(e) =e$ and $c(e) = A \frac{e^2}{2}$.

Now, taking account that $b_E =s_E$ and using this solution for author’s effort $e(b_E)$, the relationship of effort level $e$ with respect to editor’s bias $b_E$ is as follows:

$$\begin{aligned} \frac{d \ e(b_E)}{d \ b_E} = \frac{d \ e(b_E)}{d \ s_E} = - \frac{1}{A} (1-s_A) \gamma _A \gamma _E < 0 \end{aligned}$$

(15)

This implies that optimal author’s effort $e(b_E)$ strictly decreases in editor’s bias $s_E$ on an open neighbourhood of $s_E$ and $s_A$ on which the chosen revision type remains identical.

Again, by applying an envelope theorem argument on the author’s problem of maximization $\max _{e} q(e) \times (1-s_A) \gamma _A (1-s_E) \gamma _E - c(e)$ and next following completely analogous arguments as used above, we have that author’s satisfaction (i.e., author’s utility) strictly decreases in editor’s bias $s_E$ on an open neighbourhood of $s_E$ and $s_A$ on which the chosen revision type remains identical. $\square$

Appendix 4: Proof of Proposition 4

Without loss of generality we assume that editor $E_1$ for journal $J_1$ prefers the $H$-revision type, i.e., $b_{E_1} = s_{E_1} = \max \{s_{E_1}, (1 - s_{E_1}) \}$.

By assumptions it follows that

$$\begin{aligned}&s_{E_1} > s_{E_2}, \end{aligned}$$

(16)

$$\begin{aligned}&\quad 1- s_{E_2} > 1- s_{E_1}, \end{aligned}$$

(17)

$$\begin{aligned}&\quad (1-s_A) (1- s_{E_2}) > (1-s_A) (1- s_{E_1}). \end{aligned}$$

(18)

Any author who submits manuscripts to journal $J_1$ but chooses the other revision type (i.e., $L$-type) gets a payoff of

$$\begin{aligned} q(e) \gamma _A \gamma _E (1-s_A) (1- s_{E_1}) - c(e) \end{aligned}$$

But this author would be strictly better off submitting to journal $J_2$ and choosing $L$-revision type:

$$\begin{aligned} q(e) \gamma _A \gamma _E (1-s_A) (1- s_{E_2}) - c(e) \end{aligned}$$

since $(1-s_A) (1- s_{E_2}) > (1-s_A) (1- s_{E_1})$ as given above. Hence, it follows that any author who submits to $J_1$ undertakes the $H$-revision type that the editor prefers. Similarly, all authors who submit to journal $J_2$ will choose the $L$-revision type.

Next, following Van den Steen (2005), given that $J_1$ (respectively $J_2$) authors choose $H$-revision (resp., $L$-revision), an author strictly prefers journal $J_1$ if:

$$\begin{aligned} \max _{e \in [0,1]} q(e) \gamma _A \gamma _E s_A s_{E_1} - c(e) > \max _{e \in [0,1]} q(e) \gamma _A \gamma _E (1-s_A) (1- s_{E_2}) - c(e). \end{aligned}$$

The point is that any author with

$$\begin{aligned} s_A > \frac{1-s_{E_2}}{s_{E_1} + (1- s_{E_2})} \end{aligned}$$

satisfies that

$$\begin{aligned}&s_A (s_{E_1} + (1- s_{E_2})) > 1-s_{E_2}, \end{aligned}$$

(19)

$$\begin{aligned}&\quad s_A s_{E_1} + s_A (1 - s_{E_2}) > 1-s_{E_2}, \end{aligned}$$

(20)

$$\begin{aligned}&\quad s_A s_{E_1} > (1-s_{E_2})- s_A(1 - s_{E_2}) = (1- s_A) (1 - s_{E_2}). \end{aligned}$$

(21)

From this equation, the desired result is demonstrated since by applying an envelope theorem argument we have that

$$\begin{aligned} s_A s_{E_1} > (1-s_A) (1- s_{E_2}) \end{aligned}$$

is equivalent to

$$\begin{aligned} \max _{e \in [0,1]} q(e) \gamma _A \gamma _E s_A s_{E_1} - c(e) > \max _{e \in [0,1]} q(e) \gamma _A \gamma _E (1-s_A) (1- s_{E_2}) - c(e) \end{aligned}$$

and therefore, we have that any author with $s_A > \frac{1-s_{E_2}}{s_{E_1} + (1- s_{E_2})}$ strictly prefers journal $J_1$, and consequently, he/she undertakes the $H$-revision type that the editor prefers.

A similar analysis proves that any author with $s_A < \frac{1-s_{E_2}}{s_{E_1} + (1- s_{E_2})}$ will submit his/her manuscript to the second journal $J_2$ and will choose the other revision type even though this type of revision might not be preferred by editor $E_2$. $\square$

Appendix 5: Proof of Proposition 5

Recall that $s_A$ measures the belief of the author that the optimal level of quality control is $Y= H$, with $H$ denoting high quality control; where authors’ beliefs about the correct course of action in order to perform manuscript’s revision are independent draws from a distribution of levels of quality control $F$ on $[0,1]$, with continuous density $f$. Now, let $F$ be a distribution that is generated from some symmetric distribution $G$ by moving some probability mass of $G$ up to obtain $F$.

From Lemma 3 in Van den Steen (2005) we can prove that, for any symmetric distribution of levels of quality control $G$, it is optimal for the Editor-in-Chief of the focal journal to assign manuscripts to a biased editor that prefers a quality control higher than the journal’s standard ($s_E >p$), against the competing journal whose non-biased editor holds the journal’s standard ($s_E=p$).

Next, by Lemma 5 in Van den Steen (2005), it then follows that if it is optimal to assign manuscripts to an biased editor with ($s_E >p$) for some symmetric distribution of levels of quality control $G$, then it is also optimal for any $F$ such that is generated from some symmetric distribution $G$ by moving some probability mass of $G$ up to obtain $F$ (e.g., a beta distribution). $\square$

Appendix 6: Examples of the author–editor game with different values of $s_E$ and $s_A$

From Figs. 6, 7, 8 and 9 that illustrate expected payoffs for the author–editor game with different values of $s_E$ and $s_A$ we obtain as follows:

• For the expected payoffs of the author–editor game with $s_E=0.75$ and $s_A=0.6$ in Fig. 6: The Nash equilibrium occurs when the Editor chooses High QC and the Author chooses High QC. Recall that the Nash equilibrium occurs when none of the agents (in our setting, the author and the editor) can unilaterally move to a better rewarding state (Osborne 2003).

• For the expected payoffs of the author–editor game with $s_E=0.6$ and $s_A=0.75$ in Fig. 7: The Nash equilibrium occurs when the Editor chooses High QC and the Author chooses High QC.

• For the expected payoffs of the author–editor game with $s_E=0.75$ and $s_A=0.2$ in Fig. 8: The Nash equilibrium occurs when the Editor chooses High QC and the Author chooses Low QC.

• For the expected payoffs of the author–editor game with $s_E=0.2$ and $s_A=0.75$ in Fig. 9: The Nash equilibrium occurs when the Editor chooses Low QC and the Author chooses Low QC.

Fig. 6

Expected payoffs for the author–editor game with $s_E=0.75$ and $s_A=0.6$

Fig. 7

Expected payoffs for the author–editor game with $s_E=0.6$ and $s_A=0.75$

Fig. 8

Expected payoffs for the author–editor game with $s_E=0.75$ and $s_A=0.2$

Fig. 9

Expected payoffs for the author–editor game with $s_E=0.2$ and $s_A=0.75$