Statistical inference for a single-index varying-coefficient model

Abstract

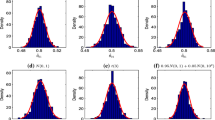
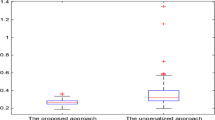
We investigate the estimators of parameters of interest for a single-index varying-coefficient model. To estimate the unknown parameter efficiently, we first estimate the nonparametric component using local linear smoothing, then construct an estimator of parametric component by using estimating equations. Our estimator for the parametric component is asymptotically efficient, and the estimator of nonparametric component has asymptotic normality and optimal uniform convergence rate. Our results provide ways to construct confidence regions for the involved unknown parameters. The finite-sample behavior of the new estimators is evaluated through simulation studies, and applications to two real data are illustrated.

Appendix

The following Lemma 1 is similar to Lemma 2 of Xia and Li (1999).

Lemma 1

Suppose that φ(u) is a bounded function and has bounded derivatives on the closed interval [a,b], and that {(U _i ,ξ _i )} is a strictly stationary and strongly mixing sequence with mixing coefficient α(n)=O(ρ ⁿ) for some 0<ρ<1. E|U _i |^r<∞, E|ξ _i |^r<∞ for all r>1, and the conditional densities $f_{U_{1},U_{l}|\xi_{1},\xi_{l}}(u_{1},u_{l}|v_{1},v_{l})$ and $f_{U_{1}|\xi_{1}}(u|v)$ are bounded for all l>1. If (C5) hold, then

where ψ _i (u)=K _h (U _i −u)φ(U _i )ξ _i .

Proof of Theorem 1

By (2.6) and Lemma 1, and similar to the proof of Theorem 2 in Wang and Xue (2011), we can prove Theorem 1, and hence omit its proof. □

Let $\mathcal{B}_{n}^{(r)}=\{\beta^{(r)}: \|\beta^{(r)}-\beta_{0}^{(r)}\|\leq c_{2}n^{-1/2}\}$ for some positive constant c ₂. Denote $\mathcal{G}=\{{\mathrm{g}}: \mathcal{U}_{w}\times\mathcal{B}\mapsto R^{q}\}$ and $\|{\mathrm{g}}\|_{\mathcal{G}}=\sup_{u\in\mathcal{U}_{w},\beta^{(r)}\in \mathcal{B}_{n}^{(r)}}\|{\mathrm{g}}(u;\beta(\beta^{(r)})\|$. Since ∥β−β ₀∥≤c ₁ n ^−1/2 and $\|\beta^{(r)}-\beta_{0}^{(r)}\|\leq c_{2}n^{-1/2}$ are equivalent when ∥β∥=1, from Theorem 1 we have $\|\hat{\mathrm{g}}-{\mathrm{g}}_{0}\|_{\mathcal{G}}=o_{P}(1)$ and $\|\hat{\dot{\mathrm{g}}}-\dot{\mathrm{g}}_{0}\|_{\mathcal{G}}=o_{P}(1)$, hence we can assume that g lie in $\mathcal{G}_{\delta}$ with δ=δ _n →0 and δ>0, where

$$ \mathcal{G}_{\delta}=\bigl\{{\mathrm{g}}\in\mathcal{G}: \|{\mathrm {g}}-{\mathrm{g}}_0\|_{\mathcal{G}}\leq \delta,\|\dot{\mathrm{g}}- \dot{\mathrm{g}}_0\|_{\mathcal{G}}\leq\delta \bigr\}. $$

(A.1)

Let ${\mathrm{g}}_{0}(\beta^{T}X;\beta)=E\{{\mathrm{g}}_{0}(\beta _{0}^{T}X)|\beta^{T}X\}$, $\dot{\mathrm{g}}_{0}(\beta^{T}X;\beta)= E\{\dot{\mathrm{g}}_{0}(\beta_{0}^{T}X)|\beta ^{T}X\}$,

and

(A.2)

It is easily known that $\mathrm{g}_{0}(\beta_{0}^{T}X;\beta_{0})=\mathrm{g}_{0} (\beta_{0}^{T}X)$, $\dot{\mathrm{g}}_{0}(\beta_{0}^{T}X;\beta_{0})=\dot{\mathrm{g}}_{0}(\beta_{0}^{T}X)$. Define the functional derivative ϖ(g₀(⋅;β),β ^(r)) of Q(ĝ,β ^(r)) with respect to g(⋅;β) at g₀(⋅;β) in the direction g(⋅;β)−g₀(⋅;β) by

We have

(A.3)

Lemma 2

Suppose that conditions (C1)–(C6) hold. Then

$$ \sup_{\beta^{(r)}\in\mathcal{B}_n^{(r)}} \bigl\|M_1\bigl(\beta^{(r)} \bigr)\bigr\| = o_P\bigl(n^{-1/2}\bigr), $$

(A.4)

$$ \sup_{\beta^{(r)}\in\mathcal{B}_n^{(r)}}\bigl\|M_2\bigl(\beta^{(r)} \bigr)\bigr\| = o_P\bigl(n^{-1/2}\bigr), $$

(A.5)

$$ \sup_{\beta^{(r)}\in\mathcal{B}_n^{(r)}} \bigl\|M_3\bigl(\beta^{(r)} \bigr)\bigr\| = o\bigl(n^{-1/2}\bigr), $$

(A.6)

$$ \sqrt{n}M_4\bigl(\beta_0^{(r)} \bigr)\stackrel{D}{\longrightarrow}N\bigl(0,\sigma^2{A}\bigr), $$

(A.7)

where A is defined in Theorem 2,

Proof

We first prove (A.4). Denote $r_{n}({\mathrm{g}},\beta^{(r)})= \sqrt{n}\{Q_{n}({\mathrm{g}},\beta ^{(r)})-Q({\mathrm{g}},\beta ^{(r)})\}$. Noting that $Q({\mathrm{g}}_{0},\beta_{0}^{(r)})=0$, we clearly have

$$ M_1\bigl(\beta^{(r)}\bigr) = n^{-1/2} \bigl\{r_n\bigl({\mathrm{g}},\beta^{(r)}\bigr)-r_n \bigl({\mathrm{g}}_0,\beta_0^{(r)}\bigr)\bigr\}. $$

(A.8)

It can be shown that the empirical process $\{r_{n}({\mathrm{g}},\beta^{(r)}):{\mathrm{g}}\in\mathcal{G}_{1},\beta ^{(r)}\in\mathcal{B}_{1}^{(r)}\}$ has the stochastic equicontinuity, where $\mathcal{B}_{1}^{(r)}=\{\beta^{(r)}: \|\beta^{(r)}-\beta^{(r)}_{0}\|\leq c_{2}\}$ and $\mathcal{G}_{1}$ are defined in (A.1) with δ=1, which are subsets of $\mathcal{B}$ and $\mathcal{G}$, respectively, and suffices for proof of (A.4) as δ<1 for n large enough by δ→0. This stochastic equicontinuity follows by checking the conditions of Theorem 1 in Doukhan et al. (1995). Therefore, we have $r_{n}({\mathrm{g}},\beta^{(r)})-r_{n}({\mathrm{g}}_{0},\beta_{0}^{(r)})=o_{P}(1)$, uniformly for ${\mathrm{g}}\in\mathcal{G}_{1}$ and $\beta^{(r)}\in\mathcal{B}_{1}^{(r)}$. This together with (A.8) proves (A.4).

We now prove (A.5). It follows from (A.3) that

Therefore, from Theorem 1 we can prove (A.5).

From condition (C2) and Theorem 1, it is easy to prove (A.6). We now prove (A.7). Let f ₀(u) denote the density function of $\beta_{0}^{T}X$. Similar to the proof of Theorem 1 in Wang and Xue (2011), we can prove

(A.9)

uniformly for $u\in\mathcal{U}_{w}$ and $\beta\in\mathcal{B}_{n}^{(r)}$, where c _n =n ^−1/2+h ² and D(u) is defined in condition (C6).

By (A.3) and using the dominated convergence theorem (Loève 2000), we can obtain

where C(⋅) and μ ₂ are defined in (C6) and Theorem 3, respectively. This together with (A.2) and the definition of $M_{4}(\beta_{0}^{(r)})$ proves that

where $\zeta_{i}=V_{i} - {C}(\beta_{0}^{T}X_{i}){D}^{-1}(\beta_{0}^{T}X_{i})Z_{i}$ and $V_{i}= J_{\beta_{0}^{(r)}}^{T}X_{i}\dot{\mathrm{g}}_{0}^{T}(\beta _{0}^{T}X_{i})Z_{i}w(\beta_{0}^{T}X_{i})$. Therefore, by the central limit theorem for dependent data (Rio 1995) and Slutsky’s theorem, we get

$$\sqrt{n}M_4(\hat{\mathrm{g}},\beta_0)= \frac{1}{\sqrt{n}} \sum_{i=1}^n\varepsilon_i \zeta_i+o_P(1) \stackrel{D}{\longrightarrow}N\bigl(0, \sigma^2{A}\bigr). $$

This proves (A.7). The proof of Lemma 2 is completed. □

Proof of Theorem 2

Using the notations of Lemma 2, we have

(A.10)

In light of $Q({\mathrm{g}}_{0},\beta_{0}^{(r)})=0$, we have by the Taylor expansion that

$$ Q\bigl({\mathrm{g}}_0,\beta^{(r)}\bigr) = -{B}\bigl(\beta^{(r)}-\beta^{(r)}_0 \bigr)+o_P\bigl(n^{-1/2}\bigr), $$

(A.11)

uniformly for $\beta^{(r)}\in\mathcal{B}_{n}^{(r)}$. By (A.10), (A.11) and (A.4)–(A.6) of Lemma 2, we have

$$Q_n\bigl(\hat{\mathrm{g}},\beta^{(r)}\bigr)=M_4 \bigl(\beta_0^{(r)}\bigr) - {B}\bigl({\beta}^{(r)}- \beta_0^{(r)}\bigr) + o_P\bigl(n^{-1/2} \bigr), $$

uniformly for ${\mathrm{g}}\in\mathcal{G}_{\delta}$ and $\beta ^{(r)}\in\mathcal{B}_{n}$. Noting that $Q_{n}(\hat{\mathrm{g}},\hat{\beta}^{(r)})=0$, from the foregoing equation we get

$$ \hat{\beta}^{(r)}-\beta^{(r)}_0 = {B}^{-1}M_4\bigl(\beta_0^{(r)}\bigr) + o_P\bigl(n^{-1/2}\bigr). $$

(A.12)

We now consider the estimator $\hat{\beta}$. By simple calculation, we have

$$ \hat{\beta}-\beta_0={J}_{\beta_0^{(r)}} \bigl(\hat{ \beta }^{(r)}-\beta_0^{(r)} \bigr)+O_P \bigl(n^{-1} \bigr). $$

(A.13)

From (A.12) and (A.13), we have

$$\sqrt{n}(\hat{\beta}-\beta_0)=\sqrt{n}\,{J}_{\beta_0^{(r)}}{B }^{-1}M_4\bigl(\beta^{(r)}_0\bigr) + o_P(1). $$

This together with (A.7) of Lemma 2 proves Theorem 2. □

Proof of Theorem 3

By (A.9) and Theorem 4.4 of Masry and Tjøstheim (1995), we can complete the proof of Theorem. □

The proof of Theorem 4 is similar to the proof of the second part of Theorem 2 in Xia and Li (1999), and hence the detail is omitted.