A pseudo-marginal sequential Monte Carlo algorithm for random effects models in Bayesian sequential design

Abstract

Motivated by the need to sequentially design experiments for the collection of data in batches or blocks, a new pseudo-marginal sequential Monte Carlo algorithm is proposed for random effects models where the likelihood is not analytic, and has to be approximated. This new algorithm is an extension of the idealised sequential Monte Carlo algorithm where we propose to unbiasedly approximate the likelihood to yield an efficient exact-approximate algorithm to perform inference and make decisions within Bayesian sequential design. We propose four approaches to unbiasedly approximate the likelihood: standard Monte Carlo integration; randomised quasi-Monte Carlo integration, Laplace importance sampling and a combination of Laplace importance sampling and randomised quasi-Monte Carlo. These four methods are compared in terms of the estimates of likelihood weights and in the selection of the optimal sequential designs in an important pharmacological study related to the treatment of critically ill patients. As the approaches considered to approximate the likelihood can be computationally expensive, we exploit parallel computational architectures to ensure designs are derived in a timely manner.

1 Introduction

Experiments for the collection of data in batches or blocks are prevalent in applied science and technology in areas such as pharmacology (Mentré et al. 1997), agriculture (Patterson and Hunter 1983) and aeronautics (Woods and van de ven 2011). When modelling data from such experiments, it is important to account for the correlation or dependence of observations collected in a given batch or a given block. The same is of course true when constructing an optimal experimental design. Unfortunately, this task is generally computationally prohibitive, and therefore has received limited attention from researchers. In a sequential design setting, the computational challenge is efficiently updating prior information as new data are observed and the need to find an optimal design for the collection of data from the next batch or block each time this prior information has been updated. The latter requires locating the design that maximises the expected utility where this expected utility is generally a functional of the posterior distribution averaged over uncertainty in the model, parameter values and supposed observed data. Hence, it is necessary to efficiently sample from or accurately approximate a larger number of posterior distributions. This poses a significant computational challenge and renders many algorithms such as standard Markov chain Monte Carlo (MCMC) computationally infeasible (Ryan et al. 2015). Hence, the requirement for an efficient computational algorithm for Bayesian inference motivates the consideration of the sequential Monte Carlo (SMC) algorithm. Computational efficiency is achieved when using the SMC algorithm as prior information can be updated as more data are observed avoiding the need to re-run posterior sampling approaches based on the full data set. Further, in using the SMC algorithm, one can handle model uncertainty by running SMC algorithms for each rival model (Drovandi et al. 2014) avoiding any between-model moves. One also avoids computationally expensive approximations of the evidence or marginal likelihood of a given model through the availability of a convenient approximation which is a by-product of the SMC algorithm (Del Moral et al. 2006).

The particular design problem considered in this work is a sequential design problem in pharmacology, and involves pharmacokinetic (PK) models and extra corporeal membrane oxygenation (ECMO). In 2009, during the worldwide H1N1 pandemic, ECMO was a vital treatment for H1N1 patients requiring advanced ventilator support in Australia and internationally (Davies et al. 2009). ECMO is a modification of cardiopulmonary bypass (CPB). However, unlike conventional CPB, ECMO is utilised in already critically ill patients, and lasts for days rather than hours increasing the likelihood of complications. Nonlinear random effect models for data from such trials have been considered recently (Ryan et al. 2014). As the likelihood based on a value of the random effects is available analytically, these models are, in principle, straightforward to estimate, for example, via MCMC. However, the need to draw from many posterior distributions renders this sampling method computationally infeasible in the context of experimental design, and thus we propose a new SMC algorithm for sequential design and inference.

To apply the SMC algorithm in the PK context (and in general), the likelihood needs to be evaluated a large number of times. Unfortunately, for nonlinear random effect models, this likelihood is typically unavailable analytically (Kuk 1999). We therefore propose to unbiasedly estimate the likelihood within SMC forming an exact-approximate algorithm to facilitate efficient Bayesian inference and design for random effects models. In our research, we consider four approaches for the approximation. Firstly, we consider standard Monte Carlo (MC) integration. Here, Q random effect values are randomly drawn from the (current) prior distribution, and the average conditional likelihood (over Q) is taken as the estimate of the likelihood. Secondly, we extend standard MC integration by choosing randomised low discrepancy sequences of random numbers for the integration. This is known as randomised quasi-Monte Carlo (RQMC), and can yield more efficient estimates when compared to standard MC (Niederreiter 1978). Thirdly, we consider Laplace importance sampling (LIS) where a Laplace approximation is used to form the importance distribution in importance sampling (Kuk 1999). Lastly, we consider the combination of LIS and RQMC where draws from the importance distribution are chosen as (transformed) randomised low discrepancy random numbers. These approaches form new pseudo-marginal algorithms for random effect models, and are explained in Sect. 3. We also compared these methods within a sequential Bayesian design context in Sect. 5.

To facilitate the construction of designs in a reasonable amount of time, we propose the exploitation of parallel computational architectures. In particular, we explore the use of a graphics processing unit (GPU). We are not aware of the use of such hardware in the derivation of optimal designs. However, they have been used recently within SMC to reduce run times (Durham and Geweke 2011; Vergé et al. 2015). Actually, the SMC algorithm is often labelled an “embarrassingly parallel” algorithm (see for example Gramacy and Polson (2011)), and hence naturally lends itself to such endeavors. We note that our use of the GPU is not within the standard SMC algorithm but rather for the approximation of the likelihood.

A recent review of modern computational algorithms for Bayesian design has been given by Ryan et al. (2015), and discusses some work in a sequential design context. Approaches based on MCMC techniques have been explored for fixed effects models by Weir et al. (2007), McGree et al. (2012). In each case, importance sampling was used in selecting the next design point to avoid running many MCMC posterior simulations. Approaches based on SMC have also been considered for fixed effects models by Drovandi et al. (2013, 2014). In the 2013 paper, a variety of utility functions were considered to construct a design to precisely estimate model parameters. In the following 2014 paper, a utility function for model discrimination was developed and applied within a number of nonlinear settings. The generic algorithms used in both of these papers provides a basis for the work proposed in this paper. However, this generic algorithm was limited to independent data settings, and therefore our proposed methods for random effect models present a significant extension of this previous research.

Müller (1999) has considered an MCMC approach to derive static (non sequential) Bayesian experimental designs by considering the design variable as random and exploring a target distribution comprised of the design variable, the model parameter and the data. Extensions to this approach have been given by Amzal et al. (2006) who used a particle method to explore the utility surface and employed simulated annealing (Corana et al. 1987) to concentrate the samples near the modes. Such methodology has been applied in Bayesian experimental design, but is currently restricted to simply comparing fixed designs (Han and Chaloner 2004), optimising designs in low dimensions, for a single, fixed effects model (Müller 1999) and/or limited utility functions (Stroud et al. 2001).

Our paper proceeds with a description of the inference framework within which we develop our methodology. This is followed by Sect. 3 which decribes our proposed SMC algorithm for random effects models. In Sect. 4, we define a utility function called Bayesian A-optimality for parameter estimation and show how it is approximated within our algorithm. In Sect. 5, our proposed methods are applied to a PK study in sheep. We conclude with a discussion of our work, and suggestions for further research.

2 Inferential framework

Consider the sequential problem where a design is required for the collection of data in a batch or block to precisely estimate parameters across one or a finite number of K models defined by the random variable $M\in \{1,\ldots ,K \}$. We follow the M-closed perspective of Bernardo and Smith (2000), and assume that one of the K models is appropriate to describe the observed data. Each model m contains parameters $\varvec{\theta }_m = (\varvec{\mu }_m,\varvec{\varOmega }_m,\sigma _m)$ defining the model parameters $\varvec{\mu }_m$, the between batch or block variability of the model parameters $\varvec{\varOmega }_m$ and the residual variability parameter $\sigma _m$. Note that the subscript m will be dropped if only one model is under consideration. Define the likelihood function $f(\varvec{y}_{1:j}|M=m, \varvec{\theta }_m, \varvec{d}_{1:j})$ for all data $\varvec{y}_{1:j}$ observed up to batch or block j at design points $\varvec{d}_{1:j}$. To construct this likelihood for each model, we assume that batch/block effects are independent random draws from a population of batches/blocks so that data from block j denoted as $y_{j}$ are conditionally independent of $\varvec{y}_{1:j-1}$ and $\varvec{d}_{1:j-1}$ given $d_j$. Then, the likelihood is formed as follows:

$$\begin{aligned}&f\left( \varvec{y}_{1:j} | M=m, \varvec{\theta }_m, \varvec{d}_{1:j}\right) \\&\quad = \varPi _{k = 1}^j f\left( y_k | M=m, \varvec{\theta }_m, d_k\right) , \quad \text{ for } \quad j = 1,\ldots ,J. \end{aligned}$$

Then, the likelihood for data from batch or block j can be expressed as

$$\begin{aligned} f\left( y_{j}|M=m,\varvec{\theta }_m, d_{j}\right)= & {} \int f\left( y_{j}|\varvec{b}_{mj},M=m,\varvec{\theta }_m,d_{j}\right) \nonumber \\&\times p\left( \varvec{b}_{mj}|\varvec{\mu }_m,\varvec{\varOmega }_m,M=m\right) d\varvec{b}_{mj}, \nonumber \\ \end{aligned}$$

(1)

where $\varvec{b}_{mj} \sim p(\varvec{\mu }_m,\varvec{\varOmega }_m| M=m)$ denotes the random effect associated with block j for model m.

Prior distributions are placed on $\varvec{\theta }_m$ for each model denoted as $p(\varvec{\theta }_m | M=m)$, and we also define a probability distribution for the random effects $p(\varvec{b}_{mj}|\varvec{\mu }_m,\varvec{\varOmega }_m, M=m)$, where in our work this is a multivariate normal distribution with mean $\varvec{\mu }_m$ and variance-covariance $\varvec{\varOmega }_m$ for model m. We also place prior model probabilities on each model denoted as $p(M=m)$. All of this prior information is sequentially updated as data are observed on each block, and then used in finding the optimal design for data collection in the next batch or block.

3 Sequential Monte Carlo algorithm

SMC is an algorithm for sampling from a smooth sequence of target distributions. Originally developed for dynamic systems and state space models (Gordon et al. 1994; Liu and Chen 1998), the algorithm has also been applied to static parameter models through the use of a sequence of artificial distributions (Chopin 2002; Del Moral et al. 2006). In our sequential design setting, the sequence of target distributions presents as a sequence of posterior distributions through data annealing (for example, see Gilks and Berzuini 2001). We first introduce the standard or idealised SMC algorithm, then present our new developments.

3.1 Idealised sequential Monte Carlo algorithm

As given in Chopin (2002), for a particular model m, the sequence of target distributions built up through data annealing is given by

$$\begin{aligned}&p\left( \varvec{\theta }_m | M=m, \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \propto f\left( \varvec{y}_{1:j}|M=m, \varvec{\theta }_m, \varvec{d}_{1:j}\right) \\&\quad \times p\left( \varvec{\theta }_m|M=m\right) , \quad \text{ for } \quad j = 1,\ldots ,J. \end{aligned}$$

For a given model, there are essentially three steps in the SMC algorithm; re-weighting, resampling and mutation steps. As data are observed, the algorithm generates a set of N weighted particles for each model m to represent each target/posterior distribution in the sequence. This is achieved by initially drawing equally weighted particles for each model from the respective prior distributions. As data are observed, particles for each model are continually re-weighted via importance sampling (Hammersley and Handscomb 1964) until the effective sample size ($ESS_m$) of the importance approximation of the current target distribution for each model falls below a predefined threshold (E). For models where $ESS_m < E$, within model resampling is performed to replicate particles with relatively large weight while eliminating particles with relatively small weight. This is followed by the mutation step where an MCMC kernel (Metropolis et al. 1953; Hastings 1970) that maintains invariance of the current target is used to diversify each particle set. Alternative kernels are possible that lead to ${\mathcal {O}}(N^2)$ rather than ${\mathcal {O}}(N)$ SMC algorithms (Del Moral et al. 2006).

In using this SMC algorithm, there is also the availability of an efficient estimate of the evidence for a given model (leading to an efficient estimate of posterior model probabilities). As shown in Del Moral et al. (2006), the evidence of a given model can be approximated as a by-product of the SMC algorithm. To show this, we note that the ratio of normalising constants for a given model m $(Z_{m,j+1}/Z_{m,j})$ is equivalent to the predictive distribution of the next observation $y_{j+1}$ given current data $\varvec{y}_{1:j}$:

$$\begin{aligned} Z_{m,j+1}/Z_{m,j}= & {} \int _{\varvec{\theta }_m} f\left( y_{j+1} | M=m,\varvec{\theta }_m, d_{j+1}\right) \\&\times p\left( \varvec{\theta }_m |M=m, \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) d\varvec{\theta }_m. \end{aligned}$$

Here, we form a particle approximation to the above integral as follows:

$$\begin{aligned} Z_{m,j+1}/Z_{m,j} \approx \sum _{i = 1}^N W_{m,j}^i f\left( y_{j+1} | M=m,\varvec{\theta }_{m,j}^{i}, d_{j+1}\right) . \end{aligned}$$

This approximation of the evidence is therefore available at negligible additional computational cost, and allows for efficient design and analysis in sequential settings where there exists uncertainty about the model (Drovandi et al. 2014).

3.2 Pseudo-marginal sequential Monte Carlo algorithm for random effect models

Implementing the idealised SMC algorithm requires evaluating the likelihood many times (in the re-weight and move steps). Unfortunately for nonlinear random effect models, this is generally analytically intractable, see Eq. (1). Here, we propose to extend the idealised SMC algorithm to random effect models through unbiasedly approximating this likelihood. Four different approaches are considered for this approximation. Firstly, we consider standard MC integration for the approximation. For each particle of a given model $\varvec{\theta }_m^{i}$, the likelihood can be approximated as follows:

$$\begin{aligned} f\left( y_{j}|M=m,\varvec{\theta }_m^{i},d_{j}\right)= & {} \int f\left( y_{j}|\varvec{b}_{mj},M=m,\varvec{\theta }_m^{i},d_{j}\right) \nonumber \\&\times p\left( \varvec{b}_{mj}|\varvec{\mu }^{i}_m,\varvec{\varOmega }^{i}_m, M=m\right) d\varvec{b}_{mj},\nonumber \\\approx & {} \frac{1}{Q}\sum _{q=1}^Q f\left( y_{j}|\varvec{b}_{mj}^q,M=m,\varvec{\theta }^{i}_m,d_{j}\right) \nonumber \\= & {} \hat{f}\left( y_{j}|M=m,\varvec{\theta }_m^{i},d_{j}\right) , \end{aligned}$$

(2)

where

$$\begin{aligned} \varvec{b}_{mj}^q\mathop {\sim }\limits ^{iid} p\left( .|\varvec{\mu }_m^{i},\varvec{\varOmega }_m^{i},M=m\right) ,\;\;q=1,\ldots ,Q. \end{aligned}$$

Alternatively, QMC methods can be used to approximate the integral in Eq. (2). To implement QMC, the Q integration nodes are replaced with (transformed) deterministic nodes that are more evenly distributed over $(0,1]^{dim(\varvec{\mu }_m)}$. Examples of such sequences include the Halton (Halton 1960), Sobol’ (Sobol’ 1967) and Faure (Faure 1982) sequences. In order to maintain an unbiased estimate, randomised versions of these deterministic sequences can be used. Here, we consider a rank-1 lattice shift which entails applying a random shift modulo 1 (Cranley and Patterson 1976; L’Ecuyer and Lemieux 2000) and the Baker’s transformation to each coordinate in the sequence. Pseudo code for this is given in Algorithm 1, where $v_k$ is the shift applied to the lattice. Such an approach has been used to estimate the likelihood function of a mixed logit model (Munger et al. 2012).

Implementing this approach to randomise the deterministic sequences in our framework means that the actual values of $\varvec{b}_{mj}^q$ are based on $\varvec{u}_q \in (0,1]^{dim(\varvec{\mu }_m)}$ that are more evenly distributed over $(0,1]^{dim(\varvec{\mu }_m)}$ than random draws. Such an approach is termed RQMC, and has been shown to be superior to standard Monte carlo integration in terms of the efficiency of an estimate (Morokoff and Caflisch 1995). In our work, the random shift is applied to an initial Halton sequence of length Q in $(0,1]^{dim(\varvec{\mu }_m)}$ each ‘new’ time the likelihood is estimated. This ensures appropriate unbiasedness for our exact-approximate algorithm. Then, the Cholesky factorization of $\varvec{\varOmega }_m^{i}$ is found and applied to the $\varPhi ^{-1} (\varvec{u}_q)$s to generate the $\varvec{b}_{mj}^q$s from the appropriate distribution, where $\varPhi$ denotes the normal cumulative distribution function.

The third approach we consider to approximate this likelihood is LIS. This approach was proposed by Kuk (1999) to estimate the likelihood for generalised linear mixed models. For each particle $\varvec{\theta }_m^{i}$, a numerical optimiser was used to find the mode of the following with respect to $\varvec{b}_{mj}$:

$$\begin{aligned} f\left( y_{j}|\varvec{b}_{mj},M=m,\varvec{\theta }_m^{i},d_{j} \right) p\left( \varvec{b}_{mj}|\varvec{\mu }^{i},\varvec{\varOmega }^{i}_m,M=m\right) , \end{aligned}$$

and a multivariate Normal distribution (denoted as $p_{LA}(\varvec{\mu }^i_{LA}, \varvec{\varOmega }^i_m, M=m)$) was formed with mean $\varvec{\mu }^i_{LA}$ being the mode and the variance-covariance matrix $\varvec{\varOmega }^i_m$ being the random effect variability corresponding to the ith particle for model m. Then, by noting that

$$\begin{aligned}&f\left( y_{j}|M=m,\varvec{\theta }_m^{i},d_{j}\right) \nonumber \\&\quad = \int \frac{f\left( y_{j}|\varvec{b}_{mj},M=m, \varvec{\theta }_m^{i},d_{j}\right) p \left( \varvec{b}_{mj}|\varvec{\mu }^{i}_{m},\varvec{\varOmega }^{i}_m,M=m \right) }{p_{LA}\left( \varvec{b}_{mj}|\varvec{\mu }^i_{LA}, \varvec{\varOmega }^i_m,M=m\right) } \nonumber \\&\quad \quad \times p_{LA}\left( \varvec{b}_{mj}|\varvec{\mu }^i_{LA}, \varvec{\varOmega }^i_m, M=m\right) d\varvec{b}_{mj}, \end{aligned}$$

(3)

the likelihood can be approximated as follows:

$$\begin{aligned}&\hat{f}\left( y_{j}|M=m,\varvec{\theta }_m^{i},d_{j}\right) \\&\quad = \frac{1}{Q}\sum _{q=1}^Q \frac{f\left( y_{j}|\varvec{b}_{mj}^q,M=m,\varvec{\theta }_m^{i},d_{j} \right) p\left( \varvec{b}_{mj}^q|\varvec{\mu }^{i}_m,\varvec{\varOmega }^{i}_m,M=m \right) }{p_{LA}\left( \varvec{b}_{mj}^q|\varvec{\mu }^i_{LA}, \varvec{\varOmega }^i_m,M=m\right) }, \end{aligned}$$

where $\varvec{b}_{mj}^q \sim p_{LA}(\varvec{\mu }^i_{LA}, \varvec{\varOmega }^i_m,M=m)$ for each particle i.

The fourth approach combines LIS and RQMC. Instead of drawing randomly from the Laplace approximation, these draws are chosen based on randomised Halton sequences using $\varvec{\mu }^i_{LA}$ and $\varvec{\varOmega }^i_m$.

In comparing these approximations, standard MC and RQMC will potentially perform poorly when the corresponding Laplace approximation does not overlap with the prior density $p(\varvec{b}_{mj} | \varvec{\mu }_m^i,\varvec{\varOmega }_m^{i},M=m)$, with MC generally producing more variable weights. Such cases could occur, for example, when the random effect values are relatively far from $\varvec{\mu }_m^i$. Hence, it is believed that MC and RQMC will produce more variable likelihood weights (and therefore more variable estimates) than LIS and LIS+RQMC. However, this comes at the computational cost of finding the mode for each particle. This potential trade-off between variability of weights and computational cost will be explored in Sect. 5.

Any of the above approaches can be used to unbiasedly approximate the likelihood to form a pseudo-marginal SMC algorithm for random effect models. Andrieu and Roberts (2009) consider a similar psuedo-marginal approach within an MCMC framework, and Tran et al. (2014) consider Bayesian inference via importance sampling for models with latent variables based on an unbiased estimate of the likelihood. Our algorithm is similar to the framework proposed by Chopin et al. (2013) for state space models. Further, there have been developments using QMC and RQMC in the SMC algorithm, see Gerber and Chopin (2014) who provide empirical evidence that using QMC methods may significantly outperform the standard implementation of SMC in terms of approximation error. As noted in Gerber and Chopin (2014), the error rate for standard MC is ${\mathcal {O}}(N^{-1/2})$ improving to ${\mathcal {O}}(N^{-1+\epsilon })$ using QMC, and improving again to ${\mathcal {O}}(N^{-3/2+\epsilon })$ using RQMC, under certain conditions (Owen 1997a, b, 1998b). Owen (1998a) also proposed a method based on RQMC for ‘very high’ dimensional problems, but notes that the advantages of using QMC and RQMC diminish as the dimension increases or for integrals that are not smooth (Morokoff and Caflisch 1995).

3.3 Implementation of the pseudo-marginal sequential Monte Carlo algorithm

Pseudo code for our SMC algorithm is given in Algorithm 2, and now explained. Let $\{ W_{m,j}^i, \varvec{\theta }_{m,j}^i \}_{i=1}^N$ denote the particle approximation for model m, for target $p_j(.)$, then the re-weight step is given by

$$\begin{aligned} w_{m,j+1}^i = W_{m,j}^i \hat{f}\left( y_{j+1} | M=m, \varvec{\theta }_{m,j}^{i}, d_{j+1}\right) , \end{aligned}$$

as the batch or block data are conditionally independent and an MCMC kernel is used in the mutation step. From Chopin (2002) and Del Moral et al. (2006), the $\hat{f}(y_{j+1} | M=m, \varvec{\theta }_{m,j}^{i}, d_{j+1})$ are the approximate incremental weights given by target $j+1$ divided by target j, and are given by the approximate likelihood, Eq. (2). Once the new weights $w_{m,j+1}^i$ are normalized to give $W_{m,j+1}^i$, the particle approximation $\{ W_{m,j+1}^i, \varvec{\theta }_{m,j}^i \}_{i=1}^N$ approximates target $j+1$.

We assess the adequacy of this approximation by estimating the $ESS_m$ by $1/\sum _{i=1}^N (W_{m,j+1}^i)^2$ (Liu and Chen 1995). If the $ESS_m$ falls below E, the particle set is replenished by resampling the particles with probabilities proportional to the normalised weights. In our work, we used multinomial resampling. However, other resampling techniques such as systematic or residual resampling could be considered (Kitagawa 1996). Following this step, the particles are diversified by applying $R_m$ MCMC steps to each particle to increase the probability of the particle moving. Assuming a symmetric proposal distribution, the acceptance probability $\alpha$ for a proposal $\varvec{\theta }^{*}_{m,j+1}$ for a given model is given by the Metropolis probability

$$\begin{aligned} \alpha = \min \left\{ \frac{p\left( \varvec{\theta }^*_{m, j+1}\right) \hat{f}\left( \varvec{y}_{1:j+1} | M=m, \varvec{\theta }_{m,j+1}^{*}, \varvec{d}_{1:j+1}\right) }{p\left( \varvec{\theta }^i_{m, j+1}\right) \hat{f}\left( \varvec{y}_{1:j+1} | M=m, \varvec{\theta }_{m,j+1}^i, \varvec{d}_{1:j+1}\right) } , 1 \right\} . \end{aligned}$$

The proposal distribution in the MCMC kernel q(.|.) is efficiently constructed based the current set of particles (as they are already distributed according to the target $p_{j+1}(.)$). This avoids tuning the algorithm or having to implement other schemes such as adaptive MCMC. We also note that as each rival model has a particle set, any between model ‘jumps’ are avoided.

As shown in Sect. 3.1, there is also the availability of an efficient estimate of the evidence for a given model. For random effect models, we base this on the approximate likelihood. We note that an estimate of the evidence is generally difficult to obtain for nonlinear models, and, in particular, mixed effects models. The particle approximation for Eq. (3) is then based on the approximate likelihood as follows:

$$\begin{aligned} Z_{m,j+1}/Z_{m,j} \approx \sum _{i = 1}^N W_{m,j}^i \hat{f}\left( y_{j+1} | M=m,\varvec{\theta }_{m,j}^{i}, d_{j+1}\right) . \end{aligned}$$

Tran et al. (2014) show the validity of this estimate. As $Z_0 = 1$, the evidence can be approximated sequentially in the algorithm as data are observed. Further, posterior model probabilities $p(m|\varvec{y}_{1:j+1}, \varvec{d}_{1:j+1})$ are estimated based on the above estimates of evidence (for each given model).

4 Experimental design

SMC has been employed within a sequential design framework for estimation of a fixed effects model (Drovandi et al. 2013) and for discriminating between fixed effects models (Drovandi et al. 2014). In each paper, appropriate utility functions were defined for the experimental goals. Here, we consider an estimation utility termed Bayesian A-optimality, and extend to the case where one wishes to precisely estimate parameters over a finite number of models. This utility is based on A-optimality (Kiefer 1959), where the total or average variance of the parameter estimates is minimised (Atkinson et al. 2007).

Consider a design $\varvec{d}$. In general, the expected utility for this design for a single model can be expressed as

$$\begin{aligned} u(\varvec{d}) = \int _{\varvec{\theta }} \int _{\varvec{y}} u(\varvec{d},\varvec{\theta },\varvec{y})p(\varvec{\theta }, \varvec{y} | \varvec{d}) \text{ d }\varvec{y} \text{ d }\varvec{\theta }. \end{aligned}$$

(4)

This can be extended as follows when uncertainty about the true model is considered

$$\begin{aligned} u\left( \varvec{d}\right)= & {} \sum _{m = 1}^K p\left( M=m|\varvec{y},\varvec{d}\right) \int _{\varvec{\theta }_m} \int _{\varvec{y}} u\left( \varvec{d},\varvec{y},m,\varvec{\theta }\right) \nonumber \\&\times \,p\left( \varvec{\theta }_m, \varvec{y}, M=m| \varvec{d}\right) \text{ d }\varvec{y} \text{ d }\varvec{\theta }_m. \end{aligned}$$

(5)

Two utility functions will be considered in the examples that follow. For a single model, the utility is given by the inverse of the trace of the posterior variance; Bayesian A-optimality as follows:

$$\begin{aligned} u(\varvec{d},\varvec{y}) = 1/\text{ trace }~\left( \text{ VAR }\left[ \varvec{\theta } |\varvec{y}, \varvec{d}\right] \right) . \end{aligned}$$

This is extended to the case of K models by maximising the inverse of the product of the Bayesian A-optimality utility values over the K models (scaled appropriately such that each utility value is between 0 and 1). This can be simplified by taking the logarithm which leads to the consideration of maximising the inverse of the sum of the logarithm of traces of the posterior variances for all K models. That is,

$$\begin{aligned} u(\varvec{d},\varvec{y}) = 1/\sum _{l=1}^{K}\log \text{ trace }~\left( \text{ VAR }[\varvec{\theta }_l |\varvec{y}, \varvec{d}, M=l]\right) . \end{aligned}$$

We now show how to estimate utilities of the forms given in Eqs. (4) and (5) in a sequential design framework. Suppose we have collected data up until batch or block j denoted as $\varvec{y}_{1:j}$ collected at design points $\varvec{d}_{1:j}$. Define a general utility $u({\varvec{d}},z,m,\varvec{\theta }_m | \varvec{y}_{1:j},\varvec{d}_{1:j})$, where $\varvec{d}$ is a proposed design for future observation z taken from model m with parameter $\varvec{\theta }_m$. Then, the expected utility of a given design $\varvec{d}$ conditional on data already observed $\varvec{y}_{1:j}$ at design points $\varvec{d}_{1:j}$, denoted as $u(\varvec{d} | \varvec{y}_{1:j},\varvec{d}_{1:j})$, is given by

$$\begin{aligned} u\left( \varvec{d} | \varvec{y}_{1:j},\varvec{d}_{1:j}\right)= & {} E_{z,m,\varvec{\theta }_m | \varvec{y}_{1:j}, \varvec{d}_{1:j}}\left[ u\left( \varvec{d},z,m,\varvec{\theta }_m | \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \right] \\= & {} \sum _{m = 1}^K \int _z \int _{\varvec{\theta }_m} u\left( \varvec{d},z,m,\varvec{\theta }_m | \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \\&\times p\left( z,m,\varvec{\theta }_m | \varvec{y}_{1:j}, \varvec{d}_{1:j}, \varvec{d}\right) d\varvec{\theta }_m dz \\= & {} \sum _{m = 1}^K \int _z \int _{\varvec{\theta }_m} u\left( \varvec{d},z,m,\varvec{\theta }_m | \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \\&\times p\left( z|m,\varvec{\theta }_m, \varvec{y}_{1:j}, \varvec{d}_{1:j},\varvec{d}\right) \\&\times p\left( \varvec{\theta }_m | m, \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \\&\times p\left( m | \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) d\varvec{\theta }_m dz \\= & {} \sum _{m = 1}^K p\left( m | \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \\&\int _z \int _{\varvec{\theta }_m} u\left( \varvec{d},z,m,\varvec{\theta }_m | \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \\&\times p\left( z|m,\varvec{\theta }_m,\varvec{d}\right) p\left( \varvec{\theta }_m | m, \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) d\varvec{\theta }_m dz, \end{aligned}$$

where the summation over the posterior model probabilities is dropped if only a single model is under consideration.

As shown in Algorithm 2, suppose, up to batch or block j, we have a particle set for each model defined as $\{ W_{m,j}^i, \varvec{\theta }_{m,j}^i \}_{i=1}^N$, for $m = 1,\ldots ,K$. We approximate the above integrals via simulating $z_{m,j}^i$ from the posterior predictive distribution $p(z|m,\varvec{\theta }_{m,j}^i,\varvec{d})$. This gives a weighted sample $\{ W_{m,j}^i, \varvec{\theta }_{m,j}^i, z_{m,j}^i \}$ from $p(z,\varvec{\theta }_m | m, \varvec{y}_{1:j}, \varvec{d}_{1:j}, \varvec{d})$. Then, MC integration can be used to approximate the above integrals as follows:

$$\begin{aligned} u\left( \varvec{d} | \varvec{y}_{1:j},\varvec{d}_{1:j}\right)\approx & {} \sum _{m=1}^K p\left( m|\varvec{y}_{1:j},\varvec{d}_{1:j}\right) \sum _{i = 1}^N W_{m,j}^i \\&\times u\left( \varvec{d},z_{m,j}^i| \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) , \end{aligned}$$

where $u({\varvec{d}},z_{m,j}^i| \varvec{y}_{1:j}, \varvec{d}_{1:j})$ is approximated by forming a particle approximation (via importance sampling) to the posterior distribution where $z_{m,j}^i$ (and $\varvec{d}$) are supposed observed data. That is, in the case of model uncertainty,

$$\begin{aligned}&u\left( \varvec{d},z_{m,j}^i| \varvec{y}_{1:j}, \varvec{d}_{1:j}\right) \\&\quad = 1\bigg /\sum _{l=1}^K \log \text{ trace }~\left( \text{ VAR }[\varvec{\theta }_l |\varvec{y}_{1:j}, z_{m,j}^i, \varvec{d}_{1:j}, \varvec{d}, M=l]\right) . \end{aligned}$$

5 Examples

Data have been collected on sheep which have been treated with ECMO, and have been modelled previously by Ryan et al. (2014). Each sheep was subjected to ECMO for 24 hours and infused with various antibiotic drugs. Blood samples were then collected at various times. In the original studies, Davies et al. (2009) and Shekar et al. (2013) were interested in the PK profile of antibiotic drugs in healthy sheep receiving ECMO for 24 hours as it is known that drugs are absorbed in the circuitry of ECMO. We propose to re-design this study to minimise the uncertainty about population PK parameters such that differences between PK profiles for ECMO versus non-ECMO sheep can be investigated.

The general form of the models considered in Ryan et al. (2014) and in this paper are as follows. Let the time of blood samples in minutes for sheep j (where each sheep was considered as a block) be denoted as $d_j = (d_{1j},d_{2j})$, where the possible sampling times available for blood collection are:

$$\begin{aligned} \left[ \begin{array}{cc} 6 &{} 15 \\ 15 &{} 30 \\ 30 &{} 45 \\ 45 &{} 60 \\ 60 &{} 120 \\ 120 &{} 180 \\ 180 &{} 240 \\ 240 &{} 300 \\ 300 &{} 360 \end{array}\right] . \end{aligned}$$

That is, two repeated measures are taken on each sheep, and the design problem is to choose which two sampling times (that is, which row of the above matrix) to actually use to collect plasma samples. Then

$$\begin{aligned}&y_j \sim MVN\left( g\left( \varvec{\mu }_j,d_j\right) ,\sigma ^2\text{ diag }~g\left( \varvec{\mu }_j, {d}_j\right) ^2\right) ,\\&\varvec{b}_j \sim MVN\left( \varvec{0},\varvec{\varOmega }\right) ,~~ \varvec{\mu }_j = \varvec{\mu } + \varvec{b}_j, \end{aligned}$$

with $\varvec{\mu }_j$ defined later, and priors

$$\begin{aligned}&\varvec{\mu } \sim MVN\left( \varvec{\delta },\varvec{\varSigma }\right) ,~\text{ for }\, \varvec{\delta }\hbox { and }\varvec{\varSigma }\hbox { known}\\&\varvec{\varOmega } \sim InvWish\left( \varvec{\varPsi },\nu \right) ,~\text{ for }\,\varvec{\varPsi }\, \hbox {and }\nu ~\hbox {known}\\&\log \sigma \sim N(a,b), \text{ for } a\hbox { and }b\hbox { known}. \end{aligned}$$

In both of the examples that follow, we assumed the broad spectrum antibiotic meropenem was administered to 10 sheep which were on ECMO. Meropenem was delivered as a single, IV bolus dose of 500 mg ($D = 500$), infused over 30 minutes ($Tinf=30$). The design problem was to sequentially determine the optimal times to collect blood samples in plasma from 10 sheep in order to precisely estimate population PK parameters. We considered Bayesian A-optimality for this purpose, and, as a comparison, we also considered a random design (selects sampling times at random). To investigate the properties of the utility functions, 500 trials were simulated with each utility used to select the sampling times. As this is a sequential design problem, data needed to be ‘collected’ once an optimal design for a given batch or block was found. This was facilitated by generating data from an assumed model; the parameter values of which were chosen as the modes of the prior distributions for a given model. Utility values under Bayesian A-optimality were recorded for all trials, and the chosen sampling times were also recorded. These results were then used to compare the utilities.

In the first example, we explore the proposed methods for approximating the likelihood in terms of the estimated likelihood weights and the optimal sampling times selected. The results from this investigation will be used to determine which approximation will be used in the subsequent simulation studies. In these studies, we use $N=1000$ particles and $Q=1000$ integration nodes for both examples. Further, $R_m$ is set to 10 and 20 for the models introduced in the first and second examples, respectively.

Throughout these examples, the Q evaluations of the conditional likelihood for the approximation of Eq. (1) were performed on a GPU. For a given approximation, this requires evaluating the conditional likelihood Q times for each of the N particles yielding $N\times Q$ times in total, for each model considered. With the number of particles N being in the interval $10^2-10^5$ and Q the number of conditional likelihood evaluations per particle of the order of $10^3$, it is obvious that there is substantial gain in computational speed by evaluating these likelihoods in parallel. This approach is implemented in CUDA (NVIDIA 2012) via the MATLAB CUDA API (MATLAB 2013). The complete SMC algorithm is implemented in MATLAB with a mex function written in CUDA to evaluate the approximation to the likelihood using the GPU. This implementation is compared to C code compiled and called in a similar manner. The resulting code for implementing these approaches is available upon request.

5.1 Example 1: Comparison of approximations to the likelihood

Initially, we assumed that a one-compartment infusion model was appropriate to describe the metabolism of meropenem. This model can be described as follows:

$$\begin{aligned} g\left( \varvec{\mu }_j, d_j\right) = \left\{ \begin{array}{ll} \frac{D}{Tinf}\frac{1}{k_jv_j}\left( 1-\exp \left( -k_j d_j\right) \right) ,&{} \text{ for } d_j\le Tinf \\ \frac{D}{Tinf}\frac{1}{k_jv_j}\left( 1-\exp \left( -k_jTinf\right) \right) &{} \\ \quad \exp \left( -k_j\left( d_j-Tinf\right) \right) ,&{} \text{ otherwise } \end{array}\right. \end{aligned}$$

where $(k_j,v_j) = \exp (\varvec{\mu }_j)$.

Prior information about parameter values was based on the results from Ryan et al. (2014) with;

$$\begin{aligned} \varvec{\delta } = (-3.26,8.94), \varvec{\varSigma } = 0.01\varvec{I}, \varvec{\varOmega } = \left[ \begin{array}{rr} 0.0071 &{} -0.0057\\ -0.0057 &{} 0.0080 \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \varvec{\varPsi } = 0.02\varvec{I}, \nu = 5, a = -2.3, b = 0.5 \text{ and } \sigma = 0.1. \end{aligned}$$

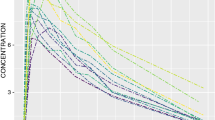
The prior predictive distribution under this model is shown in Fig. 1. One can observe that the maximum concentration is reached at 30 mins (the infusion time), and that the variability is largest here primarily because proportional residual variability was assumed. Further, it appears that the drug will have been eliminated from plasma 200 mins after the infusion has started.

Fig. 1

Prior predictive plot for the one-compartment infusion model as described in Section 6.1 based on 500 simulations

Fig. 2

Distribution of approximate likelihood weights as given by standard MC, RQMC, LIS and LIS+RQMC for a simulated trial on 10 sheep (plots (a) to (j) respectively) with $N = 500$ and $Q = 1000$

Fig. 3

Comparison of approximate expected utility values for Bayesian A-optimality as given by standard MC, RQMC, LIS and LIS+RQMC for a simulated trial on 10 sheep (plots (a) to (j) respectively) with $N = 500$ and $Q = 1000$

We start by investigating the four approximations of the likelihood proposed in this paper. A trial of 10 sheep was simulated (with $N = 500$ and $Q = 1000$). Each time new data were observed, the likelihood weights from each of the four approximations were evaluated and recorded. These weights are shown in Fig. 2. The likelihood weights as given by all four approximations appear to agree well for the first 7 sheep, with some differences becoming apparent for the 8th, 9th and 10th sheep. There appears to be no differences between the likelihood weights for the two Laplace methods, in general, with some differences seen when considering MC and RQMC. We investigate these approximation methods further by comparing the estimated expected values of the Bayesian A-optimality utility for different designs.

To compare estimates of the expected Bayesian A-optimality utility, another trial of 10 sheep was simulated. Each time an optimal design needed to be determined, all four approximation methods were run and the expected Bayesian A-utility values for each proposed design were recorded. These expected utility values are shown in Fig. 3 for all four approximation methods. In general, there is a linear relationship between the expected utility values for all methods. Importantly, all four methods find the same design as being optimal for all 10 sheep. It seems for our purposes (that is, our design space, example, etc) that any of the considered methods could be used to select the optimal designs.

We now need to choose which approximation method to run in the examples that follow. In terms of choosing the optimal designs, all four methods appear similar. So then the choice between the methods will be based on the variability of the likelihood weights. To more comprehensively compare the variability of the likelihood weights between the methods, the ESS values of particle sets for the four approaches were compared. This involved running additional simulation studies of 500 trials each of 10 sheep with MC, RQMC, LIS and then LIS+RQMC being used to approximate the likelihood weights. However, in order for the comparison of ESS values to be deemed reasonable, the sampling times and subsequent data generated in the sequential design process were fixed. This means that the ESS values from each approximation method can be compared as they are based on the same target distributions. These comparisons are shown in Figs. 4a–d for MC compared to RQMC and 5a–d for MC compared to LIS, for $Q = 10, 100, 500$ and 1000. The plots for MC compared with LIS+RQMC are omitted as the results are similar to the comparison of MC and LIS.

Fig. 4

Comparison of ESS as given by standard MC and RQMC for 500 simulated trials of 10 sheep with $N = 1000$ and $Q = 10, 100, 500$ and 1000 for plots (a)–(d), respectively

Fig. 5

Comparison of ESS as given by standard MC and LIS for 500 simulated trials of 10 sheep with $N = 1000$ and $Q = 10, 100, 500$ and 1000 for plots (a)–(d), respectively

From Fig. 4, we can see that overall there seems to be a one-to-one relationship between the ESS values from MC and RQMC, with the values become less variable as Q increases. Initially, there does not appear to be much of a difference between the ESS values. However, we investigated these values further by considering the number of times (out of 5000) RQMC gave an ESS value greater than MC. This yielded the following percentages 56.0, 55.9, 49.0 and 53.1 % for $Q = 10, 100, 500$ and 1000, respectively. The results are mixed but for $Q = 10, 100$ and 1000, RQMC gave better ESS values with the average (median) difference being 11.6 (6.0), 4.2 (1.86) and 0.8 (0.3), respectively. This suggests that there are potentially quite reasonable gains when using RQMC. Of course, when $Q = 500$, MC gave better ESS values more often. This suggests that the performance of RQMC may be implementation specific. In fact, performance also varies depending upon the value of $v_k$ chosen in Algorithm 1. In our work, we arbitrarily selected $v_k = [0.1, 0.1]$, where $v_k$ could in actual fact be chosen to minimize a measure of discrepancy (Dick et al. 2004; Munger et al. 2012). This could provide improved ESS values for RQMC.

From Fig. 5, again it appears that overall there is a one-to-one relationship between the ESS values. However, the percentage of times (out of 5000) LIS gave an ESS value greater than MC was 53.9, 50.7, 50.1 and 50.5 % for $Q = 10, 100, 500$ and 1000, respectively. Further, LIS gave better ESS values than MC with the average (median) difference being 13.0 (3.5), 1.4 (0.1), 0.5 (0.02) and 0.03 (0.04) for $Q = 10, 100, 500$ and 1000, respectively. When comparing RQMC and LIS, it appears that RQMC yields the smallest variability of the likelihood weights (when $Q = 10, 100$ and 1000). Therefore, this method will be used in the examples that follow. We note also that the computation time when using RQMC when compared to LIS is significantly reduced as the need to numerically find the mode a large number of times poses considerable computational burden. In fact, the computation time required for RQMC is only incrementally larger than that as given by standard MC.

5.2 Example 1 continued: Bayesian A-optimality for one compartment pharmacokinetic model

The Bayesian A-optimal sampling times for each of the 10 sheep over 500 simulated studies are shown in Fig. 6, where the figure shows the empirical probability distribution of the first of the two selected sampling times in each sheep. It is clear that early sampling times are prefered with the majority of sampling times being selected before 30 mins. Indeed, for the first 4 sheep, sampling times [6, 15] mins were selected 100 % of the time. Larger sampling times were selected for sheep near the end of the trial.  Overall, it appeared that design selection was largely driven by the parameter which was most variable. In most cases, this was the parameter representing the volume of distribution.

Fig. 6

Empirical probability distribution of sampling times selected in 500 simulated trials of 10 sheep for the one-compartment infusion model under Bayesian A-optimality. Note: Only the first sampling time has been plotted

Fig. 7

Utility values for the 500 simulated trials for Bayesian A-optimality and the random design

Table 1 Average run times (s) for the evaluation of the likelihood under different implementations for data from a single block for the one compartment and two compartment infusion models

Utility values for the 500 simulated trials for Bayesian A-optimality and the random design are shown in Fig. 7. It can be seen that there can potentially be over a 10 fold improvement in the (inverse of the) total or average variance of the parameters when using the Bayesian A-optimality as opposed to the random design. It can also be seen that there are occasions where the random design may have yielded a higher utility value than A-optimality. This is presumably because, given the small number of potential designs to use for data collection, by chance, the random design has selected sampling times that lead to precise parameter estimates. Further, varibility in the simulated data may also contribute to the occurrence of such instances. Notably, this overlap is only seen in about the lower 50th percentile of the utility values for the Bayesian A-optimality utility function suggesting that this utility is in general outperforming random selection.

5.3 Example 1 continued: Comparison of run times

Of interest are the run times for evaluating the likelihood under different implementations. These are shown for implementations in C and CUDA (GPU) for this example in Table 1 and Fig. 11a. The run times shown are for the evaluation of the likelihood, averaged over 25 evaluations. The results shown in Fig. 11 are just the log base 10 of those shown in Table 1. These runs were performed on a Windows desktop computer with an Intel(R) Xeon(R) CPU E5-1620 0 @ 3.60 GHz processor and a NVIDIA Quadro 2000 1GB GPU. Further, we note that the evaluation of the likelihood requires the generation of random numbers which can contribute significantly to run times. In all run times shown, the required random numbers were generated before the timed likelihood call. In regards to the implementations, it is believed that the comparisons between the C and CUDA implementations are true representations of what can be gained through using a GPU. This is because the CUDA implementation is essentially the same C code but compiled to run on a GPU. Hence, it is essentially the hardware that is being compared.

From Table 1 and Fig. 11:

• The CUDA code runs about 18 times faster than the C code;

• There is a roughly linear increase in computing time with respect to Q for the GPU implementation;

• Increases in time are not linear with respect to N for the GPU implementation. For example, there is not a huge increase in computing time between $N = 100$ and $N = 1000$. Moreover, in general, there is about a 10 fold increase in run times when $N=100$ compared to $N = 10{,}000$;

• For the C implementations, increases in time are roughly linear with N and Q;

The reduction in computing times presented when implementing the C and CUDA code is quite reasonable, with the maximum benefits for using CUDA coming for the largest N and Q, which is the case where computational time is most expensive.

5.4 Example 2: Bayesian A-optimality for one and two compartment pharmacokinetic models

Consider an example where there is uncertainty around the form of $g( \varvec{\mu }_j, {d}_j)$. As well as the model in the first example, the following two-compartment infusion model was also contemplated:

for $(k_j,k_{12j},k_{21j},v_j) =\exp (\varvec{\mu }_j)$, where

$$\begin{aligned} A_j= & {} \frac{1}{v_j}\frac{\alpha _j - k_{21j}}{\alpha _j-\kappa _j}, \quad B_j = \frac{1}{v_j}\frac{\kappa _j-k_{21j}}{\kappa _j-\alpha _j},\\ \alpha _j= & {} \frac{k_{21j}k_j}{\kappa _j}, \\ \kappa _j= & {} \frac{1}{2}\Bigg [k_{12j} + k_{21j} - k_j \\&-\sqrt{\left( k_{12j} + k_{21j} + k_j\right) ^2 - 4k_{21j}k_j} \Bigg ]. \end{aligned}$$

Results obtained from a two compartment analysis of data from Ryan et al. (2014) were used to give the prior distribution values:

$$\begin{aligned} \varvec{\delta }= & {} \left( -2.502, 0.8326, 0.6563, 8.225\right) , \varvec{\varSigma } = 0.01\varvec{I}, \\ \varvec{\varOmega }= & {} \left[ \begin{array}{rrrr} 0.0120&{} -0.0012&{} 0.0012&{} 0.0018 \\ -0.0012&{} 0.0085&{} 0.0002&{} -0.0051 \\ 0.0012&{} 0.0002&{} 0.0104&{} 0.0046 \\ 0.0018&{} -0.0051&{} 0.0046&{} 0.0195 \end{array} \right] ,\\ \varvec{\varPsi }= & {} 0.02\varvec{I}, \nu = 7, a = -2.3, b = 0.5 \text{ and } \sigma = 0.1. \end{aligned}$$

The prior predictive distribution of this two-compartment model is shown in Fig. 8. This appears similar in shape to the one-compartment model with the peak concentration at 30 mins after the infusion has started. The additional compartment in this model yields the characteristic kink in the tail, and, in this case, there appears to be more variability around the typical response when compared to the one-compartment model.

Fig. 8

Prior predictive plot for two-compartment infusion model as described in Section 6.4 based on 500 simulations

Fig. 9

Empirical probability distribution of sampling times selected in 500 simulated trials of 10 sheep for Example 2 under Bayesian A-optimality. Note: Only the first sampling time has been plotted

Fig. 10

Utility values for each simulated trial for Bayesian A-optimality and the random design for Example 2

Fig. 11

Log base 10 of average computing times (s) for evaluating the likelihood under different implementations in: a Example 1 and b Example 2

The Bayesian A-optimal sampling times for each of the 10 sheep over 500 simulated studies are shown in Fig. 9 for when the one-compartment model was supposed responsible for the sequential data generation. Again, the plot shows the empirical probability distribution of the first of the two selected sampling times in each sheep. There appears to be differences in the selected sampling times when one allows for the possibility of a two-compartment model being responsible for data generation. There is still a perference for early sampling times, however, there are more sampling times closer to the peak concentration and sampling times far beyond this point can be observed from the first sheep (rather than from the fourth sheep as seen in the first example). The different sampling times selected betwen the two examples could highlight potential sub-optimalities that may be observed if one were to simply design for a single model when model uncertainty exists.

Figure 10 displays density plots of utility values for each of the 500 completed trials for when the Bayesian A-optimality utility was used for design selection compared to the random design. Despite the introduction of more uncertainty, in particular around the true model, one can see that Bayesian A-optimality is generally performing better than the random design. There is potentially around a threefold improvement in the (inverse of the) total or average variance of the parameters when using the Bayesian A-optimality utility. Again, there are occassions where the random design may have performed better, and this is by chance. In comparison with Example 1, the distributions of utility values, as given by Bayesian A-optimality and the random design, appear to overlap more. Presumably, this is a consequence of having more variability to deal with when constructing the designs.

This example was also re-run with the two compartment model used to generate the sequential data. This yielded similar results to those presented here when the one compartment model was used for data generation, but are omitted. This suggests that the Bayesian A-optimality utility is selecting designs that are robust to model uncertainty. Indeed, this is how the utility was constructed to perform. Robustness to such uncertainty is obviously an important characteristic of an optimal design, and our methodology extends straightforwardly to the consideration of more than two models for data generation.

Table 1 and Fig. 11b show similar run time results for the two compartment model when compared with the one compartment model, with the benefits of CUDA when compared to C reduced slightly. In this example, the CUDA code is only roughly ten times faster than the C implementation. This reduced improvement may be due to the increased model complexity, or more precisely the larger size of the instructions set required to compute the likelihood for the two compartment model. The GPU consists of a large number of light-weight processors with limited memory or register space to store instructions. When the size of the instruction set exceeds a certain limit, the GPU is no longer able to use all its processors at once, reducing the number of available processors for parallel operations; in turn reducing the computational advantages of the GPU.

6 Conclusion

In this paper, we have proposed a new pseudo-marginal SMC algorithm for sequentially designing experiments that yield batch or block data in the presence of model and parameter uncertainty when the likelihood is not analytic and has to be approximated. Our work was motivated by the need for an efficient Bayesian inference and design algorithm where data are observed sequentially, and the SMC algorithm served this purpose well. Our developments of a new pseudo-marginal algorithm have extended the use of SMC to random effects models, where we can achieve efficient estimates of important statistics such as the model evidence. With respect to implementation, a nice feature of the idealised and our new SMC algorithm is that it can be implemented in either a coarse-grained way or a fine-grained way. Thus with little effort, it can perform well on both multi-core CPUs or GPUs. In our work, computational efficiency was achieved via the use of a GPU when evaluating the approximation of the likelihood for a given model. This GPU implementation was up to 18 times faster than the C implementation, and made this research possible in a reasonable amount of time. We argue that the run time comparisons between C and CUDA are reasonably fair comparisons as the code and computing language for running both implementations is essentially the same.

We considered standard MC, RQMC, LIS and LIS+RQMC integration techniques for approximating the likelihood. All approaches produced comparable results for design selection, however, differences were observed in the estimated likelihood weights. These differences were explored further where it was found that, under certain implementations, RQMC provides the larger ESS values overall. As such, RQMC was proposed for use in the examples, and we note that this method is generally faster to implement when compared with LIS and LIS+RQMC. However, other approaches may prove more useful here. Indeed, in terms of optimal experimental design, it may not be necessary to consider an exact-approximate algorithm for design selection. For example, one could consider deterministic approaches for fast posterior approximations such as those given by an integrated-nested Laplace approximation (Rue et al. 2009) or variational methods (Beal 2003). We plan to investigate this in future research.

We considered an important PK study in sheep being treated with ECMO, and results suggested that prolonged use of ECMO may not be required for the estimation of PK parameters. Reduced trial lengths may provide more ethical studies while not compromising experimental results.

In our PK examples, the experimental aims reflected precise parameter estimation with the possibility of model uncertainty but other aims (and therefore utility functions) may be of interest. For example, experimenters may be more interested in determining the form of the model, that is, model discrimination, and a utility function based on mutual information has been considered in previous research for this purpose (Drovandi et al. 2014). However, implementation was shown to be computationally challenging, even for fixed effects models. We note that the methodology presented here can be applied to find designs for this purpose within a mixed effects setting, and is an avenue for future research. It may also be of interest to not only derive designs for model discrimination, but also for the precise estimation of parameters. Dual objective or compound utility functions could be considered for this purpose.

A limitation of our implementation is the discretisation of the design space. On-going research in this area is in the consideration of Gaussian Processes to model the expected utility surface/s (Overstall and Woods 2015). Such models are known to be powerful nonlinear interpolation tools, and therefore could prove useful here. The choice of design points to ‘observe’ the expected utility is a design problem within itself. Of further interest would be the choice of covariance function.

We would also like to mention that there are further opportunities to reduce run times. In particular, running the actual SMC (inference) algorithm in parallel would certainly significantly reduce computing times. Moreover, as proposed designs are independent, then the design selection phase of the algorithm could be run in parallel (for example, one thread per proposed design). This may also prove useful in overcoming the limitation of discretising the design space. One could also potentially improve run times by adopting a different kernel in the move step. For example, Liu and West (2001) propose a kernel which, by accepting all proposed parameters, preserves the first two moments of the target distribution. In our implementation, this would therefore reduce our move step iterations from $R_m$ to one, and has been used in sequential design previously (Azadi et al. 2014). This approximation would work well if the posterior distributions were well approximated by mixtures of Gaussian distributions. The number of likelihood evaluations could also be reduced by considering a Markov kernel (Del Moral et al. 2006). For this kernel, the normalising constant needs to be estimated yielding an $O(N^2)$ algorithm (as opposed to the O(N) algorithm proposed here). However, using this kernel would reduce the number of evaluations of the likelihood by a factor of $R_m$. The Liu and West (2001) kernel could be corrected for non-Gaussian posteriors by this approach or using a Metropolis-Hastings step.