Abstract
We develop a new exponential family model for permutations that can capture hierarchical structure in preferences, and that has the well known Mallows models as a subclass. The Recursive Inversions Model (RIM), unlike most distributions over permutations of n items, has a flexible structure, represented by a binary tree. We describe how to compute marginals in the RIM, including the partition function, in closed form. Further we introduce methods for the Maximum Likelihood estimation of parameters and structure search for this model. We demonstrate that this added flexibility both improves predictive performance and enables a deeper understanding of collections of permutations.








Similar content being viewed by others
Notes
We would have liked to make a direct comparison with the algorithm of Huang and Guestrin (2012), but the code is not available. Using the HG structure has the purpose to evaluate the quality of the structures found by SASearch in comparison to a given structures that was previously found to model these data reasonably well.
Followed by parameter estimation and Canonicalize.
References
Ali, A., Meila, M.: Experiments with kemeny ranking: What works when?. Mathematics of Social Sciences, Special Issue on Computational Social Choice, page (in press) (2011)
Andrews, G.: The Theory of Partitions. Cambridge University Press, Cambridge (1985)
Bartholdi, J., Tovey, C.A., Trick, M.: Voting schemes for which it can be difficult to tell who won. Soc. Choice Welf. 6(2), 157–165 (1989). (proof that consensus ordering is NP hard)
Borda, J.-C.: Mémoire sur les élections au scrutin. Hiswire de I’Academie Royale des Sciences (1781)
Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to Algorithms, 2nd edn. The MIT Press, Cambridge (2001)
Earley, J.: An efficient context-free parsing algorithm. Commun. ACM 13(2), 94–102 (1970)
Fligner, M.A., Verducci, J.S.: Distance based ranking models. J. R. Stat. Soc. B 48, 359–369 (1986)
Gormley, I.C., Murphy, T.B.: A latent space model for rank data. In: Proceedings of the 24th Annual International Conference on Machine Learning, pages 90–102, New York. ACM (2007)
Huang, J., Guestrin, C.: Riffled independence for ranked data. In: Bengio, Y., Schuurmans, D., Lafferty, J.D., Williams, C.K.I., Culotta, A. (eds.) Advances in Neural Information Processing Systems 22, pp. 799–807. Curran Associates Inc, New York (2009)
Huang, J., Guestrin, C.: Uncovering the riffled independence structure of ranked data. Electron. J. Stat. 6, 199–230 (2012)
Huang, J., Guestrin, C., Guibas, L.: Fourier theoretic probabilistic inference over permutations. J. Mach. Learn. Res. 10, 997–1070 (2009)
Huang, J., Kapoor, A., Guestrin, C.: Riffled independence for efficient inference with partial rankings. J. Artif. Intell. Res. 44, 491–532 (2012)
Joe, H., Verducci, J.S.: On the babington smith class of models for rankings. In: Fligner, M.A., Verducci, J.S. (eds.) Probability Models and Statistical Analyses for Ranking Data, pp. 37–52. Springer New York, New York, NY (1993)
Kamisha, T.: Nantonac collaborative filtering: recommendation based on order responses. In: Proceedings of the ninth ACM SIGKDD in- ternational conference on Knowledge discovery and data mining, pages 583–588, New York. ACM (2003)
Kirkpatrick, S., Gelatt, C.D., Vecchi, M.P.: Optimization by simulated annealing. Sci. 220, 671–680 (1983)
Mallows, C.L.: Non-null ranking models. Biom. 44, 114–130 (1957)
Mandhani, B., Meila, M.: Better search for learning exponential models of rankings. In: VanDick, D., Welling, M. (Eds.), Artificial Intelligence and Statistics AISTATS, number 12 (2009)
Manilla, H., Meek, C.: Global partial orders from sequential data. In: Proceedings of the Sixth Annual Confrerence on Knowledge Discovery and Data Mining (KDD), pages 161–168 (2000)
Meek, C., Meila, M.: Recursive inversion models for permutations. In: Advances in Neural Information Processing Systems, pages 631–639 (2014)
Meilă, M., Phadnis, K., Patterson, A., Bilmes, J.: Consensus ranking under the exponential model. In: Parr, R., Van den Gaag, L. (Eds.), Proceedings of the 23rd Conference on Uncertainty in AI, volume 23 (2007)
Schalekamp, F., van Zuylen, A.: Rank aggregation: Together we’re strong. In: Finocchi, I., Hershberger, J. (Eds.), Proceedings of the Workshop on Algorithm Engineering and Experiments, ALENEX 2009, New York, New York, USA, January 3, 2009, pages 38–51. SIAM (2009)
Stanley, R.P.: Enumerative Combinatorics: Volume 1, 2nd edn. Cambridge University Press, Cambridge (2011)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Figures
Supplementary Figures
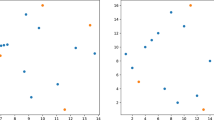
Figure 8 shows an example of the type of structure used and found in Sect. 6.1, chosen from \(N=1000\) as an example containing model mismatch.
The left model represents the true model and parameters from which a sample was drawn, with the marginal \({\bar{Q}}(\tau (\mathbf {\theta }))\). The right model represents the found structure and parameters using the same search parameters as the experiments, along with the sample \({\hat{Q}}\) that was used to fit the model. The Frobenius norm of the difference between the true \({\bar{Q}}(\tau (\mathbf {\theta }))\) and \({\hat{Q}}\) is \(\Vert {\bar{Q}}(\tau (\mathbf {\theta }))-{\hat{Q}}\Vert _F=0.0828\), while the norm between \({\hat{Q}}\) and the marginal \({\bar{Q}}({\hat{\tau }}(\hat{\mathbf {\theta }}))\) (not shown) is only 0.0322, and \(\Vert {\bar{Q}}(\tau (\mathbf {\theta }))-{\bar{Q}}({\hat{\tau }}(\hat{\mathbf {\theta }}))\Vert _F\) is 0.0785. This lack of ability to identify the true model from the sample is likely a consequence of two adjacent values of \(\theta _i\) being very (0.6924 and 0.762). This can be seen playing out in the misplacement of item \(e_6\). Figure 9 shows the training log-likelihoods, in an otherwise identical format to the plots found in Fig. 4. We can see that the alternate initialization has little influence on the final log-likelihood, with many instances finding an identical model to the runs using a more nuanced starting ranking. Similarly, and unsurprisingly, we see the RIM model as a clear winner when comparing testing likelihoods, largely due to the improved flexibility over other models. It is likely that the Rank Inversion model would have fitted the training data better than the \(\mathtt HG\) model we see here, which only uses the structure of the found Rank Inversion models but constrains them to the exponential inversion model of shuffle likelihoods.
Rights and permissions
About this article
Cite this article
Meilă, M., Wagner, A. & Meek, C. Recursive inversion models for permutations. Stat Comput 32, 54 (2022). https://doi.org/10.1007/s11222-022-10111-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-022-10111-4