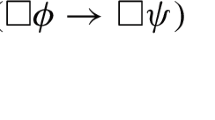Abstract
I challenge a claim that seems to be made when nominalists offer reformulations of the content of mathematical beliefs, namely that these reformulations are accessible to everyone. By doing so, I argue that these theories cannot account for the mathematical knowledge that ordinary people have. In the first part of the paper I look at reformulations that employ the concept of proof, such as those of Mary Leng and Ottavio Bueno. I argue that ordinary people don’t have many beliefs about proofs, and that they are not in a position to acquire knowledge about proofs autonomously. The second part of the paper is concerned with other reformulations of content, such as those of Hartry Field and Stephen Yablo. There too, the problem is that people are not able to acquire knowledge of the reformulated propositions autonomously. Ordinary people simply do not have beliefs with the kind of content that the nominalists need, for their theory to account for the mathematical knowledge of ordinary people. All in all then, the conclusion is that a large number of theories that suggest reformulations of mathematical content yield contents that are inaccessible for most people. Thus, these theories are limited, in that they cannot account for the mathematical knowledge of ordinary people.
Similar content being viewed by others
Notes
Basturk describes students with capacities of this kind. “The findings have also showed that the students’ studying methods for exams based on imitative reasoning which can be described as a type of reasoning built on copying task solution (or proof), for example by looking at a textbook or course notes proof or through remembering a proof algorithm. The students said that they tried to memorise proofs by rewriting them many times before exams. Moreover they had a lack of self-confidence in constructing a proof never seen. It can be asserted that they employed memorised reasoning (or proving), one of the types of imitative reasoning, which consists of recalling a complete answer (proof) by memory or writing down (or saving) the proof.” (Basturk 2010, p. 295)
Almeida describes students with this kind of capacity. “The evidence reveals that pupils’ views of proof are generally empirical. Apart from a few, most pupils view justification as verifying by empirical evidence.” (Almeida 2001, p. 59) “They appear to believe that the consistency of a set of confirmations is sufficient to justify statements, that such evidence will provide a ‘guarantee from counterexamples’ ...Typical perceptions of these pupils about justification or explanation are: ‘I don’t know how to justify it, it’s just that I can give you more examples.’ ‘I don’t know how to explain it, the only thing is to give evidence to prove it, that should (\(\ldots \)) speak for itself.’ ‘I don’t know how I’d go about actually explaining it to them unless just (by) giving them more evidence.” (Almeida 2001, pp. 58–59).
This doesn’t seem to be a view held by everyone discussed here, although there is no explicit discussion of the exact requirements on a philosophy of mathematics. Field in particular seems to care mostly about professional mathematicians. Yet, that doesn’t mean that his theory shouldn’t account for this.
Note, though, that Field (1980) isn’t presenting a view here on which the content of our mathematical beliefs is reformulated, in the way in which the theories I argue against here do so. So, the suggestion here should not be understood as reflecting a view that Field actually held.
My thanks to an anonymous reviewer for pointing out that Balaguer’s platonist theory can escape the worries in this way.
References
Almeida, D. (2001). Pupils’ Proof Potential. International Journal of Science and Mathematics Education, 32(1), 53–60.
Azzouni, J. (1994). Metaphysical myths, mathematical practice. Cambridge: Cambridge University Press.
Azzouni, J. (2011). Nominalistic content. In C. Celluci, E. Grosholz, & E. Ippoliti (Eds.), Logic and knowledge (pp. 33–51). Newcastle upon Tyne: Cambridge.
Azzouni, J. (2012). Taking the easy road out of dodge. Mind, 121(484), 951–965.
Balaguer, M. (1995). A platonist epistemology. Synthese, 103(3), 303–325.
Balaguer, M. (2009). Fictionalism, theft, and the story of mathematics. Philosophia Mathematica (III), 17, 131–162.
Basturk, S. (2010). First-year secondary school mathematics students’ conceptions of mathematical proofs and proving. Educational Studies, 36(3), 283–298.
Bueno, O. (2009). Mathematical fictionalism. In O. Buena & Ø. Linnebo (Eds.), New waves in the philosophy of mathematics (pp. 59–79). Basingstoke: Palgrave Macmillan.
Bueno, O. (2011). Logical and mathematical knowledge. In S. Bernecker & D. Pritchard (Eds.), Routledge companion to epistemology. New York: Routledge.
Buijsman, S. (2016). Philosophy of mathematics for the masses. PhD Thesis, Stockholm University.
Burge, T. (1979). Individualism and the mental. Midwest Studies in Philosophy, 4(1), 73–121.
Field, H. (1980). Science without numbers. New York: Blackwell.
Field, H. (1989). Realism, mathematics and modality. Oxford: Blackwell.
Goldberg, S. (2002). Do anti-individualistic construals of propositional attitudes capture the agent’s conceptions? Noûs, 36(4), 597–621.
Goldberg, S. (2007). Anti-individualism: mind and language, knowledge and justification. Cambridge: Cambridge University Press.
Goodman, N., & Quine, W. V. O. (1947). Steps toward a constructive nominalism. The Journal of Symbolic Logic, 12(4), 105–122.
Harel, G. (2002). The development of mathematical induction as a proof scheme: A model for DNR-based instruction. In S. Campbell & R. Zaskis (Eds.), Learning and teaching number theory: Research in cognition and instruction. Westport: Greenwood Press.
Leng, M. (2007). What’s there to know? A fictionalist account of mathematical knowledge. In M. Leng, A. Paseau, & M. Potter (Eds.), Mathematical knowledge (pp. 83–108). Oxford: Oxford University Press.
Muis, K. (2004). Personal epistemology and mathematics: A critical review and synthesis of research. Review of Educational Research, 74(3), 317–377.
Palla, M., Potari, D., & Spyrou, P. (2012). Secondary school students’ understanding of mathematical induction: Structural characteristics and the process of proof construction. International Journal of Science and Mathematics Education, 10, 1023–1045.
Peacocke, C. (1992). A study of concepts. Cambridge, Massachutes: MIT Press.
Schwitzgebel, E. (2014). Belief, The Stanford Encyclopedia of Philosophy (Spring 2014 Edition), E.N. Zalta (ed.). http://plato.stanford.edu/entries/belief/.
Weber, K., Inglis, M., & Mejia-Ramos, J. P. (2014). How mathematicians obtain conviction: Implications for mathematics instruction and research on epistemic cognition. Educational Psychologist, 49(1), 36–58.
Yablo, S. (2001). Go figure: A path through fictionalism. Midwest Studies in Philosophy, XXV, 72–102.
Acknowledgments
I wish to thank Chris Kelp, Peter Pagin, Marco Panza, Dag Westerståhl, Åsa Wikforss and two anonymous referees for this journal for very helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is a revised version of material from my PhD Thesis, Buijsman (2016).
Rights and permissions
About this article
Cite this article
Buijsman, S. Accessibility of reformulated mathematical content. Synthese 194, 2233–2250 (2017). https://doi.org/10.1007/s11229-016-1054-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1054-8