Zone-based load balancing in two-tier heterogeneous cellular networks: a game theoretic approach

Abstract

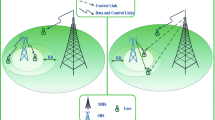
In this paper, load balancing in two-tier cellular networks is investigated. The network under-study is divided into several zones. The first tier of each zone includes a heavy-loaded Macrocell (i.e., the central cell) and its neighboring cells. The second tier includes Picocells in the area of the zone. We model the load balancing problem in each zone as a Cournot game where the optimal load distribution of each cell is the Nash Equilibrium Solution (NES) of the game. Since the actual load of each cell depends on the initial placement of users and their mobility pattern, a load balancing algorithm called Weighted Distributed Heterogeneous Zone based Load Balancing (W-DHZLB) is proposed which transfers loads between over-loaded and under-loaded cells aiming at approximating the obtained NES. In order to avoid ping-pong effect during hand-overs, inner users are given a higher priority to join a Macrocell compared to the users locating on the edge of the same Macrocell. Therefore, when loads are transferred to a Picocell, it is more likely one of the internal users of the corresponding Macrocell rather than users residing in the neighboring Macrocell. The proposed algorithm reduces the risk of epidemic unbalanced load distribution in heterogeneous networks. Simulation results show that W-DHZLB outperforms a previous load balancing algorithm in the literature.

Appendices

Appendix A: Finding NESs points of GLB game model

Recalling that in Sect. 4.1, the mathematical form of Game is as below:

$$\begin{aligned} \begin{array}{l} \max \quad u\left( {l_i ,l_{-i} } \right) =\left( {p\left( {l_i ,l_{-i} } \right) -c} \right) .l_i \\ s.t\left\{ {{\begin{array}{c} {l_i <l_{th} } \\ {l_i^{\min } \le l_i \le l_i^{\max } } \\ \end{array} }} \right. \\ \end{array} \end{aligned}$$

(A.1)

Also we know that the $NESs\left( {l_i^*,l_{-i}^*} \right)$ of our GLB game should satisfy the following condition:

$$\begin{aligned} u_i \left( {l_i^*,l_{-i}^*} \right) \ge u_i \left( {l_i ,l_{-i}^*} \right) \quad for\,{l_i \in L_i} \end{aligned}$$

(A.2)

We use the prove approach same as in reference [22]. As discussed in Sect. 4, our proposed game is done in 2 levels. The only difference between two games is in function $p\left( {l_i ,l_{-i} } \right)$ . In the following, proof of NESs existence and NESs load for the first game (Macrocells layer) is presented. The proof process for the second game can be done in the same way.

We must show that $NESs\left( {l_i^*,l_{-i}^*} \right)$ exists for our GLB_level2 game. In addition, due to the multi-constraint conditions in (A.1), we have three cases to investigate the existence of NESs.

• Case 1$l_{th} <l_i^{\min }$. In this case the threshold is lower than the minimum allowed load of cell i, therefore load balancing process is never triggered for cell i. Hence, in this case the answer space would be empty [22].

• Case 2 If $l_i^{\min }<l_{th} <l_i^{\max }$ then (A.1) can be rewritten as:

  $$\begin{aligned} \begin{array}{ll} {\max }&{} u\left( {l_i ,l_{-i} } \right) =\left( {p(l_i ,l_{-i} )-c} \right) \hbox {. }l_i \\ {s.\,t}&{} \left\{ {l_i^{\min } \le l_i \le l_{th}} \right. \\ \end{array} \end{aligned}$$

  (A.3)

• Case 3 If $l_i^{\max } \le l_{th}$ then (A.1) can be rewritten as:

  $$\begin{aligned} \begin{array}{ll} {\max }&{} {u\left( {l_i ,l_{-i} } \right) =\left( {p\left( {l_i ,l_{-i} } \right) -c} \right) \hbox {. }l_i } \\ {s.t}&{} {\left\{ {l_i^{\min } \le l_i \le l_i^{\max } } \right. } \\ \end{array} \end{aligned}$$

  (A.4)

For Case 2, we use the Lagrange multipliers to relax the constrained conditions in (A.3), i.e.

$$\begin{aligned} \xi _i \left( {l_i ,l_{-i} } \right)= & {} \left( {\left( {p_i \left( {l_i ,l_{-i} } \right) -c} \right) .l_i } \right) -\left( {\lambda _i .\left( {l_i^{\min } -l_i } \right) } \right) \nonumber \\&-\left( {\rho _i .\left( {l_i -l_{th} } \right) } \right) \end{aligned}$$

(A.5)

Now, we derive the first-order partial derivative with respect to $l_{i}$, i.e.,

$$\begin{aligned} \frac{\partial \xi _i \left( {l_i ,l_{-i} } \right) }{\partial l_i }= & {} \left( {\frac{\partial p_i \left( {l_i ,l_{-i} } \right) }{\partial l_i }.l_i } \right) +\left( {p_i \left( {l_i ,l_{-i} } \right) -c} \right) \nonumber \\&+\lambda _i -\rho _i \end{aligned}$$

(A.6)

Recalling (3) in Sect. 4.1, the following equation can be derived:

$$\begin{aligned} \frac{\partial p_i \left( {l_i ,l_{-i} } \right) }{\partial l_i }=- 1 \end{aligned}$$

(A.7)

Then we have:

$$\begin{aligned} \frac{\partial \xi _i \left( {l_i ,l_{-i} } \right) }{\partial l_i }= & {} -l_i +\left( {a-\left( {\alpha .\left( {\sum _{\begin{array}{c} j=1, \\ j\in macrocell, \\ j\ne i \\ \end{array}}^n {l_j } } \right) } \right) }\right. \nonumber \\&\left. {-\left( {\beta .\left( {\sum _{\begin{array}{c} k=1, \\ k\in picocell \\ \end{array}}^m {l_k \hbox { }} } \right) } \right) -l_i -c} \right) +\lambda _i -\rho _i\nonumber \\= & {} -\hbox { }2.l_i +\left( {a-\alpha .\left( {\sum _{\begin{array}{c} j=1, \\ j\in macrocell, \\ j\ne i \\ \end{array}}^n {l_j } } \right) }\right. \nonumber \\&\left. {-\left( {\beta .\sum _{\begin{array}{c} k=1, \\ k\in picocell \\ \end{array}}^m {l_k \hbox { }} } \right) -c+\lambda _i -\rho _i } \right) \nonumber \\ \end{aligned}$$

(A.8)

Let (A.8) be equal to zero, and we have:

$$\begin{aligned}&-2.l_i +\left( {a-\alpha .\left( {\sum _{\begin{array}{c} j=1, \\ j\in macrocell, \\ j\ne i \\ \end{array}}^n {l_j } } \right) }\right. \nonumber \\&\quad \left. {-\left( {\beta .\sum _{\begin{array}{c} k=1, \\ k\in picocell \\ \end{array}}^m {l_k \hbox { }} } \right) -c+\lambda _i -\rho _i } \right) =0 \end{aligned}$$

(A.9)

Solving (A.9), the load strategy is computed as

$$\begin{aligned} l_i =\frac{\left( {a-c} \right) -\left( {\alpha .\sum \nolimits _{\begin{array}{l} j=1, \\ j\in macrocell, \\ j\ne i \\ \end{array}}^n {l_j } } \right) -\left( {\beta .\sum \nolimits _{\begin{array}{l} k=1,\hbox { } \\ k\in picocell \\ \end{array}}^m {l_k } } \right) +\lambda _i -\rho _i }{2}\nonumber \\ \end{aligned}$$

(A.10)

In order to simplify the analysis of NES existence, we assume that Note that the value of ($a-c)$ has no impact on achieving closed form of our NES solution [22]. Finally, the closed form Nash equilibrium is:

$$\begin{aligned} l_i =\hbox { }\frac{\frac{\alpha }{8}.\left( {\sum \nolimits _{\begin{array}{l} j=1, \\ j\in macrocell, \\ j\ne i \\ \end{array}}^n {l_j } } \right) +\left( {\frac{\beta }{8}.\sum \nolimits _{\begin{array}{l} k=1, \\ k\in picocell \\ \end{array}}^m {l_k } } \right) +\lambda _i -\rho _i }{2-\hbox { }\frac{9}{8}.\alpha }\nonumber \\ \end{aligned}$$

(A.11)

For Case 3, a closed form Nash equilibrium can be derived similar to that in Case 2. Similarly, the closed form for NESs of the GLB_level 2 game is also calculated. And we have:

$$\begin{aligned} l_i =\hbox { }\frac{\left( {\frac{1}{8}\gamma .\sum \nolimits _{\begin{array}{l} k=1, \\ k\ne i, \\ k\in picocell \\ \end{array}}^m {l_k } } \right) +\hbox { }\left( {\frac{1}{8}\varphi .l_{j(parentMacrocell)} } \right) +\hbox { }\lambda _i -\rho _i }{\frac{7}{8}}\nonumber \\ \end{aligned}$$

(A.12)

Now we must prove that our NES is unique and optimal. In [22], it is proved that if derivation of $\xi _i (l_i ,l_{-i} )$ with respect to $l_{i}$, $l_{j}$ was smaller than zero, then it can be said that the game is sub-modular and it has a unique NES. In our GLB game, for Macrocells we have:

$$\begin{aligned} \frac{\partial ^{2}\xi _i \left( {l_i ,l_{-i} } \right) }{{\begin{array}{ll} {\partial l_i }&{} {\partial l_j } \\ \end{array} }}= & {} \frac{-\alpha .\sum \nolimits _{\begin{array}{l} j=1, \\ j\in macrocell, \\ j\ne i \\ \end{array}}^n {l_j } }{\partial l_j }\nonumber \\= & {} {\begin{array}{ll} {-\alpha }&{} {\left( {n-1} \right) } \\ \end{array} }\le 0{\begin{array}{ll} &{} {for(n\in Macrocell)} \\ \end{array}}\nonumber \\ \end{aligned}$$

(A.13)

And in Picocells:

$$\begin{aligned}&\frac{\partial ^{2}\xi _i \left( {l_i ,l_{-i} } \right) }{{\begin{array}{ll} {\partial l_i }&{} {\partial l_k } \nonumber \\ \end{array} }}\\&\quad =\hbox { }\frac{\left( {-\gamma .\sum \nolimits _{\begin{array}{l} k=1, \\ k\ne i, \\ k\in picocel \\ \end{array}}^m {l_k } } \right) -2l_i -\varphi l_{j(ParentMacrocell)} }{\partial l_k }\nonumber \\&\quad ={\begin{array}{llll} {-\gamma }&{} {\left( {m-1} \right) }&{} \le &{} {0{\begin{array}{ll} &{} {for(m\in Picocell)} \\ \end{array} }} \\ \end{array}} \end{aligned}$$

(A.14)

We can conclude that our NES in both Macrocell and Picocell layers is unique. For proving optimality of NES, we can say that $\frac{\partial ^{2}\xi _i (l_i ,l_{-i} )}{\partial ^{2}l_i }={-2} \le 0$ is valid for NES in both Macrocells and Picocells. Therefore it can be concluded that our NESs are optimal and the close form of them can be found in (A.11) and (A.12).

Using Eqs. (A.11) and (A.12), the optimum load will be determined in each cell. In the following section, we design a distributed load balancing algorithm for setting the load of each cell. Our ultimate goal is to assign the load as close as possible to the optimum load obtained (i.e., the Nash Equilibrium Solutions (NES)).

Appendix B: The placement of the Picocells on the overlay Macrocell network

As shown in Fig. 11 Picocells are arrenged in three circles around the BTS anntena. We refrained from putting any Picocells in the border area of Macrocells. The minimum distance from Macrocell antenna and Picocell antenna is assumed 75 m [28], but we put the Picocells farther than 100 m from the Macrocell to eliminate any interference between them.

Fig. 11

Three layers of Picocells around the BTS antenna

In the first layer, Picocells are arranged on a circle with a radious of 150 m around the center of MBS (see Fig. 12). The number of Picocells in this layer is calculated as follows:

Fig. 12

Distance between first layer Picocells and MBS

In the secound layer, Picocell are arranged on a circle with a radious of 250 m around the center of MBS (see Fig. 13). The number of Picocells in this layer is calculated as follows:

Fig. 13

Distance between second layer Picocells and MBS

Similary, in the third layer, Picocells are arranged on a circle with a radious of 350 m around the center of MBS (see Fig. 14). The number of Picocells in this layer is calculated as follows:

Fig. 14

Distance between third layer Picocells and MBS

In total, we have 42 Picocells around each Macrocell antenna. Consequently, each Macrocell is associated with 14 Picocells.