Abstract
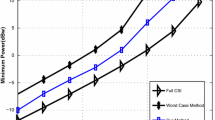
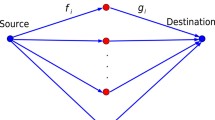
In this paper, a new robust problem is proposed for relay beamforming in relay system with stochastic perturbation on channels of multi user and relay network. The robust problem aims to minimize the transmission power of relay nodes while the imperfect channel information (CSI) injects stochastic channel uncertainties to the parameters of optimization problem. In the power minimization framework, the relays amplification weights and phases are optimized assuming the availability of Gaussian channel distribution. The power sum of all relays is minimized while the outage probability of the instantaneous capacity (or SINR) at each link is above the outage capacity (or SINR) for each user. The robust problem is a nonconvex SDP problem with Rank constraint. Due to the nonconvexity of the original problem, three suboptimal problems are proposed. Simulation and numerical results are presented to compare the performance of the three proposed solutions with the existing worst case robust method.




Similar content being viewed by others
Notes
The function \(\lambda _{max} \left( {\mathbf{X}} \right) \) is non-differentiable when the multiplicity order of maximum eigenvalue is more than one.
References
Sendonaris, A., Erkip, E., & Aazhang, B. (2003). User cooperation diversity. Part I: System description. IEEE Transactions on Communications, 51(11), 1927–1938.
Sendonaris, A., Erkip, E., & Aazhang, B. (2003). User cooperation diversity. Part II: Implementation aspects and performance analysis. IEEE Transactions on Communications, 51(11), 1939–1948.
Laneman, J., Tse, D., & Wornell, G. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50(12), 3062–3080.
Dohler, M., & Li, Y. (2010). Cooperative communication: Hardware, channel and PHY. London: Wiley.
Soleimani-Nasab, E., Kalantari, A., & Ardebilipour, M. (2011). Performance analysis of selective DF relay networks over rician fading channels. In Proceedings of 2011 IEEE Symposium on Computers and Communications (ISCC), pp. 117–122.
Soleimani-Nasab, E., Kalantari, A., & Ardebilipour, M. (2011). Performance analysis of multi-antenna DF relay networks over Nakagami-\(m\) fading channels. IEEE Communications Letters, 15(12), 1372–1374.
Kalantari, A., Soleimani-Nasab, E., & Ardebilipour, M. (2011). Performance analysis of best selection DF relay networks over Nakagami-\(n\) fading channels. In Proceedings of 2011 19th Iranian conference on electrical engineering (ICEE), pp. 1–5.
Kalantari, A., Soleimani-Nasab, E., & Ardebilipour, M. (2012). Performance analysis of multi-antenna relay systems with imperfect channel estimation. In Proceedings of 2012 20th telecommunications forum (TELFOR), pp. 823–826.
Soleimani-Nasab, E., Ardebilipour, M., & Kalantari, A. (2014). Performance analysis of selective combining decode-and-forward relay networks over Nakagami-\(n\) and Nakagami-\(q\) fading channels. To appear, Wireless Communications on Mobile Computer.
Soleimani-Nasab, E., Ardebilipour, M., Kalantari, A., & Mahboobi, B. (2013). Performance analysis of multi-antenna relay networks with imperfect channel estimation. AEU-International Journal of Electronics and Communications, 67(1), 45–57.
Raeisi, A., Mahboobi, B., Zokaei, S., & Ardebilipoor, M. (2011). Optimal power aware routing for decode-and-forward multi-hop relay networks. In Proceedings of 2011 IEEE GCC conference exhibition (GCC), pp. 525–528.
Soleimani-Nasab, E., Kalantari, A., Ardebilipour, M., & Rajabi, O. (2011). Performance analysis of multi-antenna AF two-way relaying over Rayleigh fading channels. In Proceedings of 2011 19th telecommunication forum (TELFOR), pp. 517–519.
Rajabi, O., Kalantari, A., Soleimani-Nasab, E., & Ardebilipour, M. (2011). Uplink and downlink beamforming in two-way relay networks. In Proceedings of 2011 19th telecommunication forum (TELFOR), pp. 373–376.
Soleimani-Nasab, E., & Ardebilipour, M. (2012). On the performance of multi-antenna AF two-way relaying over Nakagami-\(m\) fading channels. In Proceedings of 2012 sixth international symposium telecommunication (IST), pp. 200–204.
Soleimani-Nasab, E., Matthaiou, M., & Ardebilipour, M. (2013). On the performance of multi-antenna AF relaying systems over Nakagami-\(m\) fading channels. In Proceedings of 2013 IEEE international conference communication (ICC), pp. 3041–3046.
Soleimani-Nasab, E., Matthaiou, M., & Karagiannidis, G. (2013). Two-way interference-limited AF relaying with selection-combining. In Proceedings of 2013 IEEE international conference acoustics, speech and signal process (ICASSP), pp. 4992–4996.
Soleimani-Nasab, E., Matthaiou, M., Ardebilipour, M., & Karagiannidis, G. (2013). Two-way AF relaying in the presence of co-channel interference. IEEE Transactions on Communications, 61(8), 3156–3169.
Soleimani-Nasab, E., Matthaiou, M., & Ardebilipour, M. (2013). Multi-relay MIMO systems with OSTBC over Nakagami-\(m\) fading channels. IEEE Transactions on Vehicular Technology, 62(8), 3721–3736.
Soleimani-Nasab, E., & Ardebilipour, M. (2013). Multi-antenna AF two-way relaying over Nakagami-\(m\) fading channels. Wireless Personal Communications, 73(3), 717–729.
Soleimani-Nasab, E., Matthaiou, M., Karagiannidis, G., A., & Ardebilipour, M. (2013). Two-way interference-limited AF relaying over Nakagami-\(m\) fading channels. In Proceedings of 2013 IEEE global communication conference (GLOBECOM), pp. 4380–4386.
Alikhani, E., Mahboobi, B., Ardebilipour, M., Kheyri, H., & Alikhani, S. (2011). Adaptive radio resource allocation with frequency reusing for OFDMA cellular relay networks. In Proceedings of 2011 3rd international conference ubiquitous future networks (ICUFN), pp. 395–400.
Alikhani, E., Mahboobi, B., Ardebilipour, M., & Alikhani, A. (2011). Resource allocation and frequency reusing for multihop relay systems. In Proceedings of 2011 19th Iranian conference electrical engineering (ICEE), pp. 1–6.
Raeisi, A., Mahboobi, B., Zokaei, S., & Ardebilipour, M. (2011). Near-optimal power aware routing for amplify-and-forward multi-hop networks. In Proceedings of 2011 IEEE GCC conference exhibition (GCC), pp. 521–524.
Mahboobi, B., Mohammadi, M., Ardebilipour, M., & Moratab, A. (2010). QoS aware power allocation in multi-hop multi-relay network. In Proceedings of 2010 international congress ultra modern telecommunications control systems workshops (ICUMT), pp. 327–330.
Mohammadi, M., Mahboobi, B., Ardebilipour, M., & Mobini, Z. (2010). Power-optimized multi-hop multi-branch amplify-and-forward cooperative systems. In Proceedings of 2010 5th IEEE international symposium wireless pervasive somputing (ISWPC), pp. 534–539.
Alikhani, E. S., Mahboobi, B., & Ardebilipour, M. (2012). Interference aware resource allocation in orthogonal frequency-division multiple access-based relay networks. IET Communications, 6(11), 1364–1373.
Mohammadi, M., Mobini, Z., Ardebilipour, M., & Mahboobi, B. (2013). Performance analysis of generic amplify-and-forward cooperative networks over asymmetric fading channels. Wireless Personal Communications, 72(1), 49–70.
Havary-Nassab, V., Shahbazpanahi, S., Grami, A., & Luo, Z.-Q. (2008). Distributed beamforming for relay networks based on second-order statistics of the channel state information. IEEE Transactions on Signal Processing, 56(9), 4306–4316.
Jing, Y., & Jafarkhani, H. (2009). Network beamforming using relays with perfect channel information. IEEE Transactions on Information Theory, 55(6), 2499–2517.
Fazeli-Dehkordy, S., Shahbazpanahi, S., & Gazor, S. (2009). Multiple peer-to-peer communications using a network of relays. IEEE Transactions on Signal Processing, 57(8), 3053–3062.
Grant, M., & Boyd, S. (2009). CVX: Matlab software for disciplined convex programming, [Online]. Available: http://stanford.edu/boyd/cvx.
Chalise, B., & Vandendorpe, L. (2009). Joint optimization of multiple MIMO relays for multi-point to multi-point communication in wireless networks. In Proceedings of IEEE workshop signal processing advances in wireless communications (SPAWC), pp. 479–483.
Chae, C.-B., Tang, T., Heath, R., & Cho, S. (2008). MIMO relaying with linear processing for multiuser transmission in fixed relay networks. IEEE Transactions on Signal Processing, 56(2), 727–738.
Zhang, R., Chai, C. C., & Liang, Y.-C. (2009). Joint beamforming and power control for multiantenna relay broadcast channel with QoS constraints. IEEE Transactions on Signal Processing, 57(2), 726–737.
Chalise, B., & Vandendorpe, L. (2010). Optimization of MIMO relays for multipoint-to-multipoint communications: Nonrobust and robust designs. IEEE Transactions on Signal Processing, 58(12), 6355–6368.
Chalise, B., & Vandendorpe, L. (2009). MIMO relay design for multipoint-to-multipoint communications with imperfect channel state information. IEEE Transactions on Signal Processing, 57(7), 2785–2796.
Mahboobi, B., Ardebilipour, M., Kalantari, A., & Soleimani-Nasab, E. (2013). Robust cooperative relay beamforming. IEEEWireless Communications Letters, 2(4), 399–402.
Vucic, N., & Boche, H. (2009). Robust QoS-constrained optimization of downlink multiuser MISO systems. IEEE Transactions on Signal Processing, 57(2), 714–725.
Botros, M., & Davidson, T. (2007). Convex conic formulations of robust downlink precoder designs with quality of service constraints, 1(4), pp. 714–724.
Rong, Y., Vorobyov, S. A., & Gershman, A. B. (2006). Robust linear receivers for multi-access space-time block-coded MIMO systems: A probabilistically constrained approach. IEEE IEEE Journal on Selected Areas in Communications, 24, 1560–1570.
Chung, P.-J., Du, H., & Gondzio, J. (2011). A probabilistic constraint approach for robust transmit beamforming with imperfect channel information. IEEE Transactions on Signal Processing, 59(6), 2773–2782.
Ntranos, V., Sidiropoulos, N., & Tassiulas, L. (2009). On multicast beamforming for minimum outage. IEEE Transactions on Wireless Communications, 8(6), 3172–3181.
Goldsmith, A. (2005). Wireless communications. Cambridge: Cambridge University Press.
Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2000). Handbook of semidefinite programming—theory, algorithms, and applications. Berlin: Springer.
Sturm, J. F. (1999). Using SeDuMi 1.02, a Matlab toolbox for optimization over symmetric cones, vol. 11–12, pp. 625–653.
Boyd, H. S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge University Press.
Karipidis, E., Sidiropoulos, N. D., & Luo, Z. (2008). Quality of service and max-min fair transmit beamforming to multiple cochannel multicast groups. IEEE Transactions on Signal Processing, 56, 1268–1279.
Luo, Z., Sidiropoulos, N. D., Tseng, P., & Zhang, S. (2007). Approximation bounds for quadratic optimization with homogeneous quadratic constraint. SIAM Journal on Optimization, 18, 1–28.
Tsung-Hui, C., Zhi-Quan, L., & Chong-Yung, C. (2008). Approximation bounds for semidefinite relaxation of max-min-fair multicast transmit beamforming problem. IEEE Transactions on Signal Processing, 56, 3932–3943.
Wing-Kin, M., Davidson, T. N., Kon Max, W., Zhi-Quan, L., & Pak-Chung, C. (2002). Quasi-maximum-likelihood multiuser detection using semi-definite relaxation with application to synchronous CDMA. IEEE Transactions on Signal Processing, 50, 912–922.
Nemirovski, A., & Ben-Tal, A. (2001). Lectures on modern convex optimization: Analysis, algorithms, and engineering applications. Society for Industrial Mathematics.
Horn, R., & Johnson, C. (1990). Matrix analysis. Cambridge University Press, Cambridge. [Online]. Available: http://books.google.com/books?id=PlYQN0ypTwEC.
Marks, B. R., & Wright, G. P. (1978). A general inner approximation algorithm for nonconvex mathematical programs. Operations Research, 26(4), 681–683.
Rockafellar, R. T. (1996). Convex analysis. Princeton Mathematical.
Horst, R., Pardalos, P., & Van Thoai, N. (2000). Introduction to global optimization, ser. Nonconvex optimization and its applications. Berlin: Springer.
Apkarian, P., & Tuan, H. D. (1999). Concave programming in control theory. Journal of Global Optimization, 15, 343–370.
Nesterov, Y. E., & Nemirovskii, A. S. (1994). Interior point polynomial algorithms in convex programming. SIAM Studies. Applied Math., vol. 13.
Nesterov, Y. E., & Todd, M. J. (1997). Self-scaled barriers and interior-point methods for convex programming. Mathematics of Operations Research, 22(1), 1–42.
Nesterov, Y. E., & Todd, M. J. (1998). Primal-dual interior-point methods for self-scaled cones. SIAM Journal on Optimization, 8(2), 324–364.
Petersen, K. B., & Pedersen, M. S. (2008). The matrix cookbook.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix I: Proof of (13) and (14)
Proof of (13) and (14) The mean of \(Z_k\) can be written as
Note that, the expectation is taken over fading channel coefficients i.e. \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\). By the above relation (13) is deduced. The variance of \({Z_k}\) is computed as follows
To simplify the above expression, consider the following Lemma.
Lemma 1
If \({\mathbf{X}} \in {R^{m \times n}},{\mathbf{Y}} \in {R^{n \times m}}\), then the following equation holds.
Proof
The proof is easily concluded by using [60]. \(\square \)
Using the above lemma, (59) can be written as
Therefore, the variance of \({Z_k}\) is as follows
Since \(X\) is a positive semi-definite matrix, (62) can be rewritten as
where
Using \(S = {\mathbf{L}}_k^Hvec\left( {\mathbf{X}} \right) \), the variance of \({Z_k}\) is expressed as follows
Some Lemmas
Lemma 2
Let \({\mathbf{A}} = \left( {\begin{array}{cc} {\mathbf{B}}&{}{{{\mathbf{C}}^H}}\\ {\mathbf{C}}&{}{\mathbf{D}} \end{array}} \right) \) be a symmetric matrix with \(k \times k\) block \({\mathbf{B}}\) and \(l \times l\) block \({\mathbf{D}}\). Assume that \({\mathbf{B}}\) is a positive definite matrix. Then \({\mathbf{A}}\) is positive (semi) definite if and only if the matrix \({\mathbf{D}} - {\mathbf{C}}{{\mathbf{B}}^{ - 1}}{{\mathbf{C}}^H}\) is positive (semi) definite (this matrix is called the Schur complement of \({\mathbf{B}}\) in \({\mathbf{A}}\)).
Proof
See [51]. \(\square \)
Lemma 3
Let \(\mathbf {x}\in \mathbb {C}^{m-1}\), \(t \in \mathbb {\mathfrak {R}} \) and \({{\mathbf{I}}_{m - 1}}\) be a \(\left( {m - 1} \right) \times \left( {m - 1} \right) \) identity matrix. Then the cone \({{\mathcal {L}}^m}\), \(m > 1\), is Semi-definite representable, i.e.
Proof
To prove the this lemma, we should note the definition of Lorentz cone which is \(\left( {\begin{array}{c} \mathbf {x}\\ t \end{array}} \right) \in {{\mathcal {L}}^m}\) if and only if \(\left\| \mathbf {x}\right\| _2 \le t\). By choosing \(\mathbf {C}=\mathbf {x}^T\), \(\mathbf {D}=t\) and \(\mathbf {B}=t.\mathbf {I}_m-1\) and using Lemma 2, the proof is completed. \(\square \)
Appendix II
The aim of this appendix is to show that the values of \({{\mu }_{{{\mathbf{Y}}_k}}}\) and \({{\varvec{\Phi }}_k}\) that are used in (13) and (14) can be computed based on first, second and forth order cumulants of \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\). To proceed with the proof of the above claim, the following lemma is needed.
Lemma 4
For \({\mathbf{x}},{\mathbf{y}} \in {R^{m \times 1}}\),
Proof
By defining \({\mathbf{u}} \,{=}\, \left( {{\mathbf{x}} \odot {\mathbf{y}}} \right) {\left( {{\mathbf{x}} \odot {\mathbf{y}}} \right) ^H}\), the \(\left( {i,j} \right) \)th component of \({\mathbf{u}}\) is \({u_{i,j}} \,{=}\, \left( {{x_i}{y_i}} \right) {\left( {{x_j}{y_j}} \right) ^*}\). By rewriting, the \(\left( {i,j} \right) \)th component of \({\mathbf{v}} = {\mathbf{x}}{{\mathbf{x}}^H} \odot {\mathbf{y}}{{\mathbf{y}}^H}\) as \({v_{i,j}} = {x_i}x_j^*.{y_i}y_j^*\), we conclude.
Since \({{\mu }_{{{\mathbf{Y}}_k}}}\) can be written as
It is sufficient to interpret the terms \({{\mu }_{{\mathbf{R}}_h^k}}\), \(\,{{\mu }_{{{\mathbf{Q}}_k}}}\), \({{\mu }_{{{\mathbf{D}}_k}}}\) versus the statistics \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\). Using the fact that \({\left( {X \odot Y} \right) ^H} = X^H \odot {Y^H}\) and using Lemma 4, the first term in the right hand side of (70) can be written as
Since \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\) are independent random vectors
where \({\mathbf {R}_{{f_k}}}\) and \({\mathbf {R}_{{g_k}}}\) can be interpreted versus first and second order cumulants of \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\). obviously we can write
\({{\mu }_{{{\mathbf{D}}_k}}}\) and \({{\mu }_{{{\mathbf{D}}}}}\) can be easily written as
To express \({{\varvec{\Phi }}_k}\) versus cumulants of \({\mathbf {R}_{{f_k}}}\) and \({\mathbf {R}_{{\mathbf{g}_\mathbf{k}}}}\), consider the following definition
where \({{\mathbf{B}}_k} = vec\left( {{\mathbf{R}}_h^k - {\gamma _k}{{\mathbf{Q}}_k} - {\gamma _k}{{\mathbf{D}}_k}} \right) \). By substituting \(\mathbf{R}_\mathbf{h}^\mathbf{k}\), \({\mathbf{Q}_\mathbf{k}}\), and \({{\mathbf{D}}_k}\) in (76), \({{\mathbf{B}}_k}\) can be calculated versus channel coefficients as
\(\square \)
Using the Lemma 4, (77) can be simplified as
By substituting (78) in (76) and expanding it, we get to
where
To compute \({{\varvec{\Phi }}_k}\), each of the nine terms will be computed sequentially versus the statistics of complex symmetric Gaussian vectors \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\).
Using Lemma 4, \({\varvec{\Phi }}_k^1\) can be simplified as
where \({{\mathbf{G}}_k}\) and \({{\mathbf{F}}_k}\) are
The entries of \({{\mathbf{F}}_k}\) and \({{\mathbf{G}}_k}\) are calculated using up to fourth order moments of random components of \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\), respectively. We will show later that all of the terms of \({\varvec{\Phi }}_k^{j}, j=1,2,\ldots ,9\) can be written as functions of \({{\mathbf{F}}_k}\) and \({{\mathbf{G}}_k}\). For the numerical results section, we need to compute \({{\mathbf{F}}_k}\) and \({{\mathbf{G}}_k}\) for normal distribution, hence we calculate these terms in the sequel. Since \({{\mathbf{G}}_k}\) is similar to \({{\mathbf{F}}_k}\), we only compute the closed form value of \({{\mathbf{F}}_k}\). by denoting \({{\hat{\mathbf{f}}}_k}\) and \({\hat{\mathbf{g}}_k}\) respectively as the perturbation vector of \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\) which are i.i.d complex symmetric gaussian vector with zero mean variance \(\sigma _f^2\), we can write
where \({\left( {{{\mathbf{e}}_j}} \right) _{R \times 1}} = {[\underbrace{0,0,\ldots ,0}_{j - 1},1,0,\ldots 0]^T}\) and the second and forth order moment of \(f_{k,j}\), \(j{th}\) element of \(\hat{\mathbf{f}}_k\), are respectively \(m_2^{{f_{k,j}}} = \sigma _{{f_{k,j}}}^2\) and \( m_4^{{f_{k,j}}} = 2{\left( {m_2^{{f_{k,j}}}} \right) ^2} = 2\sigma _{{f_{k,j}}}^4\) . The first two terms of the right hand side of (88) can be computed using the following relations
By writting \({\mathbf{f}}_k\) (and similarly \({\mathbf{g}}_k\)) as the following sum of zero mean random vector and a constant mean vector
we can obtain \(\mathbf {F}_k\) by some algebraic manipulation
The final simplified form of \({{{\mathbf{F}}}_k}\) can be written as
As mentioned earlier, calculation of \({{{\mathbf{G}}}_k}\) resembles that of \({{{\mathbf{F}}}_k}\).
Utilizing Lemma 4, (81) can be written as
where \({{\mathbf{R}}_{{{\mathbf{f}}_{\mathbf{p}}}}} = vec({{\mathbf{f}}_p}{\mathbf{f}}_p^H) = vec({{\mathbf{R}}_{{{{{\hat{\mathbf{f}}}}}_{\mathbf{p}}}}} + {{{\bar{\mathbf{f}}}}_p}{{\bar{\mathbf{f}}}}_p^H)\) consists of up to second order cumulants of \({{\mathbf{f}}_p}\). After that, (82) can be written as
where \({{{{\tilde{\mathbf{g}}}}}_k} = vec\left( {diag\left[ {{{\mathbf{g}}_k}} \right] } \right) = \sum \limits _{j = 1}^R {{g_{k,j}}{{\mathbf{q}}_j}}\) and \({{\mathbf{q}}_j} \mathop {=}\limits ^{\varDelta } vec\left( {diag\left[ {{{\mathbf{e}}_j}} \right] } \right) \). By following the same approach used in the computation of \({\mathbf{F}}_k\) and \({\mathbf{G}}_k\), we can write \({{{\tilde{\mathbf{g}}}}_k}\) as sum of its mean and zero mean random part \({{{\tilde{\mathbf{g}}}}_k} = {{{\hat{\tilde{\mathbf{g}}}}}_k} + {{{\bar{\tilde{\mathbf{g}}}}}_k}\). Therefore we have
for i.i.d complex gaussian symmetric gaussian \({{\mathbf{g}}_k}\), (96) can be further simplified as
where \({\mathbf{R}}_{{{\hat{\tilde{\mathbf{g}}}}}_k}\triangleq E\left[ {{{\hat{\tilde{\mathbf{g}}}}}_k}{{{\hat{\tilde{\mathbf{g}}}}}_k}^H\right] =\sum \limits _{j = 1}^R {\sigma _{g_{k,j}}^2}{\mathbf{q}}_j{\mathbf{q}}_j^T\) .
Using Lemma 4, (83) can be written as
The equation in (84), by using Lemma 4, can be rewritten as
Since \(vec\left( {{\mathbf{x}} \odot {\mathbf{y}}} \right) = vec\left( {\mathbf{x}} \right) \odot vec\left( {\mathbf{y}} \right) \), (99) can be written as
Again, by using lemma 4, the above expression can be rewritten as
To compute \({\varvec{\Phi }}_k^8\), we used the fact that \(vec\left( {{\mathbf{x}} \odot {\mathbf{y}}} \right) = vec\left( {\mathbf{x}} \right) \odot vec\left( {\mathbf{y}} \right) \) as follows
Again, by using Lemma 4, the above expression can be rewrite as
From the above, it is obvious that the entries of \({\varvec{\Phi }}_k^6\), \({\varvec{\Phi }}_k^7\), \({\varvec{\Phi }}_k^8\) and \({\varvec{\Phi }}_k^9\) consist of up to second and fourth order cumulants of \({{\mathbf{f}}_k}\) and \({{\mathbf{g}}_k}\), respectively. Finally, the expression of (79) can be computed based on \({\mathbf{R}}_f^k\), \({{\mathbf{G}}_k}\) and \({{\mathbf{F}}_k}\).
Rights and permissions
About this article
Cite this article
Mahboobi, B., Soleimani-Nasab, E. & Ardebilipour, M. Outage Probability Based Robust Distributed Beam-Forming in Multi-User Cooperative Networks with Imperfect CSI. Wireless Pers Commun 77, 1629–1658 (2014). https://doi.org/10.1007/s11277-013-1520-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-013-1520-2