Coverage Self-Optimization for Randomly Deployed Femtocell Networks

Abstract

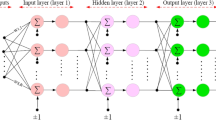
There is an ever increasing demand on wireless communication systems for improved indoor coverage, greater capacity and enhanced user services. Energy efficient, small scale femtocell networks deployed in home, office and other indoor environments are one of the promising means of satisfying these demands. They can provide substantial benefits to both operators and users, such as a reduction in capital expenditures and operational expenditures, easy plug-and-play and optimized indoor coverage. Because of the random deployment behavior by the users, femtocell base stations (FBSs) should have cognitive position awareness, automatic parameter tuning and learning abilities. This will allow for self-optimization of the indoor coverage with the minimal interference to outdoor users. This paper first proves that the optimal coverage radii for FBS exist in typical indoor environments with position awareness enabled technology. Then, a dynamic power allocation technique for FBS is designed and analyzed in this paper by considering the path loss and different wall penetration conditions. To further enable the intelligent coverage self-optimization for randomly deployed indoor FBSs, a novel joint dynamic power allocation and antenna pattern selection scheme using the artificial neural network is proposed. Performance results are presented to illustrate the effectiveness and accuracy of the proposed coverage technique for randomly deployed femtocell networks.

Appendix

1.1 Lemma 1

When $0 < R_f \le D_s /2$, $\delta$ is a decreasing function of $R_f$ because

$$\begin{aligned} \frac{{d\delta _1 }}{{dR_f }} = \frac{{ - 2\pi R_f }}{{D_s^2 }} < 0. \end{aligned}$$

(50)

Thus, the minimum value of $\delta$ is given by $\delta _1^{\min } = \delta _1 (D_s /2) = 1 - \pi /4 = 0.21$ when $R_f = D_s /2$. For $D_s /2 < R_f < \sqrt{2} D_s /2$, define $\alpha = \arccos [D_s /(2R_f )],0 < \alpha < \pi /4$ and substitute $D_s = 2R_f \cos \alpha$ into (8). After some manipulation, we obtain

$$\begin{aligned} \delta _2 = \left( {2\alpha - \pi /4} \right) \tan ^2 \alpha - 2\tan \alpha + \left( {1 + 2\alpha - \pi /4} \right) . \end{aligned}$$

(51)

From

$$\begin{aligned} \because \frac{{d\delta _2 }}{{d\alpha }} = 4\left( \alpha - \frac{\pi }{8}\right) \tan \alpha (1 + \tan ^2 \alpha ) = 0 \therefore \alpha = \frac{\pi }{8}, \end{aligned}$$

(52)

and

$$\begin{aligned}&\because \frac{{d^2 \delta _2 }}{{d\alpha ^2 }} = 4\left( \alpha - \frac{\pi }{8}\right) + 4\tan \alpha + 16\left( \alpha - \frac{\pi }{8}\right) \tan ^2 \alpha + 4\tan ^3 \alpha + 12\left( \alpha - \frac{\pi }{8}\right) \tan ^4 \alpha \nonumber \\&\therefore \frac{{d^2 \delta _2 }}{{d\alpha ^2 }}\left| {_{\alpha = \frac{\pi }{8}} } \right. = 4\tan \alpha + 4\tan ^3 \alpha = 1.94 > 0, \end{aligned}$$

(53)

the minimum value of $\delta _2$ is given by $\delta _2^{\min } \left| {_{\alpha = \pi /8} } \right. = 1 - 2\tan \alpha = 0.17$ with $\alpha = \pi /8 = 0.393$ and $D_s = 2R_f \cos \alpha = 1.85R_f$. When $R_f \ge \sqrt{2} D_s /2$, $\delta$ is an increasing function of $R_f$ according to

$$\begin{aligned} \frac{{d\delta _3 }}{{dR_f }} = \frac{{2\pi R_f }}{{D_s^2 }}\; > 0. \end{aligned}$$

(54)

Thus, the minimum value of $\delta$ is given by $\delta _3^{\min } = \delta _3 (\sqrt{2} D_s /2) = \pi /2 - 1 = 0.57$, with $R_f = \sqrt{2} D_s /2$. The minimum value of $\delta$ is then $\delta ^{\min } = \min (\delta _1^{\min } ,\delta _2^{\min }, \delta _3^{\min } ) = \delta _2^{\min } = 0.17$ with an optimal FBS coverage radius of $R_f^{Opt} = \arg \min \delta = 0.54D_s$.

1.2 Lemma 2

When $0 < R_f \le D_s$, $\delta$ is a decreasing function of $R_f$ because

$$\begin{aligned} \frac{{d\delta _1 }}{{dR_f }} = \frac{{ - \pi R_f }}{{2D_s^2 }}\; <0. \end{aligned}$$

(55)

Thus, the minimum value of $\delta$ is given by $\delta _1^{\min } = \delta _1 (D_s ) = 1 - \pi /4 = 0.21$ when $R_f = D_s$.

For $D_s < R_f < \sqrt{2} D_s$, define $\alpha = \arccos [D_s/(R_f )], 0 < \alpha < \pi /4$ and substitute $D_s=R_f\cos \alpha$ into (15). After some manipulation, we obtain

$$\begin{aligned} \delta _2 = \left( {2\alpha - \pi /4} \right) \tan ^2 \alpha - 2\tan \alpha + \left( {1 + 2\alpha - \pi /4} \right) . \end{aligned}$$

(56)

Based on the results in (52) and (53), the minimum value of $\delta _2$ is given by $\delta _2^{\min } \left| {_{\alpha = \pi /8} } \right. = 1 - 2\tan \alpha = 0.17$ when $\alpha = \pi /8 = 0.393$ and $D_s=R_f\cos \alpha =0.92R_f$. When $R_f \ge \sqrt{2} D_s$, $\delta$ is an increasing function of $R_f$ according to

$$\begin{aligned} \frac{{d\delta _3 }}{{dR_f }} = \frac{{\pi R_f }}{{2D_s^2 }}\; > 0. \end{aligned}$$

(57)

Thus, the minimum value of $\delta$ is given by $\delta _3^{\min } = \delta _3 (\sqrt{2} D_s ) = \pi /2 - 1 = 0.57$ when $R_f = \sqrt{2} D_s$. The minimum $\delta$ is then $\delta ^{\min } = \min (\delta _1^{\min } ,\delta _2^{\min } ,\delta _3^{\min } ) = \delta _2^{\min } = 0.17$ with an optimal FBS coverage radius of $R_f^{Opt} = \arg \min \delta = 1.08D_s$.

1.3 Lemma 3

When $0 < R_f \le D_s /2$, $\delta$ is a decreasing function of $R_f$ according to

$$\begin{aligned} \frac{{d\delta _1 }}{{dR_f }} = \frac{{ - \pi R_f }}{{D_s^2 }}\; < 0. \end{aligned}$$

(58)

Thus, the minimum value of $\delta$ is given by $\delta _1^{\min } = \delta _1 (D_s /2) = 1 - \pi /8 = 0.61$ when $R_f = D_s /2$. When $D_s /2 < R_f < D_s$, define $\alpha = \arccos [D_s /(2R_f )],0 < \alpha < \pi /3$ and substitute $D_s=2R_f\cos \alpha$ into (24). After some manipulation, $\delta _2$ is given by

$$\begin{aligned} \delta _2&= \frac{1}{{D_s^2 }} \left( {D_s^2 - \frac{{D_s }}{2}\sqrt{4R_f^2 - D_s^2 } - 2D_s \sqrt{R_f^2 - D_s^2 } - \frac{\pi }{2}R_f^2 + 2\alpha R_f^2 + 2\mu R_f^2 } \right) \nonumber \\&= \left( {\frac{\alpha }{2} - \frac{\pi }{8}} \right) \tan ^2 \alpha - \frac{1}{2}\tan \alpha + \left( {1 + \frac{\alpha }{2} - \frac{\pi }{8}} \right) . \end{aligned}$$

(59)

Based on

$$\begin{aligned} \because \frac{{d\delta _2 }}{{d\alpha }} = \left( \alpha - \frac{\pi }{4}\right) \tan \alpha (1 + \tan ^2 \alpha )= 0, \; \therefore \alpha = \frac{\pi }{4} \end{aligned}$$

(60)

and

$$\begin{aligned}&\because \frac{{d^2 \delta _2 }}{{d\alpha ^2 }} = \left( \alpha - \frac{\pi }{4}\right) + \tan \alpha + 4\left( \alpha - \frac{\pi }{4}\right) \tan ^2 \alpha + \tan ^3 \alpha + 3\left( \alpha - \frac{\pi }{4}\right) \tan ^4 \alpha \nonumber \\&\therefore \frac{{d^2 \delta _2 }}{{d\alpha ^2 }}\left| {_{\alpha = \frac{\pi }{4}} } \right. = \tan \alpha + \tan ^3 \alpha = 2 > 0. \end{aligned}$$

(61)

The minimum value of $\delta _2$ is given by $\delta _2^{\min } \left| {_{\alpha = \pi /4} } \right. = 1 - 0.5\tan \alpha = 0.5$ when $\alpha = \pi /4 = 0.79$ and $D_s = 2R_f \cos \alpha = 1.41R_f$. When $D_s \le R_f < \sqrt{5} D_s /2$, define $\alpha = \arccos (D_s/R_f), \beta = \arctan (1/2) - \alpha , \mu = \arccos [D_s/(2R_f)], \gamma = \arctan (2) - \mu , 0 \le \alpha < \arctan (1/2), \pi /3 \le \mu < \arctan (2)$ and substitute $D_s = R_f \cos \alpha = 2R_f \cos \mu , \mu = \arccos [(\cos \alpha )/2]$ into (24). After some manipulation, we obtain

$$\begin{aligned} \delta _3&= 1 - \frac{1}{2}\tan \mu - 2\tan \alpha + \left( {2\alpha + 2\mu - \frac{\pi }{2}} \right) \sec ^2 \alpha \nonumber \\&= 1 - \frac{{\sqrt{4 - \cos ^2 \alpha } }}{{2\cos \alpha }} - 2\tan \alpha + \left[ {2\alpha + 2\arccos \left( {\frac{1}{2}\cos \alpha } \right) - \frac{\pi }{2}} \right] \sec ^2 \alpha . \end{aligned}$$

(62)

Using $\zeta = \sqrt{4 -\cos ^2 \alpha } /(2\cos \alpha ), \xi = 2\alpha + 2\arccos \left[ {(\cos \alpha )/2} \right] - \pi /2$, (62) can be simplified to

$$\begin{aligned} \delta _3 = (1 - \zeta ) - 2\tan \alpha + \xi \sec ^2 \alpha . \end{aligned}$$

(63)

Based on

$$\begin{aligned} \because \frac{{d\zeta }}{{d\alpha }}&= \frac{{2\sin \alpha \sec ^2 \alpha }}{{\sqrt{4 - \cos ^2 \alpha } }}\frac{{d\xi }}{{d\alpha }} = \sec ^2 \alpha \left( {2 + \frac{{\sin \alpha }}{{\sqrt{4 - \cos ^2 \alpha } }} + 2\xi \tan \alpha } \right) \nonumber \\ \therefore \frac{{d\delta _3 }}{{d\alpha }}&= - \frac{{d\zeta }}{{d\alpha }} - 2\sec ^2 \alpha + \frac{{d\xi }}{{d\alpha }}\sec ^2 \alpha + 2\xi \tan \alpha \sec ^2 \alpha \nonumber \\&= 2\xi \tan \alpha \sec ^2 \alpha = 4 \left[ {\alpha + \arccos \left( {\frac{1}{2}\cos \alpha } \right) - \frac{\pi }{4}} \right] \tan \alpha \sec ^2 \alpha \end{aligned}$$

(64)

and

$$\begin{aligned}&\because 0 \le \alpha < \arctan (1/2),2/\sqrt{5} < \cos \alpha \le 1 \nonumber \\&\therefore \frac{\pi }{3} \le \arccos \left( {\frac{1}{2}\cos \alpha } \right) < \arccos \left( {\frac{1}{{\sqrt{5} }}} \right) \nonumber \\&\therefore \alpha + \arccos \left( {\frac{1}{2}\cos \alpha } \right) \ge \frac{\pi }{3} > \frac{\pi }{4}\nonumber \\&\therefore \frac{{d\delta _3 }}{{d\alpha }} = 4\left[ {\alpha + \arccos \left( {\frac{1}{2}\cos \alpha } \right) - \frac{\pi }{4}} \right] \tan \alpha \sec ^2 \alpha > 0. \end{aligned}$$

(65)

Thus $\delta _3$ is an increasing function of $R_f$ with minimum value $\delta _3^{\min } \left| {_{\alpha = 0,\mu = \pi /3} } \right. = 1 - \sqrt{3} /2 + \pi /6 = 0.66$ when $\alpha =0$, $\mu = \pi /3$ and $D_s=R_f$.

When $R_f \ge \sqrt{5} D_s /2$, $\delta$ is an increasing function of $R_f$ according to

$$\begin{aligned} \frac{{d\delta _4 }}{{dR_f }} = \frac{{\pi R_f }}{{D_s^2 }}\; > 0. \end{aligned}$$

(66)

Thus, the minimum value of $\delta$ is given by $\delta _4^{\min } = \delta _4 (\sqrt{5} D_s /2) = 5\pi /8 - 1 = 0.96$ when $R_f = \sqrt{5} D_s /2$. The minimum value of $\delta$ is then $\delta ^{\min } = \min (\delta _1^{\min } ,\delta _2^{\min } ,\delta _3^{\min } ,\delta _4^{\min } ) = \delta _2^{\min } = 0.5$ with an optimal FBS coverage radius of $R_f^{Opt} = \arg \min \delta = 0.71D_s$.