Performance of Random Access Markov Modelling for Two-Way Buffer-Aided Relaying Networks with Wireless Assisted Links

Abstract

In this paper, we consider two-way relaying networks (TWRNs) in which information of two users randomly exchange via buffer-aided relay. We assume that all nodes work on half-duplex decode-and-forward for relaying of data packets. The relay is equipped with two finite-size buffers and both the users know the exact number of data packets. The data packets are scheduling with different channel access probabilities to avoid collision at relay. The protocols are developed on the basis of selective transmission scheme with states of Markov chain at relay for buffer state information (BSI) and Hybrid buffer state information/channel state information (BSI/CSI). On the basis of these protocols, we investigate closed-from expressions of maximum achievable sum throughput and end-to-end throughput for TWRNs. The numerical results are obtained with the help of CVX software package. Our proposed scheme significantly outperforms the existing two-way buffer-aided relaying scheme in literature.

Appendices

Appendix 1

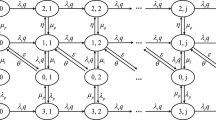
In this appendix, we compute the outage probability discussed in Sect. 3.1. The probability of events $Pr\left( {{\mathcal{S}}_{1} } \right)$ to $Pr\left( {{\mathcal{S}}_{6} } \right)$ can be expressed as,

$$\begin{aligned} & Pr\left( {{\mathcal{S}}_{1} } \right) = Pr\left( {\gamma_{1} \ge \gamma_{0} } \right); \\ & Pr\left( {{\mathcal{S}}_{2} } \right) = Pr\left( {\gamma_{2} \ge \gamma_{0} } \right) \\ & Pr\left( {{\mathcal{S}}_{3} } \right) = Pr\left( {\left( {\gamma_{1} + \gamma_{2} } \right) \ge \gamma_{0}^{sum} } \right) \\ & Pr\left( {{\mathcal{S}}_{4} } \right) = Pr\left( {\gamma_{1} \ge \gamma_{0} } \right); \\ & Pr\left( {{\mathcal{S}}_{5} } \right) = Pr\left( {\gamma_{2} \ge \gamma_{0} } \right) \\ & Pr\left( {{\mathcal{S}}_{6} } \right) = Pr\left( {\gamma_{1} \ge \gamma_{0} , \gamma_{2} \ge \gamma_{0} } \right); \\ \end{aligned}$$

(28)

For Rayleigh fading, probability density functions (pdfs) of instantaneous SNRs $\gamma_{1} \left( i \right)$ and $\gamma_{2} \left( i \right)$ are defined [14] as $f_{{\gamma_{1} }} \left( {\gamma_{1} } \right) = \frac{1}{{\Omega _{1} \gamma }}exp\left( { - \gamma_{1} /\left( {\Omega _{1} \gamma } \right)} \right)$ and $f_{{\gamma_{2} }} \left( {\gamma_{2} } \right) = \frac{1}{{\Omega _{2} \gamma }}exp\left( { - \gamma_{2} /\left( {\Omega _{2} \gamma } \right)} \right)$. We draw the lines using (28) as shown in Fig. 7. The joint pdf is defined in [24] as $f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right) = f_{{\gamma_{1} }} \left( {\gamma_{1} } \right) f_{{\gamma_{2} }} \left( {\gamma_{2} } \right)$ for non-outage regions $\left\{ {Z_{{\gamma_{1} }} , Z_{{\gamma_{2} }} } \right\}$. The outage probability of $u_{1} - r$ link is defined as,

$${\mathcal{P}}_{1r} = 1 - Pr\left( {\gamma_{1} \ge \gamma_{0} } \right) = 1 - \mathop \smallint \limits_{{\gamma_{1} = \gamma_{0} }}^{\infty } f_{{\gamma_{1} }} \left( {\gamma_{1} } \right)d\gamma_{1} = 1 - exp \left( { - \frac{{\gamma_{0} }}{{\Omega _{1} \gamma }}} \right) .$$

(29)

Fig. 7

Instantaneous SNR regions of non-outage events for transmission scheme

We assume that $u_{1} - r$ channel is reciprocal to $r - u_{1}$ channel i.e., ${\mathcal{P}}_{1r} = {\mathcal{P}}_{r1}$. Similarly, we obtain outage probability of $u_{2} - r$ link, ${\mathcal{P}}_{2r}$ discussed in (2). Again, we assume that $u_{2} - r$ channel is reciprocal to $r - u_{2}$ channel i.e., ${\mathcal{P}}_{2r} = {\mathcal{P}}_{r2}$.

For multi-access channel, probability of successful transmission of both users is shown in Fig. 7 by non-outage region $\Delta _{1}$.Thus, outage probability of multiple access channel, ${\mathcal{P}}_{MA} = 1 - Pr\left( {\left( {\gamma_{1} + \gamma_{2} } \right) \ge \gamma_{0}^{sum} } \right)$ in TWRNs is defined as,

$${\mathcal{P}}_{MA} = 1 - \mathop \smallint \limits_{{\gamma_{1} = \gamma_{0} }}^{{\gamma_{0}^{sum} - \gamma_{0} }} \mathop \smallint \limits_{{\gamma_{2} = \gamma_{0}^{sum} - \gamma_{1} }}^{\infty } f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right)d\gamma_{1} d\gamma_{2} - \mathop \smallint \limits_{{\gamma_{2} = \gamma_{0} }}^{\infty } \mathop \smallint \limits_{{\gamma_{1} = \gamma_{0}^{sum} - \gamma_{0} }}^{\infty } f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right)d\gamma_{1} d\gamma_{2}$$

(30)

By substituting value of joint pdfs $f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right)$ in (30), we obtain (3). The outage probability of broadcast channel in TWRNs is defined as,

$${\mathcal{P}}_{BC} = 1 - Pr\left( {\gamma_{1} \ge \gamma_{0} , \gamma_{2} \ge \gamma_{0} } \right) = 1 - \mathop \smallint \limits_{{\gamma_{1} = \gamma_{0} }}^{\infty } \mathop \smallint \limits_{{\gamma_{2} = \gamma_{0} }}^{\infty } f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right)d\gamma_{1} \gamma_{2}$$

(31)

Considering (31) and substituting the value of joint pdfs $f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right)$, we obtain (4). We investigate non-outage events ${\mathcal{S}}_{12}$ and ${\mathcal{S}}_{21}$ which are responsible for successfully deliver of data packers from user 1-to-user 2 and from user 2-to-user 1 respectively and these are expressed as,

$${\mathcal{S}}_{12} = \left( {\left( {{\mathcal{S}}_{1} \cap \overline{{{\mathcal{S}}_{2} }} } \right) \cup \left( {\overline{{{\mathcal{S}}_{4} }} \cap {\mathcal{S}}_{5} } \right)} \right) \cup \left( {{\mathcal{S}}_{1} \cap {\mathcal{S}}_{2} \cap \overline{{{\mathcal{S}}_{3} }} \cap {\mathcal{S}}_{6} } \right) \cup \left( {{\mathcal{S}}_{1} \cap {\mathcal{S}}_{2} \cap {\mathcal{S}}_{3} \cap {\mathcal{S}}_{6} } \right)$$

(32a)

$${\mathcal{S}}_{21} = \left( {\left( {{\mathcal{S}}_{2} \cap \overline{{{\mathcal{S}}_{1} }} } \right) \cup \left( {{\mathcal{S}}_{4} \cap \overline{{{\mathcal{S}}_{5} }} } \right)} \right) \cup \left( {{\mathcal{S}}_{1} \cap {\mathcal{S}}_{2} \cap \overline{{{\mathcal{S}}_{3} }} \cap {\mathcal{S}}_{6} } \right) \cup \left( {{\mathcal{S}}_{1} \cap {\mathcal{S}}_{2} \cap {\mathcal{S}}_{3} \cap {\mathcal{S}}_{6} } \right)$$

(32b)

Considering (32a), outage probability of TWRNs from user 1-to-user 2 is formulated as,

$${\mathcal{P}}_{12}^{out} = 1 - Pr\left( {{\mathcal{S}}_{12} } \right) = 1 - \mathop {\iint }\limits_{{\Delta _{1,lo} ;\Delta _{2,lo} ;\Delta _{3,lo} ;\Delta _{4,lo} }}^{{\Delta _{1,up} ;\Delta _{2,up} ;\Delta _{3,up} ;\Delta _{4,up} }} f_{{\gamma_{1} \gamma_{2} }} \left( {\gamma_{1} , \gamma_{2} } \right)d\gamma_{1} \gamma_{2}$$

(33)

In (33), the integration expression indicates that the summation of integration is computed over the lower limits and upper limits of sets, $\left\{ { \Delta_{1,lo} , \Delta_{1,up} } \right\}$, $\left\{ {\Delta_{2,lo} , \Delta_{2,up} } \right\}$, $\left\{ { \Delta_{3,lo} , \Delta_{3,up} } \right\}$ and $\left\{ { \Delta _{4,lo} ,\Delta _{4,up} } \right\}$ of regions $\Delta _{1}$, $\Delta _{2}$, $\Delta _{3}$, and $\Delta _{4}$. By evaluating (33), we obtain (5). From Fig. 7, it is clear that the non-outage region of event ${\mathcal{S}}_{21}$ is identical to non-outage region of event ${\mathcal{S}}_{21}$. Thus, outage probability from user 1-to-user 2 is equal to outage probability from user 2-to-user 1 i.e., ${\mathcal{P}}_{12}^{out} = {\mathcal{P}}_{21}^{out}$.

Appendix 2

Using (6a) and (8a) we can write,

$${{\mathcal{V}}}_{{n}}{\alpha}_{{n}} = {{\mathcal{V}}}_{0} { K}^{{n}} {{\mathcal{X}}}_{{n}}$$

(34)

where ${{\mathcal{X}}}_{{n}} = \prod \nolimits_{{{i} = {{1}}}}^{{n}} \frac{{{\alpha}_{{i}} }}{{\overline{{{\alpha}_{{i}} }} }}$ and it can be rearranged as ${{\mathcal{X}}}_{{n}} = \frac{{{\alpha}_{{n}} }}{{\overline{{{\alpha}_{{n}} }} }}{{\mathcal{X}}}_{{{n} - {\mathbf{1}}}}$.Thus, $\alpha_{{n}}$ can be written in term of ${{\mathcal{X}}}_{{n}}$ as ${\alpha}_{{n}} = \frac{{{{\mathcal{X}}}_{{n}} }}{{{{\mathcal{X}}}_{{n}} + {{\mathcal{X}}}_{{{n} - {{1}}}} }}$. Substituting ${\alpha}_{{n}}$ in (34), we obtain steady-state probability as,

$${\mathcal{V}}_{n} = {\mathcal{V}}_{0} K^{n} \left( {{\mathcal{X}}_{n} + {\mathcal{X}}_{n - 1} } \right)$$

(35)

Since, we have $\mathop \sum \nolimits_{{{n} = {{0}}}}^{{N}} {{\mathcal{V}}}_{{n}} = {{1}}$. Considering (35), we can write initial steady-state term as,

$${\mathcal{V}}_{0} = \frac{1}{{1 + \mathop \sum \nolimits_{n = 1}^{N} K^{n} \left( {{\mathcal{X}}_{n} + {\mathcal{X}}_{n - 1} } \right)}}$$

(36)

Substituting (34) and (36) in (11), we obtain (13a). Similarly, we can write (13b) for relaying of buffer $B_{2}$ at relay. We consider ${\mathcal{X}}_{0} = 1$ then denominator of (13a) can be expressed as,

$$1 + \mathop \sum \limits_{n = 1}^{N} K^{n} \left( {{\mathcal{X}}_{n} + {\mathcal{X}}_{n - 1} } \right) = \left( {1 + K} \right)\left[ {1 + \mathop \sum \limits_{n = 1}^{N - 1} K^{n} {\mathcal{X}}_{n} + \frac{{K^{N} {\mathcal{X}}_{N} }}{1 + K}} \right]$$

(37)

Substituting (37) in (13a), we can write

$${\mathcal{R}}_{12}^{B} = \frac{{{\mathcal{R}}_{0} \left( { \overline{{{\mathcal{P}}_{1r} }} + \overline{{{\mathcal{P}}_{MA} }} } \right)\left( {1 + \mathop \sum \nolimits_{n = 1}^{N - 1} K^{n} {\mathcal{X}}_{n} } \right)}}{{\left( {1 + K} \right)\left[ {1 + \mathop \sum \nolimits_{n = 1}^{N - 1} K^{n} {\mathcal{X}}_{n} + \frac{{K^{N} {\mathcal{X}}_{N} }}{1 + K}} \right]}}$$

(38)

If birth–death MC is at $N$ state, the buffer $B_{1}$ at relay drops data packets i.e., overflow condition. In this scenario, $u_{1}$ transmits with probability, $\alpha_{N} = 0$. Thus, ${\mathcal{X}}_{N} = 0$ and then (38) can be written as,

$${\mathcal{R}}_{12}^{B} = \frac{{{\mathcal{R}}_{0} \left( { \overline{{{\mathcal{P}}_{1r} }} + \overline{{{\mathcal{P}}_{MA} }} } \right)}}{{\left( {1 + K} \right)}}$$

(39)

Substituting the value of $K$ in (39), we obtain (15a). Similarly, we can obtain ${\mathcal{R}}_{21}^{B}$ for TWRNs that has been expressed in (15b).

Appendix 3

With consideration of (22) and (23), we can express the sum throughput of TWRNs as,

$${\mathcal{R}}_{sum}^{HB/C} = {\mathcal{R}}_{0} \left[ {k_{1} + l_{1} + \left( {\Lambda _{12} +\Lambda _{21} } \right)} \right]$$

(40)

From (40), we observe that the sum throughput should be maximized by maximizing the term $\left( {\Lambda _{12} +\Lambda _{21} } \right)$. In our problem, the set of variable $\left\{ \phi \right\}_{n = 1}^{N}$ is used to express the term $\Lambda _{12}$ while the set of variables $\left\{ \psi \right\}_{m = 1}^{M}$ is used to express the term $\Lambda _{21}$. Both terms $\Lambda _{12}$ and $\Lambda _{21}$ are independent from each other. Thus, sum throughput is maximized individually with maximization of $\Lambda _{12}$ and $\Lambda _{21}$. For maximization of $\Lambda _{12}$, we consider global balance condition and is expressed as,

$${\mathcal{V}}_{n - 1} a_{n - 1} = {\mathcal{V}}_{n} b_{n}$$

(41)

Substituting (8a), (17a) and (21a) in (41), we yield an expression as,

$$\frac{{\phi_{n} }}{{\phi_{n - 1} }} = \frac{{a_{n - 1} }}{{b_{n} }} = \frac{{\overline{{{\mathcal{P}}_{1r} }} \left( {{\mathcal{P}}_{2r} + \overline{{{\mathcal{P}}_{r2} }} \xi_{n - 1} } \right) + \overline{{{\mathcal{P}}_{MA} }} \left( {{\mathcal{P}}_{BC} + \overline{{{\mathcal{P}}_{BC} }} \xi_{n - 1} } \right)}}{{\overline{{{\mathcal{P}}_{r2} }} \left( {{\mathcal{P}}_{1r} + \overline{{{\mathcal{P}}_{1r} }} \overline{{\xi_{n} }} } \right) + \overline{{{\mathcal{P}}_{BC} }} \left( {{\mathcal{P}}_{MA} + \overline{{{\mathcal{P}}_{MA} }} \overline{{\xi_{n} }} } \right)}}$$

(42)

We rearrange the terms in (42) and it can be written as,

$$\xi_{n} \phi_{n} = e\phi_{n} - f\phi_{n - 1} - \xi_{n - 1} \phi_{n - 1}$$

(43)

The coefficients $e$ and $f$ are conferred in (25). By setting $\xi_{0} = 1$ and $\phi_{0} = 1$ and summing both sides of (43) from $n = 1$ to (N − 1), we get

$$\mathop \sum \limits_{n = 1}^{N - 1} \xi_{n} \phi_{n} = \left\{ {\begin{array}{*{20}l} {e\phi_{N - 1} - f\phi_{N - 2} + \cdots - f\phi_{1} ;\; for\; N = odd} \hfill \\ {e\phi_{N - 1} - f\phi_{N - 2} + \cdots + e\phi_{1} - h;\;for\; N = even} \hfill \\ \end{array} } \right.$$

(44)

Considering (43), we can write $\left\{ {\xi_{n} } \right\}_{n = 1}^{N}$ as,

$$\xi_{n} = \frac{{e\phi_{n} + \mathop \sum \nolimits_{k = 1}^{n - 1} \left( { - 1} \right)^{n - k} \left( {e + f} \right)\phi_{k} + \left( { - 1} \right)^{n} h}}{{\phi_{n} }}$$

(45)

Substituting (44) in (22) of $\varLambda_{12}$, we obtain objective function in linear-fractional program (26) which is shown in vector form. The constraints are obtained from basic assumption, range of transmit channel access probability, and overflow condition of $B_{1}$ by considering vector form of (45). We follow similar mathematical operation discussed in (26) to obtain the expression of (27). Combining (26) and (27), we obtain sum throughput in form of linear-fractional program discussed in (24).