Modeling and Analyzing of Millimeter Wave Heterogeneous Cellular Networks by Poisson Hole Process

Abstract

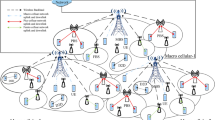
In this paper, a novel Poisson hole process (PHP) modeling of wireless networks is proposed. Contrary to the prior PHP models with circular-shaped holes, we utilized circular sector holes in a random direction to capture the spatial separation between tiers in a millimeter wave (mmWave) heterogeneous cellular network (HCN). In this case, small cell base stations and macrocell base stations are distributed as a PHP and Poisson point process (PPP). Using tools from stochastic geometry, we derive approximate analytical expressions by regarding the effect of one or several holes on coverage probability. Simulation results reveal that compared to conventional PPP-modeling of HCNs, the proposed approaches can provide about 2–3 dB more accurate analysis in terms of signal-to-interference-and-noise ratio coverage probability. Moreover, some interesting insights about the effect of holes on coverage probability and the relation between proposed hole configuration and prior models with circular holes is discovered. It turns out that the analysis based on the proposed PHP model can provide a more general study than prior works.

Appendix

1.1 1. Proof of Lemma 2

Based on the considered cell association rule, the typical UE is associated with a $s\in \{LOS,NLOS\}$ BS in $k{\mathrm{th}}$ tier if the following is satisfied

$$\begin{aligned} P_{k}G_{k}r_{k}^{-\alpha ^{s}}> & {} P_{j}G_{j}r_{j}^{-\alpha ^{s^{\prime }}} \overset{a}{=} P_{k}M_{k}M_{UE}r_{k}^{-\alpha ^{s}}> P_{j}M_{j}M_{UE}r_{j}^{-\alpha ^{s^{\prime }}}\nonumber \\= & {} P_{k}M_{k}r_{k}^{-\alpha ^{s}}> P_{j}M_{j}r_{j}^{-\alpha ^{s^{\prime }}} = r_{j}>(\frac{P_{j}}{P_{k}}\times \frac{M_{j}}{M_{k}})^{1/\alpha ^{s^{\prime }}}\times r_{k}^{\alpha ^{s}/\alpha ^{s^{\prime }}} \end{aligned}$$

(20)

where (a) follows by the serving link directivity gain assumption and $j=1,2$, $s^{\prime }\in \{LOS,NLOS\}$.

Let us denote the serving tier and LOS or NLOS state of BSs by T and S, respectively. The typical UE is associated with a $s\in \{LOS,NLOS\}$ BS in $k{\mathrm{th}}$ tier if and only if it has a $s\in \{LOS,NLOS\}$ BS in that tier, and its nearest BS in $k{\mathrm{th}}$ tier has smaller average power than that of the nearest $s^{\prime }\ne s$ BS in $k{\mathrm{th}}$ tier and the nearest $s^{\prime }\in \{LOS,NLOS\}$ BS in $j\ne k$ tier. Hence, it follows that

$$\begin{aligned}&Pr(T=k,S=s|r_{k}=x)\nonumber \\&\quad =Pr(r_{k}>x^{\alpha ^{s}/\alpha ^{s^{\prime }}} , s^{\prime } \ne s) Pr(r_{j}>R_{j}^{s^{\prime }}(x), j \ne k , s^{\prime } \in {\{LOS,NLOS\}} )\nonumber \\&\quad = exp(-\varLambda _{k,PHP}^{s^{\prime }}([0,x^{\alpha ^{s}/\alpha ^{s^{\prime }}}))) exp\left( - \sum _{s^{\prime }\in \{LOS,NLOS\}} \varLambda ^{s^{\prime }}_{j,PHP}([0,R_{j}^{s^{\prime }}(x) ))\right) \end{aligned}$$

(21)

Note that we approximate PHP distribution of SBSs as PPP with $\lambda _{PHP}$. Therefore, $A_{k}^{s}$ can be expressed as

$$\begin{aligned} A_{k}^{s}= & {} B_{k}^{s} Pr(T=k,S=s) = B_{k}^{s} \mathbb {E}_{x}[Pr(T=k,S=s|r_{k}=x)]\nonumber \\= & {} B_{k}^{s} \int _{0}^{\infty } exp(-\varLambda _{k,PHP}^{s^{\prime }}([0,x^{\alpha ^{s}/\alpha ^{s^{\prime }}})))\nonumber \\&exp(- \sum _{s^{\prime }\in \{LOS,NLOS\}} \varLambda ^{s^{\prime }}_{j,PHP}([0,R_{j}^{s{\prime }}(x) )) )f_{k}^{s}(r_{k}=x)dx \nonumber \\= & {} \int _{0}^{\infty } \varLambda ^{{\prime }s}_{k,PHP}([0,x))exp(-\sum _{j=1}^{2} \sum _{s^{\prime }\in \{LOS,NLOS\}}\varLambda ^{s{\prime }}_{j,PHP}([0,R_{j}^{s{\prime }}(x) )) ) dx \end{aligned}$$

(22)

1.2 2. Proof of Theorem 1

SINR coverage probability is

$$\begin{aligned} P_{C}=Pr(SINR>\tau _{k}) \overset{a}{=} \sum _{k=1}^{2} \sum _{s\in \{LOS,NLOS\}} A_{k}^{s}P_{C_{k}}^{s}(\tau _{k}) \end{aligned}$$

(23)

$P_{C_{k}}^{s}(\tau _{k})$ is calculated as follow

$$\begin{aligned} P_{C_{k}}^{s}(\tau _{k})= & {} \,Pr(SINR>\tau _{k}\mid T=k , S=s)= \mathbb {E}_{x}[Pr(SINR>\tau _{k}\mid T=k , S=s,r_{k}=x)]\nonumber \\= & {} \int _{0}^{\infty } Pr(SINR>\tau _{k}\mid T = k , S=s,r_{k}=x)\times f(r_{k}=x\mid T=k , S=s)dx \end{aligned}$$

(24)

and $f(r_{k}=x\mid T=k , S=s)$ is

$$\begin{aligned} f(r_{k}=x\mid T=k , S=s)&\overset{a}{=}&\frac{Pr(T=k , S=s ,\mid r_{k}=x) f^{s}({r_{k}}=x)}{Pr(T=k , S=s)}\nonumber \\&\overset{b}{=}&\frac{1}{A_{k}^{s}} \varLambda ^{{\prime }s}_{k,PHP}([0,x))exp\left( -\sum _{j=1}^{2} \sum _{s^{\prime }\in \{LOS,NLOS\}}\varLambda ^{s^{\prime }}_{j,PHP}([0,R_{j}^{s^{\prime }}(x) )\right) \end{aligned}$$

(25)

where (a) follows from the Bayes theorem and (b) from Eq. (21) in Appendix 1 . In order to complete our derivation for SINR coverage probability, we derive $Pr(SINR>\tau _{k}\mid T = k , S=s,r_{k}=x)$. Using similar approach in [7], we have

$$\begin{aligned}&Pr(SINR>\tau _{k}\mid T = k , S=s,r_{k}=x)= Pr(SINR_{k}^{s}>\tau _{k}\mid r_{k}=x)\nonumber \\&\quad {\approx } \sum _{n=1}^{\upsilon ^{s}} (-1)^{n+1}\left( {\begin{array}{c}\upsilon ^{s}\\ n\end{array}}\right) \mathbb {E}[exp(-\mu _{k,n}^{s} \sigma ^{2})]L_{I}(\mu _{k,n}^{s}) \end{aligned}$$

(26)

where $\mu _{k,n}^{s}$ was defined in Theorem 1. In order to calculate the Laplace transform of interferences $L_{I}(\mu _{k,n}^{s})=\mathbb {E}[exp(-\mu _{k,n}^{s} I)]$, we define I as following

$$\begin{aligned} I= & {} \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\phi _{1}^{s^{\prime }}\} \backslash BS_{k,0}}} P_{1} |h_{1,i}|^{2} G_{1,i}r_{1,i}^{-\alpha ^{s^{\prime }}}\nonumber \\&+\sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\psi ^{s^{\prime }}\} \backslash BS_{k,0}}} P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s^{\prime }}}\nonumber \\= & {} \sum _{j=1}^{2} \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\phi _{j}^{s^{\prime }}\} \backslash BS_{k,0}}} P_{j} |h_{j,i}|^{2} G_{j,i}r_{j,i}^{-\alpha ^{s^{\prime }}}\nonumber \\&- \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\phi _{2}^{s^{\prime }}\cap \psi ^{s^{{\prime }c}}\}}} P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s^{\prime }}} \end{aligned}$$

(27)

Let us denote

$$\begin{aligned} I_{H} = \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\phi _{2}^{s^{\prime }}\cap \psi ^{s^{{\prime }c}}\}}} P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s^{\prime }}} \end{aligned}$$

(28)

which represents the interference from SBSs of the baseline PPP $\phi _{2}$ who are inside of holes.

Since in this approach, PHP distribution of SBSs ($\psi$) is approximated by the baseline PPP, $\phi _{2}$, $I_{H}=0$. Hence, similar to PPP-based approaches like [7]

$$\begin{aligned}&L_{I}(\mu _{k,n}^{s}) =\mathbb {E}\left[ exp\left( -\mu _{k,n}^{s} \left( \sum _{j=1}^{2} \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\phi _{j}^{s^{\prime }}\}}}P_{j} |h_{j,i}|^{2} G_{j,i}r_{j,i}^{-\alpha ^{s^{\prime }}}\right) \right) \right] \nonumber \\&\quad = \prod _{j=1}^{2} \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( -\int _{R_{j}^{s^{\prime }}(x)}^{\infty } \left( 1- \mathbb {E}\left[ exp\left( -\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s^{\prime }}}\right) \right] \right) \varLambda ^{{\prime }s{\prime }}_{j}([0,r)) dr\right) \end{aligned}$$

(29)

and $\mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s^{\prime }}})]$ is

$$\begin{aligned} \mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s^{\prime }}})]&\overset{a}{=}&\sum _{g=1}^{4} P_{j,g}\mathbb {E}_{|h_{j}|^{2}}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} A_{j,g}r^{-\alpha ^{s^{\prime }}})]\nonumber \\&\overset{b}{=}&\sum _{g=1}^{4} P_{j,g} \left( \frac{1}{1+(\mu _{k,n}^{s}P_{j} A_{j,g}r^{-\alpha ^{s^{\prime }}})/\upsilon ^{s^{\prime }}}\right) ^{\upsilon ^{s^{\prime }}} \end{aligned}$$

(30)

where in (a) expectation are taken over $G_{j}$, $P_{j,g}$ and $A_{j,g}$ are constants defined in Table 2, and step (b) follows from computing the moment generating function of the gamma distributed random variable $|h_{j}|^{2}$. The integration range excludes a ball centered at 0 and radius $R_{j}^{s^{\prime }}(x)=(\frac{P_{j}}{P_{k}}\times \frac{M_{j}}{M_{k}})^{1/\alpha ^{s^{\prime }}}\times x^{\alpha ^{s}/\alpha ^{s^{\prime }}}$ because the closest $s^{\prime }\in \{LOS,NLOS\}$ interferer in $j{\mathrm{th}}$ tier has to be farther than the serving BS, based on cell association rule considered. Finally, by combining the above equations, SINR coverage probability expression given in Theorem 1 is obtained.

1.3 3. Proof of Theorem 2

In the case of incorporating the serving hole, we follow the same approach used in Appendix 2 and Eqs. (23)–(26) are held in this proof too. It is enough to consider the effect of the serving hole in the interference characterization. Therefore, we approximate I as following, which incorporates the serving hole and ignore other holes

$$\begin{aligned} I= & {} \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \bigg \{\sum _{i\in {\{\phi _{1}^{s^{\prime }}\} \backslash BS_{k,0}}} P_{1} |h_{1,i}|^{2} G_{1,i}r_{1,i}^{-\alpha ^{s^{\prime }}}\nonumber \\&+\sum _{i\in {\{\psi ^{s^{\prime }} \cap S^{c}(x,D,\theta _{c})\} \backslash BS_{k,0}}} P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s^{\prime }}}\bigg \} \end{aligned}$$

(31)

where $S(x,D,\theta _{c})$ was defined in Definition 1 and x is the distance between the serving MBS and the typical UE. Now we calculate $L_{I}(\mu _{k,n}^{s})$

$$\begin{aligned}&L_{I}(\mu _{k,n}^{s})\nonumber \\&\quad =\mathbb {E}\left[ exp\left( -\mu _{k,n}^{s} \left( \sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\phi _{1}^{s^{\prime }}\}\backslash BS_{k,0}}} P_{1} |h_{1,i}|^{2} G_{1,i}r_{1,i}^{-\alpha ^{s^{\prime }}} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. +\sum _{s^{\prime }\in {\{LOS,NLOS\}}} \sum _{i\in {\{\psi ^{s^{\prime }} \cap S^{c}(x,D,\theta _{c})\} \backslash BS_{k,0}}}P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s^{\prime }}}\right) \right) \right] \nonumber \\&\quad \overset{a}{=} \prod _{s^{\prime }\in \{{LOS,NLOS}\}} \mathbb {E}\left[ \prod _{i\in {\{\phi _{1}^{s^{\prime }}\} \backslash BS_{k,0}}} exp(-\mu _{k,n}^{s}P_{1} |h_{1,i}|^{2} G_{1,i}r_{1,i}^{-\alpha ^{s^{\prime }}})\right] \nonumber \\&\qquad \prod _{s^{\prime }\in \{{LOS,NLOS}\}} \mathbb {E}\left[ \prod _{i\in {\{\psi ^{s^{\prime }} \cap S^{c}(x,D,\theta _{c})\} \backslash BS_{k,0}}} exp(-\mu _{k,n}^{s}P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s^{\prime }}})\right] \nonumber \\&\quad \overset{b}{=} \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( -\lambda _{1}\int _{\mathbb {R}^2\backslash B(0,R_{1}^{s^{\prime }}(x))} ( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{1} |h_{1}|^{2} G_{1}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS\right) \nonumber \\&\qquad \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( -\lambda _{2}\left( \int _{\mathbb {R}^2\backslash B(0,R_{2}^{s^{\prime }}(x))} ( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})] ) P^{s^{\prime }}(r) dS \right. \right. \nonumber \\&\qquad \left. \left. - \int _{\Xi }(1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS\right) \right) \nonumber \\&\quad = \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( -\int _{R_{1}^{s^{\prime }}(x)}^{\infty } ( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{1} |h_{1}|^{2} G_{1}r^{-\alpha ^{s^{\prime }}})] ) \varLambda ^{{\prime }s{\prime }}_{1}([0,r) dr\right) \nonumber \\&\qquad \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( -\int _{R_{2}^{s^{\prime }}(x)}^{\infty }( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})] ) \varLambda ^{{\prime }s{\prime }}_{2}([0,r) dr\right) \nonumber \\&\qquad \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( \lambda _{2} \int _{\Xi }(1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS\right) \nonumber \\&\quad =\prod _{j=1}^{2} \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( -\int _{R_{j}^{s^{\prime }}(x)}^{\infty } ( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s^{\prime }}})] ) \varLambda ^{{\prime }s{\prime }}_{j}([0,r) dr\right) \nonumber \\&\qquad \prod _{s^{\prime }\in \{{LOS,NLOS}\}} exp\left( \lambda _{2} \int _{\Xi }(1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS\right) \end{aligned}$$

(32)

where (a) is due to the independence assumption among tiers and LOS/NLOS BSs in each tier and (b) follows from the PGFL of a PPP. $\Xi = S(x,D,\theta _{c})\bigcap B^{c}(0,R_{2}^{s^{\prime }}(x))$ and $B^{c}(0,R_{2}^{s^{\prime }}(x))$ represent regions that are outside of a ball centered at the origin with radius $R_{2}^{s^{\prime }}(x) = (\frac{P_{2}}{P_{k}}\times \frac{M_{2}}{M_{k}})^{1/\alpha ^{s^{\prime }}}\times x^{\alpha ^{s}/\alpha ^{s^{\prime }}}$.

Fig. 11

Illustration of the effect of a hole in the interference characterization

Next, we need to calculate $\int _{\Xi } (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS$. For this, we use transformation as below

$$\begin{aligned} r=\sqrt{u^{2}+x^{2}-2uxcos(\phi )} \end{aligned}$$

(33)

where the above equation is derived based on cosine-law, u and $\phi$ is defined in Fig. 11.

Following discussion in Remark 2, we approximate

$\Xi$ to $S(x,D,\theta _{c})$. So, $\int _{ \Xi } (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS$ is

$$\begin{aligned}&\int _{\Xi } (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS)\nonumber \\&\quad \approx \int _{t}^{t+\theta _{c}} \int _{0}^{D} (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{j} |h_{2}|^{2} G_{2}(u^{2}+x^{2}-2uxcos(\phi ))^{-\alpha ^{s^{\prime }}/2})])\nonumber \\&\qquad P^{s^{\prime }}(\sqrt{u^{2}+x^{2}-2uxcos(\phi )}) udud\phi ) \end{aligned}$$

(34)

Since the direction of circular sectors have a uniform distribution in $[0,2\pi )$, we have

$$\begin{aligned}&\int _{\Xi } (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s^{\prime }}})]) P^{s^{\prime }}(r) dS)\nonumber \\&\quad \approx \int _{0}^{2\pi } \int _{t}^{t+\theta _{c}} \int _{0}^{D} (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{j} |h_{2}|^{2} G_{2}(u^{2}+x^{2}-2uxcos(\phi ))^{-\alpha ^{s^{\prime }}/2})])\nonumber \\&\qquad P^{s^{\prime }}(\sqrt{u^{2}+x^{2}-2uxcos(\phi )}) \frac{1}{2\pi } udud\phi dt)\nonumber \\&\quad \overset{a}{=} \frac{\theta _{c}}{2\pi } \int _{0}^{2\pi } \int _{0}^{D} (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{j} |h_{2}|^{2} G_{2}(u^{2}+x^{2}-2uxcos(\phi ))^{-\alpha ^{s^{\prime }}/2})])\nonumber \\&\qquad P^{s^{\prime }}(\sqrt{u^{2}+x^{2}-2uxcos(\phi )}) udud\phi ) \end{aligned}$$

(35)

where (a) is derived by substituting integrals and using this fact that integrand function is periodic respect to $\phi$ with period $2\pi$. The above two-fold integral represents area of circular hole. Compring results derived in [17] for circular holes and using similar approach in Eq. (30) to derive $\mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}(u^{2}+x^{2}-2uxcos(\phi ))^{-\alpha ^{s^{\prime }}/2})]$, this integral can be expressed as follow

$$\begin{aligned} \int _{x-D}^{x+D} F(\upsilon ^{s^{\prime }} , \frac{\mu _{k,n}^{s} P_{2}A_{2,g}u^{-\alpha ^{s^{\prime }}} }{\upsilon ^{s^{\prime }}}) 2\pi \lambda (u) P^{s'}(u) udu \end{aligned}$$

(36)

where $\lambda (u)$ is defined in Theorem 2. Therefore, SINR coverage probability by incorporating serving hole can be expressed as Theorem 2.

1.4 4. Proof of Theorem 3

Similar to the proof used in Appendix 3, the approximation of the interference in this case is

$$\begin{aligned} I= \sum _{s'\in {\{LOS,NLOS\}}} \bigg \{\sum _{i\in {\{\phi _{1}^{s'}\} \backslash BS_{k,0}}} P_{1} |h_{1,i}|^{2} G_{1,i}r_{1,i}^{-\alpha ^{s'}} + \sum _{i\in {\{\psi ^{s'} \cap \Omega ^{c}\} \backslash BS_{k,0}}} P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s'}}\bigg \} \end{aligned}$$

(37)

where $\Omega = \bigcup _{ s^{\prime \prime }\in {\{LOS,NLOS\}} } S(y,D,\theta _{c})$ and y is the distance between $s^{\prime \prime }\in {\{LOS,NLOS\}}$ interferer MBS and the typical UE. We ignore possible overlaps between two holes and approximate $\Omega$ as $\Omega \approx \sum _{ s^{\prime \prime }\in {\{LOS,NLOS\}} } S(y,D,\theta _{c})$. Similar to Eq. (32), $L_{I}(\mu _{k,n}^{s})$ is

$$\begin{aligned}&L_{I}(\mu _{k,n}^{s}|y) \nonumber \\&\quad = \prod _{j=1}^{2} \prod _{s'\in \{{LOS,NLOS}\}} exp\left( -\int _{R_{j}^{s'}(x)}^{\infty } ( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s'}})] ) \varLambda '^{s'}_{j}([0,r) dr\right) \nonumber \\&\qquad \prod _{s'\in \{{LOS,NLOS}\}} exp(\lambda _{2} \int _{\Omega }(1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS) \end{aligned}$$

(38)

Note that the exact region for the integral is $\Omega \bigcap B^{c}(0,R_{2}^{s'}(x))$, but we approximate it by $\Omega$. Similar to proof in Appendix 3, $\int _{\Omega } (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS$ can be calculated as below

$$\begin{aligned}&\int _{\Omega } (1- \mathbb {E}[exp(-\mu _{1,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS\nonumber \\&\quad \approx \sum _{s^{\prime \prime }\in \{{LOS,NLOS}\}} \frac{\theta _{c}}{2\pi } \int _{0}^{2\pi } \int _{0}^{D} (1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}(u^{2}+y^{2}-2uycos(\phi ))^{-\alpha ^{s'}/2})])\nonumber \\&\qquad P^{s'}(\sqrt{u^{2}+y^{2}-2uycos(\phi )})udud\phi \end{aligned}$$

(39)

Now, to complete our derivation, we need to calculate PDF of y. Given that the typical UE is associated with a $s\in \{LOS,NLOS\}$ BS in $k{\mathrm{th}}$ tier at distance $r_{k}=x$ and observe at least one $s^{\prime \prime }\in \{LOS,NLOS\}$ MBS, CCDF of y is

$$\begin{aligned}&\bar{F}^{s{\prime \prime }}(y|T=k,S=s,r_{k}=x)= Pr(Y>y|T=k,S=s,r_{k}=x) \nonumber \\&\quad = Pr(\mathbb {N}(B(0,y) \backslash B(0,R_{1}^{s{\prime \prime }}(x)) =\varnothing )=\frac{ exp(-\varLambda _{1}^{s{\prime \prime }}([0,y)))exp(\varLambda _{1}^{s{\prime \prime }}([0,R_{1}^{s{\prime \prime }}(x))))}{1-exp(-\varLambda _{1}([R_{1}^{s{\prime \prime }}(x),\infty )))} \end{aligned}$$

(40)

where $\mathbb {N}$ represents the number of points in $\phi _{1}$ that are in the desired set. PDF of y now follows by differentiating the above expression

$$\begin{aligned}&f^{s{\prime \prime }}(y|T=k,S=s,r_{k}=x)= -\dfrac{d}{dy}\bar{F}^{s{\prime \prime }}(y|T=k,S=s,r_{k}=x)\nonumber \\&\quad =\frac{\varLambda ^{{\prime }s{\prime \prime }}_{1}([0,y)) exp(-\varLambda _{1}^{s{\prime \prime }}([0,y))+\varLambda _{1}^{s{\prime \prime }}([0,R_{1}^{s{\prime \prime }}(x))))}{1-exp(-\varLambda _{1}([R_{1}^{s{\prime \prime }}(x),\infty )))} \end{aligned}$$

(41)

Finally $L_{I}(\mu _{k,n}^{s})$ can be expressed as

$$\begin{aligned}&L_{I}(\mu _{k,n}^{s}) \nonumber \\&\quad = \prod _{j=1}^{2} \prod _{s'\in \{{LOS,NLOS}\}} exp\left( -\int _{R_{j}^{s'}(x)}^{\infty }( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s'}})] ) \varLambda '^{s'}_{j}([0,r)) dr\right) \nonumber \\&\qquad \prod _{s'\in \{{LOS,NLOS}\}} \prod _{s^{\prime \prime }\in \{{LOS,NLOS}\}}\nonumber \\&\qquad \int _{R_{1}^{s{\prime \prime }}(x)}^{\infty }exp\left( \frac{\theta _{c}}{2\pi }\lambda _{2} \int _{0}^{2\pi } \int _{0}^{D}(1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}(u^{2}+y^{2}-2uycos(\phi ))^{-\alpha ^{s'}/2})]\right) \nonumber \\&\qquad P^{s'}(\sqrt{u^{2}+y^{2}-2uycos(\phi )})udud\phi )f^{s{\prime \prime }}(y|T=k,S=s,r_{k}=x)dy \end{aligned}$$

(42)

Similar to Eq. (30), $\mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s'}})]$ and $\mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}(u^{2}+y^{2}-2uycos(\phi ))^{-\alpha ^{s'}/2})]$ can be calculated. Therefore, SINR coverage probability by incorporating the nearest non-sering LOS and NLOS can be obtained.

1.5 5. Proof of Theorem 4

The exact expression for the interference in our proposed two-tier HCN model is

$$\begin{aligned} I= \sum _{s'\in {\{LOS,NLOS\}}} \bigg \{\sum _{i\in {\{\phi _{1}^{s'}\} \backslash BS_{k,0}}} P_{1} |h_{1,i}|^{2} G_{1,i}r_{1,i}^{-\alpha ^{s'}} + \sum _{i\in {\{\phi _{2}^{s'} \cap \Gamma ^{c}\} \backslash BS_{k,0}}} P_{2} |h_{2,i}|^{2} G_{2,i}r_{2,i}^{-\alpha ^{s'}}\bigg \} \end{aligned}$$

(43)

where $\Gamma = \bigcup _{y\in {\phi _{1}}} S(y,D,\theta _{c})$. However, due to the possible overlaps between the holes, the exact characterization of I is complex. Therefore, we approximate $\Gamma$ to $\Gamma \approx \sum _{s^{\prime \prime }\in {\{LOS,NLOS\}}} \sum _{y\in {\phi _{1}^{s{\prime \prime }}}} S(y,D,\theta _{c})$, which ignores possible overlaps between the holes. Using this assumption, $L_{I}(\mu _{k,n}^{s})$ can be evaluated as

$$\begin{aligned}&L_{I}(\mu _{k,n}^{s}) \nonumber \\&\quad \approx \prod _{j=1}^{2} \prod _{s'\in {\{LOS,NLOS\}}} exp\left( -\int _{R_{j}^{s'}(x)}^{\infty }( 1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{j} |h_{j}|^{2} G_{j}r^{-\alpha ^{s'}})] ) \varLambda '^{s'}_{j}([0,r) dr\right) \nonumber \\&\qquad \prod _{s'\in \{{LOS,NLOS}\}} \mathbb {E}_{\phi _{1}} \left[ exp\left( \lambda _{2} \int _{\Gamma }(1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS\right) \right] \nonumber \\&\quad \approx exp \left( -\sum _{j=1}^{2} \sum _{s'\in \{LOS,NLOS\}} W_{j}^{s'}(x)\right) \prod _{s'\in \{{LOS,NLOS}\}}\nonumber \\&\qquad \mathbb {E}_{\phi _{1}^{s{\prime \prime }}} \left[ exp\left( \sum _{s^{\prime \prime }\in {\{LOS,NLOS\}}} \sum _{y\in {\phi _{1}^{s{\prime \prime }}}} \lambda _{2} \int _{S(y,D,\theta _{c})} (1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS\right) \right] \nonumber \\&\quad \approx exp \left( -\sum _{j=1}^{2} \sum _{s'\in \{LOS,NLOS\}} W_{j}^{s'}(x)\right) \prod _{s'\in \{{LOS,NLOS}\}} \prod _{s^{\prime \prime }\in \{{LOS,NLOS}\}}\nonumber \\&\qquad \mathbb {E}_{\phi _{1}^{s{\prime \prime }}} \left[ \prod _{y\in {\phi _{1}^{s{\prime \prime }}}} exp\left( \lambda _{2}\int _{S(y,D,\theta _{c})} (1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS\right) \right] \nonumber \\&\quad \approx exp \left( -\sum _{j=1}^{2} \sum _{s'\in \{LOS,NLOS\}} W_{j}^{s'}(x)\right) \prod _{s'\in \{{LOS,NLOS}\}} \prod _{s^{\prime \prime }\in \{{LOS,NLOS}\}}\nonumber \\&\qquad exp\left( -\int _{R_{1}^{s{\prime \prime }}(x)}^{\infty } (1- exp( \lambda _{2}\int _{S(y,D,\theta _{c})} (1- \mathbb {E}[exp(-\mu _{k,n}^{s}P_{2} |h_{2}|^{2} G_{2}r^{-\alpha ^{s'}})]) P^{s'}(r) dS)]))\varLambda _{1}^{s{\prime \prime }}([0,y)) dy \right) \nonumber \\&\quad \approx exp \left( -\sum _{j=1}^{2} \sum _{s'\in \{LOS,NLOS\}} W_{j}^{s'}(x)\right) \nonumber \\&\qquad exp\left( - \sum _{ s^{\prime \prime }\in {\{LOS,NLOS\}} } \int _{R_{1}^{s{\prime \prime }}(x)}^{\infty }\sum _{ s'\in {\{LOS,NLOS\}} } (1-exp(Q^{s'}(y)) ) \varLambda _{1}^{s{\prime \prime }}([0,y)) dy \right) \end{aligned}$$

(44)

Note that similar to prior proofs, the exact region for the integral is $\Gamma \cap B^{c}(0,R_{2}^{s'}(x))$, but we approximate it by $\Gamma$.