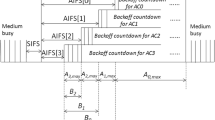
Appendix 1: The component matrices of the transition probability matrix \({\varvec{P}}\)
.
Let \(W=(2^{m+1}-1)W_0+(m+1)(M-1)\), we have
$$\begin{array}{*{20}l} {{\bar{\user2 C}}_{0} = \left( {r_{0}^{{(T_{f} )}} } \right),} \hfill \\ {{\bar{\user2 C}}_{1} = \left( {\begin{array}{*{20}c} {\user2{C}_{{10}} } \\ {\user2{C}_{{11}} } \\ \vdots \\ {\user2{C}_{{1m}} } \\ \end{array} } \right)_{{W \times 1}} ,} \hfill \\ {C_{{1i}} = \left( {\begin{array}{*{20}c} {(1 - p)qa_{0}^{{i*}} } \\ 0 \\ \vdots \\ 0 \\ {qr_{0}^{{(T_{f} )}} } \\ \vdots \\ {qr_{0}^{{(T_{f} )}} } \\ \end{array} } \right)_{{(W_{i} + M - 1) \times 1}} (0 \le i \le m).} \hfill \\ {C_{2} = \left( {\begin{array}{*{20}c} {\user2{C}_{{20}} } & 0 & \cdots & 0 \\ \user2{C} & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {\user2{C}_{{2m}} } & 0 & \cdots & 0 \\ \end{array} } \right)_{{W \times W,}} } \hfill \\ \end{array}$$
where
$$\begin{aligned} {\varvec{C}}_{2i}= {} \left( \begin{array}{ccc|ccccccc} (1-p)qa^{i*}_0\frac{1}{W_0} {} \cdots {} (1-p)qa^{i*}_0\frac{1}{W_0} {} 0 {} \cdots {} 0\\ 0 {} \cdots {} 0 {} \vdots {} \ddots {} \vdots \\ \vdots {} \ddots {} \vdots {} \vdots {} \ddots {} \vdots \\ 0 {} \cdots {} 0 {} 0 {} \cdots {} 0 \\ \hline qr_0^{(T_f)}\frac{1}{W_0} {} \cdots {} qr_0^{(T_f)}\frac{1}{W_0} {} 0 {} \cdots {} 0\\ \vdots {} \ddots {} \vdots {} \cdots {} \vdots \\ qr_0^{(T_f)}\frac{1}{W_0} {} \cdots {} qr_0^{(T_f)}\frac{1}{W_0} {} 0 {} \cdots {} 0\\ \end{array} \right) _{(W_i+M-1)\times (W_0+M-1)} (0\le i\le m).\\ \overline{{\varvec{A}}}_k= {} \left( {\varvec{A}}_{k0}, {\varvec{A}}_{k1}, \cdots , {\varvec{A}}_{km} \right) _{1\times W} \end{aligned}$$
where for \(i=0, 1,\cdots , m\)
$$\begin{aligned} {\varvec{A}}_{k0}& = \left( r_0^{(T_f)}\frac{1}{W_0}\ \cdots \ r_0^{(T_f)}\frac{1}{W_0}\ |\ 0 \cdots 0\right) _{1\times (W_0+M-1)} , {\varvec{A}}_{ki}=\left( 0 \cdots 0 \right) _{1\times (W_i+M-1)}. \\ {\varvec{B}}_k& = \left( \begin{array}{ccccccc} {\varvec{E}}^{(k)}_{0} &{} {\varvec{F}}_{1}^{(k)} &{} \mathbf{0} &{} \cdots &{} \mathbf{0} &{} \mathbf{0} \\ {\varvec{E}}^{(k)}_{1} &{} {\varvec{H}}_{1}^{(k)} &{}{\varvec{F}}_{2}^{(k)}&{} \cdots &{} \mathbf{0}&{} \mathbf{0}\\ {\varvec{E}}^{(k)}_{2} &{} {\varvec{0}} &{}{\varvec{H}}_{2}^{(k)}&{} \cdots &{} \mathbf{0} &{} \mathbf{0}\\ \vdots &{} \vdots &{}\vdots &{} \ddots &{} \vdots &{} \vdots \\ {\varvec{E}}^{(k)}_{m-1} &{} {\varvec{0}} &{}{\varvec{0}} &{} \cdots &{} {\varvec{H}}_{m-1}^{(k)} &{} {\varvec{F}}_{m}^{(k)}\\ {\varvec{E}}_{m}^{(k)} &{} {\varvec{0}} &{} \mathbf{0} &{} \cdots &{} \mathbf{0} &{} {\varvec{H}}_{m}^{(k)} \\ \end{array} \right) _{W\times W} \end{aligned}$$
where
$$\begin{aligned} {\varvec{E}}^{(k)}_{0}& = \left( \begin{array}{cc} {\varvec{E}}^{1}_{0} &{} {\varvec{E}}^{3}_{0} \\ {\varvec{E}}^{2}_{0} &{} {\varvec{E}}^{4}_{0} \end{array} \right) \\ {\varvec{E}}^{1}_{0}& = \left( \begin{array}{ccccc} (1-p)qa_{k}^{0*}\frac{1}{W_{0}} &{} (1-p)qa_{k}^{0*}\frac{1}{W_{0}} &{} \cdots &{} \cdots &{} (1-p)qa_{k}^{0*}\frac{1}{W_{0}} \\ r_{k-1}^{(\sigma )} \overline{\beta _{1}^{0}} + r_{k-1}^{(\sigma + T)}\beta _{1}^{0} &{} 0 &{} \cdots &{} 0 &{} 0 \\ 0 &{} r_{k-1}^{(\sigma )} \overline{\beta _{2}^{0}} + r_{k-1}^{(\sigma + T)}\beta _{2}^{0} &{} \ddots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} r_{k-1}^{(\sigma )} \overline{\beta _{W_{0}-1}^{0}} + r_{k-1}^{(\sigma + T)}\beta _{W_{0}-1}^{0} &{} 0 \end{array} \right) _{W_{0} \times W_{0}}\\ {\varvec{E}}^{2}_{0}& = \left( \begin{array}{ccc} qr_{k}^{(T_{f})}\frac{1}{W_{0}} &{} \cdots &{} qr_{k}^{(T_{f})}\frac{1}{W_{0}} \\ \vdots &{} \ddots &{} \vdots \\ qr_{k}^{(T_{f})}\frac{1}{W_{0}} &{} \cdots &{} qr_{k}^{(T_{f})}\frac{1}{W_{0}} \end{array} \right) _{(M-1) \times W_{0}} \\ {\varvec{E}}^{3}_{0}& = \left( \begin{array}{cccc} (1-p)(1-q)a_{k-1}^{0*} &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 \end{array} \right) _{W_{0} \times (M-1)}\\ {\varvec{E}}^{4}_{0}& = \left( \begin{array}{ccccc} 0 &{} (1-q)r_{k-1}^{(T_{f})} &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} &{} \ddots &{} (1-q)r_{k-1}^{(T_{f})} \\ 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{(M-1) \times (M-1)}.\\ {\varvec{E}}^{(k)}_{i}& = \left( \begin{array}{cc} {\varvec{E}}^{1}_{i} &{} {\varvec{0}} \\ {\varvec{E}}^{2}_{i} &{} {\varvec{0}} \end{array} \right) , \quad 1\le i \le m\\ {\varvec{E}}^{1}_{i}& = \left( \begin{array}{ccc} (1-p)qa_{k}^{i*}\frac{1}{W_{0}} &{} \cdots &{} (1-p)qa_{k}^{i*}\frac{1}{W_{0}} \\ 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \end{array} \right) _{W_{i} \times W_{0}} \\ {\varvec{E}}^{2}_{i}& = \left( \begin{array}{ccc} qr_{k}^{(T_{f})}\frac{1}{W_{0}} &{} \cdots &{} qr_{k}^{(T_{f})}\frac{1}{W_{0}} \\ \vdots &{} \ddots &{} \vdots \\ qr_{k}^{(T_{f})}\frac{1}{W_{0}} &{} \cdots &{} qr_{k}^{(T_{f})}\frac{1}{W_{0}} \end{array} \right) _{(M-1) \times W_{0}}\\ {\varvec{F}}^{(k)}_{i}& = \left( \begin{array}{cc} {\varvec{F}}^{1}_{i} &{} {\varvec{0}} \\ {\varvec{E}}^{2}_{i} &{} {\varvec{0}} \end{array} \right) , \quad 1\le i \le m \end{aligned}$$
$$\begin{aligned} {\varvec{F}}^{1}_{i}& = \left( \begin{array}{ccc} pa_{k-1}^{(i-1)c}\frac{1}{W_{i}} &{} \cdots &{} pa_{k-1}^{(i-1)c}\frac{1}{W_{i}} \\ 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \end{array} \right) _{W_{i-1} \times W_{i}} \\ {\varvec{E}}^{2}_{i}& = \left( \begin{array}{ccc} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \\ (1-q)r_{k-1}^{(T_{f})}\frac{1}{W_{i}} &{} \cdots &{} (1-q)r_{k-1}^{(T_{f})}\frac{1}{W_{i}} \end{array} \right) _{(M-1) \times W_{i}}\\ {\varvec{H}}^{(k)}_{i}& = \left( \begin{array}{cc} {\varvec{H}}^{1}_{i} &{} {\varvec{H}}^{3}_{i} \\ {\varvec{0}} &{} {\varvec{H}}^{4}_{i} \end{array} \right) , 1\le i \le m-1\\ {\varvec{H}}^{1}_{i}& = \left( \begin{array}{ccccc} 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \\ r_{k-1}^{(\sigma )}\overline{\beta _{1}^{i}} + r_{k-1}^{(\sigma + T)}\beta _{1}^{i} &{} \ddots &{} &{} &{} \vdots \\ 0 &{} r_{k-1}^{(\sigma )}\overline{\beta _{2}^{i}} + r_{k-1}^{(\sigma + T)}\beta _{2}^{i} &{} \ddots &{} &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 &{} r_{k-1}^{(\sigma )}\overline{\beta _{W_{i}-1}^{i}} + r_{k-1}^{(\sigma + T)}\beta _{W_{i}-1}^{i} &{} 0 \end{array} \right) _{W_{i} \times W_{i}}\\ {\varvec{H}}^{3}_{i}& = \left( \begin{array}{cccc} (1-p)(1-q)a_{k-1}^{i*} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \cdots &{} \cdots &{} 0 \\ \vdots &{} &{} &{} \vdots \\ 0 &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{W_{i} \times (M-1)}\\ {\varvec{H}}^{4}_{i}& = \left( \begin{array}{ccccc} 0 &{} (1-q)r_{k-1}^{(T_{f})} &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} &{} \ddots &{} (1-q)r_{k-1}^{(T_{f})} \\ 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{(M-1) \times (M-1)}\\ {\varvec{H}}^{(k)}_{m}& = \left( \begin{array}{cc} {\varvec{H}}_{m}^{1} &{} {\varvec{H}}_{m}^{3} \\ {\varvec{H}}_{m}^{2} &{} {\varvec{H}}_{m}^{4} \end{array} \right) \\ {\varvec{H}}_{m}^{1}& = \left( \begin{array}{ccccc} pa_{k-1}^{mc}\frac{1}{W_{m}} &{} pa_{k-1}^{mc}\frac{1}{W_{m}} &{} \cdots &{} \cdots &{} pa_{k-1}^{mc}\frac{1}{W_{m}} \\ r_{k-1}^{(\sigma )}\overline{\beta _{1}^{m}} + r_{k-1}^{(\sigma + T)}\beta _{1}^{m} &{} \ddots &{} &{} &{} \vdots \\ 0 &{} r_{k-1}^{(\sigma )}\overline{\beta _{2}^{m}} + r_{k-1}^{(\sigma + T)}\beta _{2}^{m} &{} \ddots &{} &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 &{} r_{k-1}^{(\sigma )}\overline{\beta _{W_{m}-1}^{m}} + r_{k-1}^{(\sigma + T)}\beta _{W_{m}-1}^{m} &{} 0 \end{array} \right) _{W_{m} \times W_{m}}\\ {\varvec{H}}_{m}^{2}& = \left( \begin{array}{ccc} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \\ (1-q)r_{k-1}^{(T_{f})}\frac{1}{W_{m}} &{} \cdots &{} (1-q)r_{k-1}^{(T_{f})}\frac{1}{W_{m}} \end{array} \right) _{(M-1) \times W_{m}} \end{aligned}$$
$$\begin{aligned} {\varvec{H}}_{m}^{3}& = \left( \begin{array}{cccc} (1-p)(1-q)a_{k-1}^{m*} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \cdots &{} \cdots &{} 0 \\ \vdots &{} &{} &{} \vdots \\ 0 &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{W_{m} \times (M-1)}\\ {\varvec{H}}_{m}^{4}& = \left( \begin{array}{ccccc} 0 &{} (1-q)r_{k-1}^{(T_{f})} &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} &{} \ddots &{} (1-q)r_{k-1}^{(T_{f})} \\ 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{(M-1) \times (M-1).} \end{aligned}$$
Appendix 2: The component matrices of the matrix \({\varvec{B(z)}}\)
.
$$\begin{aligned} {\varvec{E}}_0(z)& = \left( \begin{array}{cc} {\varvec{E}}_{0}^{1}(z) &{} {\varvec{E}}_{0}^{3}(z) \\ {\varvec{E}}_{0}^{2}(z) &{} {\varvec{E}}_{0}^{4}(z) \end{array} \right) \\ {\varvec{E}}_{0}^{1}(z)& = \left( \begin{array}{ccccc} (1-p)qa^{0*}(z)\frac{1}{W_{0}} &{} (1-p)qa^{0*}(z)\frac{1}{W_{0}} &{} \cdots \\ r^{(\sigma )}(z) \overline{\beta _{1}^{0}} + r^{(\sigma + T)}(z)\beta _{1}^{0} &{} 0 &{} \cdots \\ 0 &{} r^{(\sigma )}(z) \overline{\beta _{2}^{0}} + r^{(\sigma + T)}(z)\beta _{2}^{0} &{} \ddots \\ \vdots &{} \vdots &{} \ddots \\ 0 &{} 0 &{} \cdots \end{array} \right. \\&\left. \begin{array}{cccccc} \cdots &{} (1-p)qa^{0*}(z)\frac{1}{W_{0}} \\ 0 &{} 0 \\ 0 &{} 0 \\ \vdots &{} \vdots \\ r^{(\sigma )}(z) \overline{\beta _{W_{0}-1}^{0}} + r^{(\sigma + T)}(z)\beta _{W_{0}-1}^{0} &{} 0 \\ \end{array} \right) _{W_{0} \times W_{0}}\\ {\varvec{E}}_{0}^{2}(z)& = \left( \begin{array}{ccc} qr^{(T_{f})}(z)\frac{1}{W_{0}} &{} \cdots &{} qr^{(T_{f})}(z)\frac{1}{W_{0}} \\ \vdots &{} \ddots &{} \vdots \\ qr^{(T_{f})}(z)\frac{1}{W_{0}} &{} \cdots &{} qr^{(T_{f})}(z)\frac{1}{W_{0}} \end{array} \right) _{(M-1) \times W_{0}}\\ {\varvec{E}}_{0}^{3}(z)& = \left( \begin{array}{cccc} (1-p)(1-q)a^{0*}(z) &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 \end{array} \right) _{W_{0} \times (M-1)}\\ {\varvec{E}}_{0}^{4}(z)& = \left( \begin{array}{ccccc} 0 &{} (1-q)r^{(T_{f})}(z) &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} &{} \ddots &{} (1-q)r^{(T_{f})}(z) \\ 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{(M-1) \times (M-1)}\\ {\varvec{E}}_{i}(z)& = \left( \begin{array}{cc} {\varvec{E}}_{i}^{1}(z) &{} \mathbf{0} \\ {\varvec{E}}_{i}^{2}(z) &{} \mathbf{0} \end{array} \right) (1\le i \le m) \\ {\varvec{E}}_{i}^{1}(z)& = \left( \begin{array}{ccc} (1-p)qa^{i*}(z)\frac{1}{W_{0}} &{} \cdots &{} (1-p)qa^{i*}(z)\frac{1}{W_{0}} \\ 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \end{array} \right) _{W_{i} \times W_{0}} \\ {\varvec{E}}_{i}^{2}(z)& = \left( \begin{array}{ccc} qr^{(T_{f})}(z)\frac{1}{W_{0}} &{} \cdots &{} qr^{(T_{f})}(z)\frac{1}{W_{0}} \\ \vdots &{} \ddots &{} \vdots \\ qr^{(T_{f})}(z)\frac{1}{W_{0}} &{} \cdots &{} qr^{(T_{f})}(z)\frac{1}{W_{0}} \end{array} \right) _{(M-1) \times W_{0}} \\ {\varvec{F}}_{i}(z)& = z\left( \begin{array}{cc} {\varvec{E}}_{i}^{1}(z) &{} \mathbf{0} \\ {\varvec{E}}_{i}^{2}(z) &{} \mathbf{0} \end{array} \right) (1\le i \le m) \end{aligned}$$
$$\begin{aligned} {\varvec{F}}_{i}^{1}(z)& = \left( \begin{array}{ccc} pa^{(i-1)c}(z)\frac{1}{W_{i}} &{} \cdots &{} pa^{(i-1)c}(z)\frac{1}{W_{i}} \\ 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \end{array} \right) _{W_{i-1} \times W_{i}} \\ {\varvec{F}}_{i}^{2}(z)& = \left( \begin{array}{ccc} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \\ (1-q)r^{(T_{f})}(z)\frac{1}{W_{i}} &{} \cdots &{} (1-q)r^{(T_{f})}(z)\frac{1}{W_{i}} \end{array} \right) _{(M-1) \times W_{i}} \\ {\varvec{H}}_{i}(z)& = z\left( \begin{array}{cc} {\varvec{H}}_{i}^{1}(z) &{} {\varvec{H}}_{i}^{3}(z) \\ \mathbf{0} &{} {\varvec{H}}_{i}^{4}(z) \end{array} \right) (1\le i \le m-1) \\ {\varvec{H}}_{i}^{1}(z)& = \left( \begin{array}{ccccc} 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \\ r^{(\sigma )}(z)\overline{\beta _{1}^{i}} + r^{(\sigma + T)}(z)\beta _{1}^{i} &{} \ddots &{} &{} &{} \vdots \\ 0 &{} r^{(\sigma )}(z)\overline{\beta _{2}^{i}} + r^{(\sigma + T)}(z)\beta _{2}^{i} &{} \ddots &{} &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 &{} r^{(\sigma )}(z)\overline{\beta _{W_{i}-1}^{i}} + r^{(\sigma + T)}(z)\beta _{W_{i}-1}^{i} &{} 0 \end{array} \right) _{W_{i} \times W_{i}} \\ {\varvec{H}}_{i}^{3}(z)& = \left( \begin{array}{cccc} (1-p)(1-q)a^{i*}(z) &{} 0 &{} \cdots &{} 0 \\ 0 &{} \cdots &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{W_{i} \times (M-1)} \\ {\varvec{H}}_{i}^{4}(z)& = \left( \begin{array}{ccccc} 0 &{} (1-q)r^{(T_{f})}(z) &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} &{} \ddots &{} (1-q)r^{(T_{f})}(z) \\ 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{(M-1) \times (M-1)} \\ {\varvec{H}}_{m}(z)& = z\left( \begin{array}{cc} {\varvec{H}}_{m}^{1}(z) &{} {\varvec{H}}_{m}^{3}(z) \\ {\varvec{H}}_{m}^{2}(z) &{} {\varvec{H}}_{m}^{4}(z) \end{array} \right) \end{aligned}$$
$$\begin{aligned} {\varvec{H}}_{m}^{1}(z)& = \left( \begin{array}{ccccc} pa^{mc}(z)\frac{1}{W_{m}} &{} pa^{mc}(z)\frac{1}{W_{m}} &{} \cdots \\ r^{(\sigma )}(z)\overline{\beta _{1}^{m}} + r^{(\sigma + T)}(z)\beta _{1}^{m} &{} 0 &{} \\ 0 &{} r^{(\sigma )}(z)\overline{\beta _{2}^{m}} + r^{(\sigma + T)}(z)\beta _{2}^{m} &{} \ddots \\ \vdots &{} \ddots &{} \ddots \\ 0 &{} \cdots &{} 0 \end{array} \right. \\&\left. \begin{array}{cccc} \cdots &{} pa^{mc}(z)\frac{1}{W_{m}} \\ \vdots &{} \vdots \\ \ddots &{} \vdots \\ \ddots &{} \vdots \\ r^{(\sigma )}(z)\overline{\beta _{W_{m}-1}^{m}} + r^{(\sigma + T)}(z)\beta _{W_{m}-1}^{m} &{} 0 \end{array} \right) _{W_{m} \times W_{m}} \\ {\varvec{H}}_{m}^{2}(z)& = \left( \begin{array}{ccc} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 \\ (1-q)r^{(T_{f})}(z)\frac{1}{W_{m}} &{} \cdots &{} (1-q)r^{(T_{f})}(z)\frac{1}{W_{m}} \end{array} \right) _{(M-1) \times W_{m}} \\ {\varvec{H}}_{m}^{3}(z)& = \left( \begin{array}{cccc} (1-p)(1-q)a^{m*}(z) &{} 0 &{} \cdots &{} 0 \\ 0 &{} \cdots &{} \cdots &{} 0 \\ \vdots &{} &{} &{} \vdots \\ 0 &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{W_{m} \times (M-1)}\\ {\varvec{H}}_{m}^{4}(z)& = \left( \begin{array}{ccccc} 0 &{} (1-q)r^{(T_{f})}(z) &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} &{} \ddots &{} (1-q)r^{(T_{f})}(z) \\ 0 &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{array} \right) _{(M-1) \times (M-1)} \end{aligned}$$
where
$$\begin{aligned}&\begin{array}{llll} a^{i*}(z) &{}\equiv \displaystyle \sum ^{\infty }_{k=0}z^{k}a^{i*}_{k}= \displaystyle \sum ^{N-1}_{n^{*}=0}\alpha ^{i}_{n^{*}} e^{-\lambda ((n^{*}+1)\sigma +T)(1-z)} \\ a^{ic}(z) &{}\equiv \displaystyle \sum ^{\infty }_{k=0}z^{k}a^{ic}_{k} = \displaystyle \sum ^{N-1}_{n^{*}=0}\alpha ^{i}_{n^{*}} e^{-\lambda ((n^{*}+1)\sigma + T + (M-1)T_{f})(1-z)} \end{array}\\&\begin{array}{llll} r^{(T_{f})}(z) \equiv \displaystyle \sum ^{\infty }_{k=0}z^{k}r^{(T_{f})}_{k}= e^{-\lambda T_{f}(1-z)}, r^{(\sigma )}(z) \equiv \displaystyle \sum ^{\infty }_{k=0}z^{k}r^{(\sigma )}_{k} = e^{-\lambda \sigma (1-z)} \\ r^{(\sigma +T)}(z) \equiv \displaystyle \sum ^{\infty }_{k=0}z^{k}r^{(\sigma +T)}_{k}= e^{-\lambda (\sigma +T)(1-z)}. \end{array} \end{aligned}$$
Appendix 3: The algorithm computing the matrices \({\varvec{V}}_k\)
. Rewrite the formulae (13) as follows:
$$\begin{aligned} \left\{ \begin{array}{llll} {\varvec{C}}_2{\varvec{V}}_0=0, &{} \\ \displaystyle {\varvec{C}}_2{\varvec{V}}_k= \frac{k!}{(k-1)!}({\varvec{I}}_W-{\varvec{B}}_1){\varvec{V}}_{k-1}-\sum _{l=2}^{k}\frac{k!}{(k-l)!}{\varvec{B}}_l{\varvec{V}}_{k-l}, &{} k=1,\cdots , W-2. \end{array} \right. \end{aligned}$$
Let
$$\begin{aligned} {\varvec{V}}_{k}=\left[ \begin{array}{cccccccccccccccc} V_{0,0}^{(k)} &{} V_{0,1}^{(k)} &{} \cdots &{} V_{0,m}^{(k)} \\ V_{1,0}^{(k)} &{} V_{1,1}^{(k)} &{} \cdots &{} V_{1,m}^{(k)} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ V_{m,0}^{(k)} &{} V_{m,1}^{(k)} &{} \cdots &{} V_{m,m}^{(k)} \\ \end{array} \right] \end{aligned}$$
where \(V_{i,l}^{(k)},\ 0\le l \le m\) are \(W_i\times W_0\) matrix. We have that
$$\begin{aligned} {\varvec{C}}_2{\varvec{V}}_k=\left[ \begin{array}{cccccccccccccccc} C_{20}V_{0,0}^{(k)} &{} C_{20}V_{0,1}^{(k)} &{} \cdots &{} C_{20}V_{0,m}^{(k)} \\ C_{21}V_{0,0}^{(k)} &{} C_{21}V_{0,1}^{(k)} &{} \cdots &{} C_{21}V_{0,m}^{(k)} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ C_{2m}V_{0,0}^{(k)} &{} V_{0,1}^{(k)} &{} \cdots &{} C_{2m}V_{0,m}^{(k)} \\ \end{array} \right] . \end{aligned}$$
The product matrix does not include the submatrices \(V_{il}^{(k)},\ 1\le i \le m; 0\le l \le m\). This means that they can be freely determined and only the submatrices \(V_{0,l}^{(k)}, 0\le l \le m\) of the first row of \(V_k\) need to be found. From (14), we can construct the following recursion algorithm for \(V_{0,l}^{(k)}, 0\le l \le m\).
Step 1. Determine \(V_{0,l}^{(0)}\) from the equations:
$$\begin{aligned} C_{2i}V_{0,l}^{(0)}=0, 0\le i,\ l\le m. \end{aligned}$$
Step 2. Determine \(V_{0,l}^{(1)}\) from the equations:
$$\begin{aligned} \left\{ \begin{array}{llll} C_{20}V_{0,l}^{(1)}=(I_{W_0}-D_{0}^{(1)})V_{0,l}^{(0)}-E_1^{(1)}V_{1,l}^{(0)} &{} 0\le l \le m \\ C_{2i}V_{0,l}^{(1)}=-D_i^{(1)}V_{0,l}^{(0)}+(I_{W_i}-F_{i}^{(1)})V_{i,l}^{(0)}-E_{i+1}^{(1)}V_{i+1,l}^{(0)} &{} \ 0\le l \le m; 1\le i \le m-1 \\ C_{2m}V_{0,l}^{(1)}=-D_m^{(1)}V_{0,l}^{(0)}+(I_{W_m}-F_m^{(1)})V_{m,l}^{(0)} &{} 0 \le l \le m. \end{array} \right. \end{aligned}$$
Step 3. Determine \(V_{0,l}^{(k)}\) for \(k=2,\cdots , W-2\) from the equations:
$$\begin{aligned} \left\{ \begin{array}{llllll} \displaystyle C_{20}V_{0,l}^{(k)}=\frac{k!}{(k-1)!}[(I_{W_0}-D_{0}^{(1)})V_{0,l}^{(k-1)}-E_1^{(1)}V_{1,l}^{(k-1)}] &{} \\ -\displaystyle \sum _{a=2}^{k}\frac{k!}{(k-a)!}[D_0^{(a)}V_{0,l}^{(k-a)}+E_1^{(a)}V_{1,l}^{(k-a)}],&{} 0\le l \le m \\ \displaystyle C_{2i}V_{0,l}^{(k)}=\frac{k!}{(k-1)!}[-D_{i}^{(1)}V_{0,l}^{(k-1)}+(I_{W_i}-F_i^{(1)})V_{i,l}^{(k-1)}-E_{i+1}^{(1)}V_{i+1,l}^{(k-1)}] &{} \\ -\displaystyle \sum _{a=2}^{k}\frac{k!}{(k-a)!}[D_i^{(a)}V_{0,l}^{(k-a)}+F_{i}^{(a)}V_{i,l}^{(k-a)}+E_{i+1}^{(a)}V_{i+1,l}^{(k-a)}], &{} 0\le l \le m;\\ &{} 1\le i \le m \\ \displaystyle C_{2m}V_{0,l}^{(k)}=\frac{k!}{(k-1)!}[-D_{m}^{(1)}V_{0,l}^{(k-1)}+(I_{W_m}-F_m^{(1)})V_{m,l}^{(k-1)}] &{} \\ -\displaystyle \sum _{a=2}^{k}\frac{k!}{(k-a)!}[D_m^{(a)}V_{0,l}^{(k-a)}+F_m^{(a)}V_{m,l}^{(k-a)}], &{} 0\le l \le m. \end{array} \right. \end{aligned}$$