Abstract
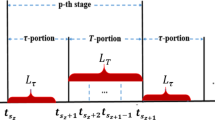
This paper concerns the stability of a one-dimensional Euler-Bernoulli beam equation with external disturbance and output feedback time-delay, in which the disturbance is bounded by an exponential function. In order to estimate disturbance, the authors design an estimator of disturbance, which is composed of two parts: One is the system measurement that is called the eigen-measurement, another is a time-variant estimator of disturbance. Thus, the feedback controller which is based on the estimate of the disturbance is designed to stabilize the system. The finite-time stability of the system under this control law is proved by Lyapunov function method. Finally, some numerical simulations on the dynamical behavior of the closed-loop system is presented to show the correctness of the result.
Similar content being viewed by others
References
Guo B Z and Yang Y K, Dynamic stabilization of an Euler-Bernoulli beam equation with time delay in boundary observation, Automatica, 2009, 45: 1468–1475.
Xu G Q, Yung S P, and Li L K, Stabilization of wave systems with input delay in the boundary control, ESAIM Contr. Optim. CA, 2006, 12: 770–785.
Nicaise S and Pignotti C, Stability and instability results of the wave equation with a delay term in the boundary or internal feedbacks, SIAM J. Contrl. Optim., 2006, 45(5): 1561–1585.
Nicaise S and Valein J, Stabilization of the wave equation on 1-d networks with a delay term in the nodal feedbacks, NETW. Heterog. Media, 2007, 2(3): 425–479.
Benhassi E M A, Ammari K, Boulite S, et al., Feedback stabilization of a class of evolution equations with delay, J. Evol. Equ., 2009, 9: 103–121.
Said-Houari B and Laskri Y, A stability result of a Timoshenko system with a delay term in the internal feedback, Appl. Math. Comput., 2010, 217: 2857–2869.
Shang Y F, Xu G Q, and Chen Y L, Stability analysis of Euler-Bernoulli beam with input delay in the boundary control, Asian J. Control, 2012, 14: 1–11.
Shang Y F and Xu G Q, Stabilization of Euler-Bernoulli beam with input delay in the boundary control, Syst. Control Lett., 2012, 61: 1069–1078.
Guo B Z and Jin F F, Output feedback stabilization for one-dimensional wave equation subject to boundary disturbance, IEEE Trans. Automat. Control, 2015, 60(3): 824–830.
He W and Ge S S, Cooperative control of a nonuniform gantry crane with constrained tension, Automatica, 2016, 66: 146–154.
He W and Ge S S, Vibration control of a flexible beam with output constraint, IEEE Trans. Ind. Electron, 2015, 24: 427–436.
He W and Zhang S, Control design for nonlinear flexible wings of a robotic aircraft, IEEE Trans. Conrol Syst. Technol, 2017, 25(1): 351–357.
He W, Zhang S, and Ge S S, Adaptive control of a flexible crane system with the boundary output constraint, IEEE Trans Ind. Electron, 2014, 61(8): 4126–4133.
Liu D, Chen Y, and Xu G Q, Stabilization of Timoshenko beam using disturbance observer-based boundary controls, The Chinese Control Conference, 2016, 35: 1296–1300.
Guo W and Guo B Z, Adaptive output feedback stabilization for one-dimensional wave equation with corrupted observation by harmonic disturbance, SIAM J. Control Optim., 2015, 51: 1679–1706.
Guo B Z and Zhou H C, Active disturbance rejection control for rejecting boundary disturbance from multidimensional Kirchho plate via boundary control, SIAM J. Control Optim., 2014, 52: 2800–2830.
Guo B Z and Zhou H C, The active disturbance rejection control to stabilization for multidimensional wave equation with boundary controlmatched disturbance, IEEE Trans. Automat. Control, 2015, 60: 143–157.
Wang L, Shang Y F, Han Z J, et al., Exponential stabilization of thermoelastic system of type II with non-uniform bounded disturbance, Applicable Analysis, 2016, 54: 775–793.
Li Y F and Xu G Q, Stabilization of an Euler-Bernoulli beam system with a tip mass subject to uniform bounded disturbance, IMA J. Math. Control Inf., 2016, 21: 1093–1111.
Pisano A and Orlov Y, Boundary second-order sliding-mode control of an uncertain heat process with unbounded matched perturbation, Automatica, 2012, 48(8): 1768–1775.
Guo B Z and Jin F F, The active disturbance rejection and sliding mode control approach to the stabilization of the Euler-Bernoulli beam equation with boundary input disturbance, Automatica, 2013, 49: 2911–2918.
Guo B Z and Jin F F, Sliding mode and active disturbance rejection control to stabilization of one-dimensional anti-stable wave equations subject to disturbance in boundary input, IEEE Trans. Automat. Control, 2013, 58: 1269–1274.
Shang Y F and Xu G Q, Dynamic control of an Euler-Bernoulli equation with time-delay and disturbance in the boundary control. Int J. Control, 2017, 7: 31–25.
Nicaise S and Pignotti C, Stability instability results of the wave equation with a delay term in the boundary or internal feedbacks, SIAM J. Control Optim., 2006, 45: 1561–1585.
Xu G Q and Guo B Z, Riesz basis property of evolution equations in Hilbert spaces and application to a coupled string equation, SIAM J. Control Optim., 2003, 42: 571–591.
Adams R A, Sobolev space, Bulletin of the American Mathematical Society, 1976, 82: 668–673
Pazy A, Semigroup of Linear Operator and Applications to Partial Differential Equations, Springer-Verlag, New York, 1983.
Author information
Authors and Affiliations
Corresponding authors
Additional information
This research was supported by the National Science Natural Foundation in China under Grant No. 61773277.
This paper was recommended for publication by Editor SUN Jian.
Rights and permissions
About this article
Cite this article
Wu, J., Shang, Y. Exponential Stability of the Euler-Bernoulli Beam Equation with External Disturbance and Output Feedback Time-Delay. J Syst Sci Complex 32, 542–556 (2019). https://doi.org/10.1007/s11424-018-7182-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-018-7182-0