Structural biology response of a collagen hydrogel synthetic extracellular matrix with embedded human fibroblast: computational and experimental analysis

Abstract

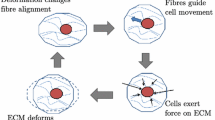
Adherent cells exert contractile forces which play an important role in the spatial organization of the extracellular matrix (ECM). Due to these forces, the substrate experiments a volume reduction leading to a characteristic shape. ECM contraction is a key process in many biological processes such as embryogenesis, morphogenesis and wound healing. However, little is known about the specific parameters that control this process. With this aim, we present a 3D computational model able to predict the contraction process of a hydrogel matrix due to cell–substrate mechanical interaction. It considers cell-generated forces, substrate deformation, ECM density, cellular migration and proliferation. The model also predicts the cellular spatial distribution and concentration needed to reproduce the contraction process and confirms the minimum value of cellular concentration necessary to initiate the process observed experimentally. The obtained continuum formulation has been implemented in a finite element framework. In parallel, in vitro experiments have been performed to obtain the main model parameters and to validate it. The results demonstrate that cellular forces, migration and proliferation are acting simultaneously to display the ECM contraction.

Appendix: Weak formulation

1.1 Discretization and nonlinear equations system

For the temporal discretization of the governing equations set, we consider the partition $\mathop \cup \nolimits_{n = 1}^{{n_{\text{step}} - 1}} [t_{n} , t_{n + 1} ]$ of the time interval of interest T and focus on the typical time subinterval $[t_{n} , t_{n + 1} ]$ with $\Delta t = t_{n + 1} - t_{n} \ge 0$ denoting the corresponding increment of time. It is assumed that the primary unknowns and all derivable quantities are known at time t _n . The generalized trapezoidal method is applied [20]. It is defined by $\alpha \in \left( {0,1} \right]$, such that $t_{n + \alpha } = t_{n} + \alpha \Delta t$. In this method, the following scheme is used for the temporal discretization of primary variables (only it is shown for c; ρ and u have the same discretization):

$$c_{n + 1} = c_{n} + \Delta t \dot{c}_{n + \alpha } ,$$

(17)

$$\dot{c}_{n + \alpha } = {c}_{n} \left( {1 - \alpha } \right) + \dot{c}_{n + 1} \alpha ,$$

(18)

where $c_{n + 1}$, $\dot{c}_{n + \alpha }$ and $\dot{c}_{n + 1}$ are approximations of $c(t_{n + 1} )$, $\left( {\frac{\partial c}{\partial t}} \right)(t_{n + \alpha } )$ and $\left( {\frac{\partial c}{\partial t}} \right)(t_{n + 1} )$, respectively. From a practical standpoint, $\tilde{c}_{n + 1}$ is introduced as a predictor value of $c_{n + 1}$, which only depends on magnitudes at time t _n :

$$\tilde{c}_{n + 1} = c_{n} + \left( {1 - \alpha } \right)\Delta t \cdot {c}_{n} ,$$

(19)

$\dot{c}_{n + 1}$ can be computed by

$$\dot{c}_{n + 1} = \frac{{c_{n + 1} - \tilde{c}_{n + 1} }}{\alpha \Delta t},$$

(20)

Substitution of Eqs. (19) and (20) in the weak form of the problem given by Eq. 16 yields to a semi-discrete set of equations that are discretized in time.

1.2 Spatial discretization of the problem

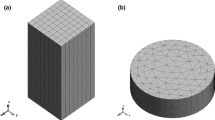
The semi-discrete system is discretized in space using the finite element method. The domain $\Omega$ is discretized into $n_{\text{el}}$ elements $\Omega^{e}$, with $\Omega = \mathop \cup \nolimits_{e = 1}^{{n_{\text{el}} }} \Omega^{e}$. The primary unknown fields are interpolated within a generic element $\Omega^{e}$ in terms of the nodal values through shape functions, that is,

$$\begin{aligned} \varvec{c}^{h} |_{{\Omega^{e} }} = {\mathbf{N}}_{c} \cdot {\mathbf{c}}^{e} , \hfill \\ \rho^{h} |_{{\Omega^{e} }} = {\mathbf{N}}_{\rho } \cdot {\varvec{\rho}}^{e} , \hfill \\ {\mathbf{u}}^{h} |_{{\Omega^{e} }} = {\mathbf{N}}_{{\mathbf{u}}} \cdot {\mathbf{u}}^{e} . \hfill \\ \end{aligned}$$

(21)

where ${\mathbf{c}}^{e}$, ${\varvec{\rho}}^{e}$ and ${\mathbf{u}}^{e}$ are column vectors of nodal values of the primary unknowns at element e and ${\mathbf{N}}_{c}$, ${\mathbf{N}}_{\rho }$ and ${\mathbf{N}}_{{\mathbf{u}}}$ are matrices of element shape functions, that is,

$$\begin{aligned} {\mathbf{N}}_{c} & = [N_{c}^{1} , \ldots ,N_{c}^{{n_{\text{en}} }} ], \\ {\mathbf{N}}_{\rho } & = [N_{\rho }^{1} , \ldots ,N_{\rho }^{{n_{\text{en}} }} ], \\ {\mathbf{N}}_{{\mathbf{u}}} & = \left[ {\begin{array}{*{20}c} {N_{u}^{1} } & 0 & 0 \\ 0 & {N_{u}^{1} } & 0 \\ 0 & 0 & {N_{u}^{1} } \\ \end{array} } \right] \cdots \left[ {\begin{array}{*{20}c} {N_{u}^{{n_{\text{en}} }} } & 0 & 0 \\ 0 & {N_{u}^{{n_{\text{en}} }} } & 0 \\ 0 & 0 & {N_{u}^{{n_{\text{en}} }} } \\ \end{array} } \right], \\ \end{aligned}$$

(22)

where N ⁱ is the shape function associated to element node i and $n_{\text{en}}$ the number of element nodes. Following a Bubnov–Galerkin scheme, the same shape functions are also applied to interpolate the test functions:

$$\begin{aligned} \delta c^{h} |_{{\Omega^{e} }} & = {\mathbf{N}}_{c} \cdot \delta c^{e} , \\ \delta \rho^{h} |_{{\Omega^{e} }} & = {\mathbf{N}}_{\rho } \cdot \delta \rho^{e} , \\ \delta {\mathbf{u}}^{h} |_{{\Omega^{e} }} & = {\mathbf{N}}_{u} \cdot \delta {\mathbf{u}}^{e} . \\ \end{aligned}$$

(23)

Likewise, the discretization of the related gradients of the test functions and the primary unknowns take the following element-wise format:

$$\nabla c^{h} |_{{\Omega^{e} }} = \nabla \cdot {\mathbf{N}}_{c} {\mathbf{c}}^{e} \mathop { \to} \limits^{\text{yields}} \nabla \delta c_{h} |_{{\Omega^{e} }} = \nabla \cdot {\mathbf{N}}_{c} \delta {\mathbf{c}}^{e} ,$$

(24)

$$\nabla \rho^{h} |_{{\Omega^{e} }} = \nabla \cdot {\mathbf{N}}_{\rho } {\varvec{\rho}}^{e} \mathop {\to} \limits^{\text{yields}} \nabla \delta \rho_{h} |_{{\Omega^{e} }} = \nabla \cdot {\mathbf{N}}_{\rho } \delta {\varvec{\rho}}^{e} .$$

(25)

The strains are interpolated in the following form:

$$\varepsilon^{h} |_{{\Omega^{e} }} = {\mathbf{B}}_{{\mathbf{u}}} {\mathbf{u}}_{e} ,$$

(26)

where ${\mathbf{B}}_{{\mathbf{u}}}$ is a matrix of derivatives of shape functions:

$${\mathbf{B}}_{{\mathbf{u}}} = {\mathbf{HN}}_{{\mathbf{u}}} ,$$

(27)

$${\mathbf{H}} = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial x}} & 0 & 0 \\ 0 & {\frac{\partial }{\partial y}} & 0 \\ 0 & 0 & {\frac{\partial }{\partial z}} \\ {\frac{1}{2}\frac{\partial }{\partial y}} & {\frac{1}{2}\frac{\partial }{\partial x}} & 0 \\ {\frac{1}{2}\frac{\partial }{\partial y}} & 0 & {\frac{1}{2}\frac{\partial }{\partial y}} \\ 0 & {\frac{1}{2}\frac{\partial }{\partial z}} & {\frac{1}{2}\frac{\partial }{\partial y}} \\ \end{array} } \right].$$

(28)

Substituting the Eqs. (21), (23) and (27) into the semi-discrete system and choosing appropriately the arbitrary coefficients ${\delta }{\mathbf{c}}^{e}$, ${\delta }{\varvec{\rho}}^{e}$ and ${\delta }{\mathbf{u}}^{e}$ of the test functions, one can finally arrive to a set of nonlinear algebraic equations which is sufficient to determine the nodal values of the primary unknowns and can be written in the form:

$${\mathbf{F}}^{\text{int}} = \left( {{\mathbb{Z}}_{n + 1} ,\frac{{{\mathbb{Z}}_{n + 1} - \tilde{\mathbb{Z}}_{n + 1} }}{\alpha \Delta t}} \right) = {\mathbf{F}}^{\text{ext}} \left( {{\mathbb{Z}}_{n + 1} } \right) ,$$

(29)

where ${\mathbb{Z}}_{n + 1}$ and ${\tilde{\mathbb{Z}}}_{n + 1}$ are the global column vector of nodal values of the primary unknown fields at time $t_{n + 1}$ and the corresponding predictor value, respectively. This vector can be obtained as follows:

$${\mathbb{Z}}_{n + 1} = {\mathcal{R}}_{e = 1}^{{n_{\text{en}} }} {\mathbf{d}}_{n + 1}^{e} ,$$

(30)

$${\tilde{\mathbb{Z}}}_{n + 1} = {\mathcal{R}}_{e = 1}^{{n_{\text{en}} }} {\tilde{\mathbf{d}}}_{n + 1}^{e} ,$$

(31)

where ${\mathcal{R}}$ denotes the standard finite element assembly operator and ${\mathbf{d}}_{n + 1}^{e}$ and ${\tilde{\mathbf{d}}}_{n + 1}^{e}$ can be defined by

$${\mathbf{d}}_{n + 1}^{e} = [{\mathbf{c}}_{n + 1}^{e} ,{\varvec{\rho}}_{n + 1}^{e} ,{\mathbf{u}}_{n + 1}^{e} ]^{\text{T}} ,$$

(32)

$${\tilde{\mathbf{d}}}_{n + 1}^{e} = [{\tilde{\mathbf{c}}}_{n + 1}^{e} ,{\tilde{\varvec{\rho }}}_{n + 1}^{e} ,{\tilde{\mathbf{u}}}_{n + 1}^{e} ]^{\text{T}} .$$

(33)

The internal and external global force vector represented by ${\mathbf{F}}^{\text{int}}$ and ${\mathbf{F}}^{\text{ext}}$ also come from the assembly of element contributions:

$$F_{n + 1}^{\text{int}} = {\mathcal{R}}_{e = 1}^{{n_{\text{en}} }} {\mathbf{f}}_{n + 1}^{{{\text{int}},e}} ,$$

(34)

$$F_{n + 1}^{\text{ext}} = {\mathcal{R}}_{e = 1}^{{n_{\text{en}} }} {\mathbf{f}}_{n + 1}^{{{\text{ext}},e}} ,$$

(35)

where

$${\mathbf{f}}_{n + 1}^{{{\text{int}},e}} = [{\mathbf{f}}_{c,n + 1}^{{{\text{int}},e}} ,{\mathbf{f}}_{\rho ,n + 1}^{{{\text{int}},e}} ,{\mathbf{f}}_{{{\mathbf{u}},n + 1}}^{{{\text{int}},e}} ]^{\text{T}} ,$$

(36)

$${\mathbf{f}}_{n + 1}^{{{\text{ext}},e}} = [{\mathbf{f}}_{c,n + 1}^{{{\text{ext}},e}} ,{\mathbf{f}}_{\rho ,n + 1}^{{{\text{ext}},e}} ,{\mathbf{f}}_{{{\mathbf{u}},n + 1}}^{{{\text{ext}},e}} ]^{\text{T}} .$$

(37)

The element contributions to the internal force can read as:

$$\begin{aligned} {\mathbf{f}}_{c,n + 1}^{{{\text{int}},e}} & = \mathop \int \nolimits {\mathbf{N}}_{c}^{\text{T}} \frac{{c_{n + 1}^{h} - \tilde{c}_{n + 1}^{h} }}{\alpha \Delta t}{\text{d}}V + \mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{c}^{\text{T}} [D\nabla c^{h} - c^{h} \frac{{{\mathbf{u}}_{n + 1}^{h} - {\tilde{\mathbf{u}}}_{n + 1}^{h} }}{\alpha \Delta t} - h\nabla \rho^{h} ]_{n + 1} {\text{d}}V, \\ {\mathbf{f}}_{\rho ,n + 1}^{{{\text{int}},e}} & = \mathop \int \nolimits {\mathbf{N}}_{\rho }^{\text{T}} \frac{{\rho_{n + 1}^{h} - \tilde{\rho }_{n + 1}^{h} }}{\alpha \Delta t}{\text{d}}V + \mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{\rho }^{\text{T}} \rho_{n + 1}^{h} \frac{{{\mathbf{u}}_{n + 1}^{h} - {\tilde{\mathbf{u}}}_{n + 1}^{h} }}{\alpha \Delta t}{\text{d}}V, \\ {\mathbf{f}}_{{{\mathbf{u}},n + 1}}^{{{\text{int}},e}} & = \mathop \int \nolimits {\mathbf{B}}_{\text{u}}^{\text{T}} [{\mathbf{D}}_{\text{elas}} {\mathbf{Hu}}^{h} + {\mathbf{D}}_{\text{visc}} {\mathbf{H}}\frac{{{\mathbf{u}}_{n + 1}^{h} - {\tilde{\mathbf{u}}}_{n + 1}^{h} }}{\alpha \Delta t} + \frac{{P_{\text{cell}} c^{h} }}{{1 + \lambda c^{h} }}{\mathbf{I}}]_{n + 1} {\text{d}}V, \\ \end{aligned} ,$$

(38)

where ${\mathbf{D}}_{\text{elas}}$ and ${\mathbf{D}}_{\text{visc}}$ are the mechanical behavior matrices:

$${\mathbf{D}}_{\text{elas}} = \xi \left[ {\begin{array}{*{20}c} {1 - \nu } & \nu & \nu & {} & {} & {} \\ \nu & {1 - \nu } & \nu & {} & {\tilde{0}} & {} \\ \nu & \nu & {1 - \nu } & {} & {} & {} \\ {} & {} & {} & {\frac{1 - 2\nu }{2}} & 0 & 0 \\ {} & {\tilde{0}} & {} & 0 & {\frac{1 - 2\nu }{2}} & 0 \\ {} & {} & {} & 0 & 0 & {\frac{1 - 2\nu }{2}} \\ \end{array} } \right],$$

(39)

where $\xi = \frac{E}{(1 + \nu )(1 - 2\nu )}$ and

$${\mathbf{D}}_{visc} = \left[ {\begin{array}{*{20}c} {\mu_{1} + \mu_{2} } & {\mu_{2} } & {\mu_{2} } & {} & {} & {} \\ {\mu_{2} } & {\mu_{1} + \mu_{2} } & {\mu_{2} } & {} & {\tilde{0}} & {} \\ {\mu_{2} } & {\mu_{2} } & {\mu_{1} + \mu_{2} } & {} & {} & {} \\ {} & {} & {} & {\mu_{1} } & 0 & 0 \\ {} & {\tilde{0}} & {} & 0 & {\mu_{1} } & 0 \\ {} & {} & {} & 0 & 0 & {\mu_{1} } \\ \end{array} } \right].$$

(40)

In the case of the external force vector, the element contributions have the following expressions:

$$\begin{aligned} {\mathbf{f}}_{c,n + 1}^{{{\text{ext}},e}} & = \mathop \int \nolimits {\mathbf{N}}_{c}^{\text{T}} rc_{n + 1}^{h} {\text{d}}V , \\ {\mathbf{f}}_{\rho ,n + 1}^{{{\text{ext}},e}} & = \mathbf{0} , \\ {\mathbf{f}}_{{{\mathbf{u}},n + 1}}^{{{\text{ext}},e}} & = \mathop \int \nolimits {\mathbf{N}}_{{\mathbf{u}}}^{\text{T}} \rho_{n + 1}^{h} {\mathbf{f}}_{n + 1}^{\text{ext}} {\text{d}}V . \\ \end{aligned}$$

(41)

1.3 Linearization of the problem

The solution of the set equation system 41 is obtained by a standard Newton–Raphson iterative solution procedure. The components of the internal and external global tangent matrices can be defined as the following

$$\begin{aligned} {\mathbf{K}}_{cc,n + 1}^{{{\text{int,}}e}} & = \frac{1}{\alpha \Delta t}\mathop \int \nolimits {\mathbf{N}}_{c}^{\text{T}} \cdot {\mathbf{N}}_{c} {\text{d}}V + \mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{c}^{\text{T}} D\nabla \cdot {\mathbf{N}}_{c} {\text{d}}V - \mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{c}^{\text{T}} \frac{{{\mathbf{u}}_{n + 1}^{h} - {\tilde{\mathbf{u}}}_{n + 1}^{h} }}{\alpha \Delta t}{\mathbf{N}}_{c} {\text{d}}V, \\ {\mathbf{K}}_{{c{\mathbf{u}},n + 1}}^{{{\text{int}},e}} & = - \frac{1}{\alpha \Delta t}\mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{c}^{\text{T}} c_{n + 1}^{h} {\mathbf{N}}_{{\mathbf{u}}} {\text{d}}V, \\ {\mathbf{K}}_{\rho \rho ,n + 1}^{{{\text{int}},e}} & = - \frac{1}{\alpha \Delta t}\mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{\rho }^{\text{T}} {\mathbf{N}}_{\rho } {\text{d}}V - \mathop \int \nolimits \nabla \cdot {\mathbf{N}}_{\rho }^{\text{T}} \frac{{{\mathbf{u}}_{n + 1}^{h} - {\tilde{\mathbf{u}}}_{n + 1}^{h} }}{\alpha \Delta t}{\mathbf{N}}_{\rho } {\text{d}}V, \\ {\mathbf{K}}_{{{\mathbf{uu}},n + 1}}^{{{\text{int}},e}} & = \mathop \int \nolimits {\mathbf{B}}_{{\mathbf{u}}}^{\text{T}} {\mathbf{D}}_{\text{elas}} {\mathbf{B}}_{{\mathbf{u}}} {\text{d}}V + \frac{1}{\alpha \Delta t}\mathop \int \nolimits {\mathbf{B}}_{{\mathbf{u}}}^{\text{T}} {\mathbf{D}}_{visc} {\mathbf{B}}_{{\mathbf{u}}} {\text{d}}V + \mathop \int \nolimits {\mathbf{B}}_{{\mathbf{u}}}^{\text{T}} \frac{{P_{\text{cell}} c_{n + 1}^{h} }}{{1 + \lambda c_{n + 1}^{h} }}{\mathbf{I}}\nabla \cdot {\mathbf{N}}_{{\mathbf{u}}} {\text{d}}V, \\ {\mathbf{K}}_{{{\mathbf{u}}c,n + 1}}^{{{\text{int}},e}} & = \mathop \int \nolimits {\mathbf{B}}_{{\mathbf{u}}}^{\text{T}} \frac{{P_{\text{cell}} }}{{1 + \lambda c_{n + 1}^{h} }} {\mathbf{I}}\nabla \cdot {\mathbf{N}}_{c} {\text{d}}V, \\ {\mathbf{K}}_{{{\mathbf{u}}c,n + 1}}^{{{\text{ext}},e}} & = \mathop \int \nolimits {\mathbf{N}}_{{\mathbf{u}}}^{\text{T}} r {\mathbf{N}}_{c} {\text{d}}V, \\ {\mathbf{K}}_{{{\mathbf{uu}},n + 1}}^{{{\text{ext}},e}} & = - \mathop \int \nolimits {\mathbf{N}}_{{\mathbf{u}}}^{\text{T}} \rho_{n + 1}^{h} {\mathbf{N}}_{{\mathbf{u}}} {\text{d}}V, \\ {\mathbf{K}}_{{{\mathbf{u}}\rho ,n + 1}}^{{{\text{ext}},e}} & = - \mathop \int \nolimits {\mathbf{N}}_{{\mathbf{u}}}^{\text{T}} {\mathbf{u}} {\mathbf{N}}_{\varvec{\rho}} {\text{d}}V. \\ \end{aligned}$$

(42)