Fast approximation for joint optimization of segmentation, shape, and location priors, and its application in gallbladder segmentation

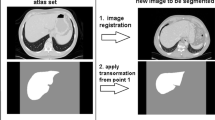
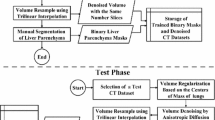
Abstract

Purpose

This paper addresses joint optimization for segmentation and shape priors, including translation, to overcome inter-subject variability in the location of an organ. Because a simple extension of the previous exact optimization method is too computationally complex, we propose a fast approximation for optimization. The effectiveness of the proposed approximation is validated in the context of gallbladder segmentation from a non-contrast computed tomography (CT) volume.

Methods

After spatial standardization and estimation of the posterior probability of the target organ, simultaneous optimization of the segmentation, shape, and location priors is performed using a branch-and-bound method. Fast approximation is achieved by combining sampling in the eigenshape space to reduce the number of shape priors and an efficient computational technique for evaluating the lower bound.

Results

Performance was evaluated using threefold cross-validation of 27 CT volumes. Optimization in terms of translation of the shape prior significantly improved segmentation performance. The proposed method achieved a result of 0.623 on the Jaccard index in gallbladder segmentation, which is comparable to that of state-of-the-art methods. The computational efficiency of the algorithm is confirmed to be good enough to allow execution on a personal computer.

Conclusions

Joint optimization of the segmentation, shape, and location priors was proposed, and it proved to be effective in gallbladder segmentation with high computational efficiency.

Appendix

The lower bound defined in Eq. (12) satisfies the three properties required for the branch-and-bound method.

Monotonicity :

The inequality $\textit{LB}(\varTheta _\textit{ch}) \ge \textit{LB}(\varTheta )$ holds for any nested domains $\varTheta _\textit{ch}\subset \varTheta$. See Corollary 1 with the proof below.

Tightness :

The bound is tight for a singleton node, i.e., $\textit{LB}(\{\varvec{\theta }\}) = f(\varvec{\theta })$ is satisfied for any $\varvec{\theta }\in \mathbb {R}^d\times \mathbb {Z}^3$.

Computability :

Evaluation of the lower bound in Eq. (12) $\varTheta =S\times T$ requires taking the minimum of $F^i(\varvec{\theta })$ and $B^i(\varvec{\theta })$ in terms of $\varvec{\theta }\in \varTheta$, and operation in terms of $\varvec{\theta }\in \varTheta$, as well as taking the outer minimum in terms of $\mathbf {x}\in \mathcal {L}^N$. As described in the section “calculation of the lower bound”, the computational complexity of the former minimum operation over $\varvec{\theta }\in \varTheta$ is $O(dN+ \log |T|)$. The latter minimum operation equals the minimization of a submodular quadratic pseudo-Boolean function. Theoretical complexity is the low-order polynomial of $N$ time, if it is solved using s–t mincut [12]. Therefore, computability is satisfied in our study.

Corollary 1

For any nested domains $\varTheta _\textit{ch}\subset \varTheta$, the inequality $\textit{LB}(\varTheta _\textit{ch}) \ge \textit{LB}(\varTheta )$ holds.

Proof

Let us denote $A(\mathbf {x}, \varTheta )$ as the expression within the outer minimum of Eq. (12), i.e.,

$$\begin{aligned} A(\mathbf {x}, \varTheta )= & {} \sum _{i\in \mathcal {V}}{\left( \min _{\varvec{\theta }\in \varTheta }{F^i(\varvec{\theta })} \cdot x_i+ \min _{\varvec{\theta }\in \varTheta }{B^i(\varvec{\theta })} \cdot (1 - x_i) \right) }\nonumber \\&+ \sum _{(i,j)\in \mathcal {E}}{ P^{ij} \cdot \left| x_i- x_j\right| }. \end{aligned}$$

(24)

Assume $\varTheta _\textit{ch}\subset \varTheta$. Then, for any fixed $\mathbf {x}$, for all pixels $i\in \mathcal {V}$, the following inequalities hold:

$$\begin{aligned} \min _{\varvec{\theta }\in \varTheta _\textit{ch}}{F^i(\varvec{\theta })} \cdot x_i\ge & {} \min _{\varvec{\theta }\in \varTheta }{F^i(\varvec{\theta })} \cdot x_i\end{aligned}$$

(25)

$$\begin{aligned} \min _{\varvec{\theta }\in \varTheta _\textit{ch} }{B^i(\varvec{\theta })} \cdot (1 - x_i)\ge & {} \min _{\varvec{\theta }\in \varTheta }{B^i(\varvec{\theta })} \cdot (1 - x_i) \end{aligned}$$

(26)

This is because $\varTheta _\textit{ch}$ is a subset of $\varTheta$ and $x_i$, and $(1-x_i)$ are nonnegative ($\because x_i\in \{0, 1\}$). By summing the inequalities Eqs. (25) and (26) over all pixels ($i\in \mathcal {V}$), and adding $\sum _{(i,j)\in \mathcal {E}}{P^{ij} \cdot \left| x_i- x_j\right| }$ to both sides, which are constant with respect to $\varvec{\theta }$, we obtain

$$\begin{aligned} A(\mathbf {x}, \varTheta _\textit{ch}) \ge A(\mathbf {x}, \varTheta ) \quad \forall \mathbf {x}\in \mathcal {L}^N, \end{aligned}$$

(27)

i.e., monotonicity holds for any constant value of $\mathbf {x}$. We define $\mathbf {x}^*_\textit{ch}$ and $\mathbf {x}^*$ as the segmentation labels obtained by $\mathbf {x}^*_\textit{ch} = \mathop {\mathrm{arg~ min}}\limits _{\mathbf {x}\in \mathcal {L}^N}A(\mathbf {x}, \varTheta _\textit{ch})$ and $\mathbf {x}^* = \mathop {\mathrm{arg~ min}}\limits _{\mathbf {x}\in \mathcal {L}^N}A(\mathbf {x}, \varTheta )$, respectively. Then, from the monotonicity in Eq. (27) and the definition of $\mathbf {x}^*$, we obtain

$$\begin{aligned}&\textit{LB}(\varTheta _\textit{ch}) = A(\mathbf {x}^*_\textit{ch},\varTheta _\textit{ch})\nonumber \\&\quad \mathop {\ge }\limits ^{\because {(27)}} A(\mathbf {x}^*_\textit{ch},\varTheta ) \mathop {\ge }\limits ^{\because \text {def}} A(\mathbf {x}^*,\varTheta ) = \textit{LB}(\varTheta ). \end{aligned}$$

(28)

$\square$