Performance of convex underestimators in a branch-and-bound framework

Abstract

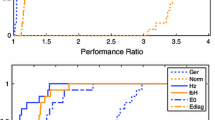
The efficient determination of tight lower bounds in a branch-and-bound algorithm is crucial for the global optimization of models spanning numerous applications and fields. The global optimization method $\alpha$-branch-and-bound ($\alpha$BB, Adjiman et al. in Comput Chem Eng 22(9):1159–1179, 1998b, Comput Chem Eng 22(9):1137–1158, 1998a; Adjiman and Floudas in J Global Optim 9(1):23–40, 1996; Androulakis et al. J Global Optim 7(4):337–363, 1995; Floudas in Deterministic Global Optimization: Theory, Methods and Applications, vol. 37. Springer, Berlin, 2000; Maranas and Floudas in J Chem Phys 97(10):7667–7678, 1992, J Chem Phys 100(2):1247–1261, 1994a, J Global Optim 4(2):135–170, 1994), guarantees a global optimum with $\epsilon$-convergence for any $\mathcal {C}^2$-continuous function within a finite number of iterations via fathoming nodes of a branch-and-bound tree. We explored the performance of the $\alpha$BB method and a number of competing methods designed to provide tight, convex underestimators, including the piecewise (Meyer and Floudas in J Global Optim 32(2):221–258, 2005), generalized (Akrotirianakis and Floudas in J Global Optim 30(4):367–390, 2004a, J Global Optim 29(3):249–264, 2004b), and nondiagonal (Skjäl et al. in J Optim Theory Appl 154(2):462–490, 2012) $\alpha$BB methods, the Brauer and Rohn+E (Skjäl et al. in J Global Optim 58(3):411–427, 2014) $\alpha$BB methods, and the moment method (Lasserre and Thanh in J Global Optim 56(1):1–25, 2013). Using a test suite of 40 multivariate, box-constrained, nonconvex functions, the methods were compared based on the tightness of generated underestimators and the efficiency of convergence of a branch-and-bound global optimization algorithm.