Skip to main content
SpringerLink
Log in

Properties of subgradient projection iteration when applying to linear imaging system

  • Original paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

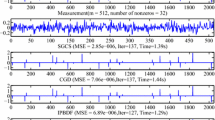
In this paper, the subgradient projection iteration is used to find an approximation solution of a weighted least-squares problem with respect to linear imaging system. Instead of an exact or approximate line search in each iteration, the step length in this paper is fixed by the weighted least-square function and the current iteration. Using weighted singular value decomposition, we estimate the bounds of step length. Consequently, we provide the decreasing property and the sufficient condition for convergence of the iterative algorithm. Furthermore, we perform a numerical experiment on a two dimensional image reconstruction problem to confirm the validity of this subgradient projection iteration.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Herman, G.T.: Image Reconstruction from Projections: The Fundamentals of Computerized Tomography. Academic Press, New York (1980)

    MATH  Google Scholar 

  2. Natterer, F., Wubbeling, F.: Mathematical Methods in Image Reconstruction. Society for Industrial and Applied Mathematics, Philadelphia (2001)

    Book  MATH  Google Scholar 

  3. Censor, Y., Herman, G.T.: On some optimization techniques in image reconstruction from projections. Appl. Numer. Math. 3(5), 365–391 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  4. Olver, P.J., Shakiban, C.: Applied Linear Algebra. Prentice-Hall, Upper Saddle River (2006)

    MATH  Google Scholar 

  5. Golub, G.G., Van Loan, C.F.: Matrix Computations, 4th edn. The Johns Hopkins University Press, Baltimore (2013)

    MATH  Google Scholar 

  6. Jiang, M., Wang, G.: Convergence studies on iterative algorithms for image reconstruction. IEEE Trans. Med. Imaging 22(5), 569–579 (2003)

    Article  Google Scholar 

  7. Qu, G., Wang, C., Jiang, M.: Necessary and sufficient convergence conditions for algebraic image reconstruction algorithms. IEEE Trans. Image Process. 18(2), 435–440 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Wang, M., Polydorides, N., Bertsekas, D.P.: Approximate simulation-based solution of large-scale least squares problems. Lab. for Information and Decision Systems Report LIDS-P-2819, MIT (2009)

  9. Balabdaoui, F., Rufibach, K., Santambrogio, F.: Least-squares estimation of two-ordered monotone regression curves. J. Nonparametric Stat. 22(8), 1019–1037 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. Freund, R.M., Grigas, P., Mazumder, R.: A new perspective on boosting in linear regression via subgradient optimization and relatives. Ann. Stat. 45(6), 2328–2364 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. Yu, H., Bertsekas, D.P.: Convergence results for some temporal difference methods based on least squares. IEEE Trans. Autom. Control 54(7), 1515–1531 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Kiwiel, K.C.: Convergence of approximate and incremental subgradient methods for convex optimization. SIAM J. Optim. 14(3), 807–840 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Dang, Y., Gao, Y.: A new simultaneous subgradient projection algorithm for solving a multiple-sets split feasibility problem. Appl. Math. 59(1), 37–51 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  14. Gondzio, J., Vial, J.P.: Warm start and \(\varepsilon \)-subgradients in a cutting plane scheme for block-angular linear programs. Comput. Optim. Appl. 14(1), 17–36 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  15. Vershinin, Y.N., Bykov, A.A., Krutikov, V.N., Meshechkin, V.V.: On the subgradient method solution of regularized linear programming problem in the environmental monitoring system. Kemerovo State Univ. Bull. 1(1), p35 (2014)

    Google Scholar 

  16. Renegar, J.: A framework for applying subgradient methods to conic optimization problems. (2015) arXiv:1503.02611

  17. Schuurmans, D., Southey, F., Holte, R.C.: The exponentiated subgradient algorithm for heuristic boolean programming. In: International Joint Conference on Artificial Intelligence, pp. 334–341 (2001)

  18. Onnheim, M., Gustavsson, E., Stromberg, A.B., Patriksson, M., Larsson, T.: Ergodic, primal convergence in dual subgradient schemes for convex programming, II: the case of inconsistent primal problems. Math. Program. 163(1–2), 57–84 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Wang, G., Zhang, H., Yu, S., Ding, S.: A family of the subgradient algorithm with several cosparsity inducing functions to the cosparse recovery problem. Pattern Recognit. Lett. 80, 64–69 (2016)

    Article  Google Scholar 

  20. Kirsch, A.: An Introduction to the Theory of Mathematical Inverse Problems, Volume 120 of Applied Mathematical Sciences., 2nd edn. Springer, New York (2011)

    Google Scholar 

  21. Wang, G.: Perturbation theory for weighted Moore-Penrose inverse. Commun. Appl. Math. Comput. 1(1), 48–60 (1981)

    MathSciNet  Google Scholar 

  22. Wei, Y., Wang, G.: PCR algorithm for parallel computing minimum-norm (T) least-squares (S) solution of inconsistent linear equations. Appl. Math. Comput. 133(2), 547–557 (2002)

    MathSciNet  MATH  Google Scholar 

  23. Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces. Springer, New York (2013)

    Book  MATH  Google Scholar 

  24. Bauschke, H.H., Wang, C., Wang, X., Xu, J.: On subgradient projectors. SIAM J. Optim. 25(2), 1064–1082 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Byrne, C.: Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 18(2), 441–453 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  26. Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20(1), 103–120 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  27. López, G., Martínmárquez, V., Wang, F., Xu, H.-K.: Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 28(8), 374–389 (2012)

    Article  MathSciNet  Google Scholar 

  28. Cegielski, A.: Landweber-type operator and its properties. In: Panorama of Mathematics: Pure and Applied, volume 658 of Contemporary Mathematics, pp. 139–148 (2016)

  29. Van Loan, C.F.: Generalizing the singular value decomposition. SIAM J. Numer. Anal. 13(1), 76–83 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  30. Han, G., Qu, G., Jiang, M.: Relaxation strategy for the Landweber method. Signal Process. 125, 87–96 (2016)

    Article  Google Scholar 

  31. Bauschke, H.H., Wang, C., Wang, X., Xu, J.: On the finite convergence of a projected cutter method. J. Optim. Theory Appl. 165(3), 901–916 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Caifang Wang is supported by National Natural Science Foundation of China (11401372).

Author information

Authors and Affiliations

  1. Department of Mathematics, Shanghai Maritime University, Shanghai, China

    Caifang Wang

Authors
  1. Caifang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Caifang Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, C. Properties of subgradient projection iteration when applying to linear imaging system. Optim Lett 13, 1285–1297 (2019). https://doi.org/10.1007/s11590-018-1321-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-018-1321-3

Keywords

Search

Navigation