Skip to main content
Springer Nature Link
Log in

A novel threshold changeable secret sharing scheme

  • Research Article
  • Published:
Frontiers of Computer Science Aims and scope Submit manuscript

Abstract

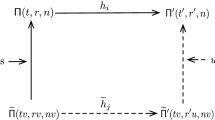
A (t, n) threshold secret sharing scheme is a fundamental tool in many security applications such as cloud computing and multiparty computing. In conventional threshold secret sharing schemes, like Shamir’s scheme based on a univariate polynomial, additional communication key share scheme is needed for shareholders to protect the secrecy of their shares if secret reconstruction is performed over a network. In the secret reconstruction, the threshold changeable secret sharing (TCSS) allows the threshold to be a dynamic value so that if some shares have been compromised in a given time, it needs more shares to reconstruct the secret. Recently, a new secret sharing scheme based on a bivariate polynomial is proposed in which shares generated initially by a dealer can be used not only to reconstruct the secret but also to protect the secrecy of shares when the secret reconstruction is performed over a network. In this paper, we further extend this scheme to enable it to be a TCSS without any modification. Our proposed TCSS is dealer-free and non-interactive. Shares generated by a dealer in our scheme can serve for three purposes, (a) to reconstruct a secret; (b) to protect the secrecy of shares if secret reconstruction is performed over a network; and (c) to enable the threshold changeable property.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Shamir A. How to share a secret. Communications of the ACM, 1979, 22(11): 612–613

    Article  MathSciNet  MATH  Google Scholar 

  2. Blakley G R. Safeguarding cryptographic keys. In: Proceedings of Managing Requirements Knowledge, International Workshop on IEEE Computer Society. 1979

  3. Harn L, Lin C. Strong (n, t, n) verifiable secret sharing scheme. Information Sciences, 2010, 180(16): 3059–3064

    Article  MathSciNet  MATH  Google Scholar 

  4. Harn L, Fuyou M, Chang C C. Verifiable secret sharing based on the Chinese remainder theorem. Security and Communication Networks, 2014, 7(6): 950–957

    Article  MATH  Google Scholar 

  5. Fuchsbauer G, Katz J, Naccache D. Efficient rational secret sharing in standard communication networks. In: Proceedings of Springer Theory of Cryptography Conference. 2010, 419–436

  6. Tartary C, Wang H X, Zhang Y. An efficient and information theoretically secure rational secret sharing scheme based on symmetric bivariate polynomials. International Journal of Foundations of Computer Science, 2011, 22(6): 1395–1416

    Article  MathSciNet  MATH  Google Scholar 

  7. Herzberg A, Jarecki S, Krawczyk H, Yung M. Proactive secret sharing or: how to cope with perpetual leakage. In: Proceedings of Springer Annual International Cryptology Conference. 1995, 339–352

  8. Harn L, Xu C F. Dynamic threshold secret reconstruction and its application to the threshold cryptography. Information Processing Letters, 2015, 115(11): 851–857

    Article  MathSciNet  MATH  Google Scholar 

  9. Harn L, Xu C F, Xia Z, Zhou J. How to share secret efficiently over networks. Journal of Security and Communication Networks, 2017, 2017(4): 1–6

    Google Scholar 

  10. Martin K, Pieprzyk J, Safavi-Naini R, Wang H. Changing thresholds in the absence of secure channels. In: Proceedings of Springer Australasian Conference on Information Security and Privacy. 1999, 177–191

  11. Steinfeld R, Wang H, Pieprzyk J. Lattice-based threshold changeability for standard Shamir secret-sharing schemes. IEEE Transactions on Information Theory, 2007, 53(7): 2542–2559

    Article  MathSciNet  MATH  Google Scholar 

  12. Asmuth C A, Bloom J. A modular approach to key safeguarding. IEEE Transactions on Information Theory, 1983, 29(2): 208–210

    Article  MathSciNet  MATH  Google Scholar 

  13. Blundo C, De Santis A, Herzberg A, Kutten S, Vaccaro U, Yung M. Perfectly-secure key distribution for dynamic conferences. Information and Computation, 1998, 146(1): 1–23

    Article  MathSciNet  MATH  Google Scholar 

  14. Blom R. An optimal class of symmetric key generation systems. In: Proceedings of Springer Workshop on the Theory and Application of of Cryptographic Techniques. 1984, 335–338

  15. Katz J, Koo C Y, Kumaresan R. Improving the round complexity of VSS in point-to point networks. Information and Computation, 2009, 207(8): 889–899

    Article  MathSciNet  MATH  Google Scholar 

  16. Kumaresan R, Patra A, Rangan C P. The round complexity of verifiable secret sharing: the statistical case. In: Proceedings of Springer International Conference on the Theory and Application of Cryptology and Information Security. 2010, 431–447

  17. Nikov V, Nikova S. On proactive secret sharing schemes. In: Proceedings of Springer International Workshop on Selected Areas in Cryptography. 2004, 308–325

  18. Zhang Z, Chee Y M, Ling S, Liu M, Wang H. Threshold changeable secret sharing schemes revisited. Theoretical Computer Science, 2012, 418: 106–115

    Article  MathSciNet  MATH  Google Scholar 

  19. Martin K M, Pieprzyk J, Safavi-Nain R, Wang H. Changing thresholds in the absence of secure channels. In: Proceedings of Springer Australasian Conference on Information Security and Privacy. 1999, 177–191

  20. Lou T, Tartary C. Analysis and design of multiple threshold changeable secret sharing. In: Proceedings of Springer International Conference on Cryptology and Network Security. 2008, 196–213

  21. Steinfeld R, Pieprzyk J, Wang H X. Lattice-based threshold changeability for standard CRT secret-sharing schemes. Finite Fields and Their Applications, 2006, 12(4): 653–680

    Article  MathSciNet  MATH  Google Scholar 

  22. Yuan L, Li M, Guo C, Choo K K R, Ren Y. Novel threshold changeable secret sharing schemes based on polynomial interpolation. PLoS ONE, 2016, 11(10): 1–19

    Article  Google Scholar 

  23. Meng K, Miao F, Huang W, Xiong Y. Threshold changeable secret sharing with secure secret reconstruction. Information Processing Letters, 2020, 157: 105928

    Article  MathSciNet  MATH  Google Scholar 

  24. Saniee K. A simple expression for multivariate lagrange interpolation. Journal of Society for Industrial and Applied Mathematics, 2007, 1–9

  25. Donald E K. The art of computer programming. Sorting and Searching, 1999, 3: 426–458

    Google Scholar 

  26. Rivest R L, Shamir A, Adleman L. A method for obtaining digital signatures and public key cryptosystems. Communications of the ACM, 1978, 21(2): 120–126

    Article  MathSciNet  MATH  Google Scholar 

  27. Denning D E R. Cryptography and Data Security. Massachusetts: Addison Wesley, 1982

    MATH  Google Scholar 

Download references

Acknowledgements

This work was partially supported by the National Natural Science Foundation of China (Grants Nos. 61772224, 62072133), the Fundamental Research Funds for the Central Universities (CCNU19TS019), the Research Planning Project of National Language Committee (YB135-40) and the key projects of Guangxi Natural Science Foundation (2018GXNSFDA281040). Lein Harn, Chingfang Hsu and Zhe Xia contributed equally to this work.

Author information

Authors and Affiliations

  1. Department of Computer Science Electrical Engineering, University of Missouri-Kansas City, Kansas City, MO, 64110, USA

    Lein Harn

  2. Computer School, Central China Normal University, Wuhan, 430079, China

    Chingfang Hsu

  3. Department of Computer Science, Wuhan University of Technology, Wuhan, 430071, China

    Zhe Xia

Authors
  1. Lein Harn
    View author publications

    Search author on:PubMed Google Scholar

  2. Chingfang Hsu
    View author publications

    Search author on:PubMed Google Scholar

  3. Zhe Xia
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Chingfang Hsu.

Additional information

Lein Harn received the BS degree in electrical engineering from the Taiwan University, China in 1977, the MS degree in electrical engineering from the State University of New York-Stony Brook, USA in 1980, and the Ph D degree in electrical engineering from the University of Minnesota, USA in 1984. He is currently a Professor at the Department of Electrical and Computer Engineering, University of Missouri, USA. He is currently investigating new ways of using secret sharing in various applications.

Chingfang Hsu received the MEng and the PhD degrees in information security from the Huazhong University of Science and Technology, China in 2006 and 2010, respectively. From Sep. 2010 to Mar. 2013, she was a Research Fellow at the Huazhong University of Science and Technology, China. She is currently an Assistant Professor at Central China Normal University, China. Her research interests are in cryptography and network security, especially in secret sharing and its applications.

Zhe Xia received the MEng and the PhD degrees in information security from University of Surrey, UK in 2005 and 2009, respectively. From 2009 to 2013, he was a Research Fellow at University of Surrey, UK. He is currently an Assistant Professor at Department of Computer Science, Wuhan University of Technology, China. His research interests are in cryptography and network security, especially in secret sharing and its applications.

Electronic supplementary material

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Harn, L., Hsu, C. & Xia, Z. A novel threshold changeable secret sharing scheme. Front. Comput. Sci. 16, 161807 (2022). https://doi.org/10.1007/s11704-020-0300-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11704-020-0300-x

Keywords