1 Introduction

In security applications of wireless sensor network (WSN) as in military sensing, surveillance and battle field tracking, confidentiality, integrity and authentication are of big interest to communicate with a minimum level of trust. But low resources will impose limitations on the cryptographic algorithms implemented in the nodes. It is needed to design an efficient algorithm to fulfil its purpose, and in the same time, it should be relatively simple so it can be implemented and used with a minimum cost. Hence, a trade-off between security and efficiency should be fulfilled to reach a realistic and applicable cipher to be used in real-world secure communications like WSN. Till now, partial encryption [7] and ultralightweight block ciphers, as for example [1–6], emerged as the suitable solution to be employed in resources-constrained devices like WSN nodes. Here, our aim is to study the security of a partial video encryption method, proposed by Yang and Sun [7], that can be used in video nodes in a WSN. The scheme under study includes two key operations: takes the DCT coefficients of an MPEG I-frame as an input to be shuffled and mixed I-frames with a chaotic pseudo-random number sequence, and uses three chaotic maps (two coupling chaotic maps and one chaotic map). This method can be used in video nodes in a WSN because it will only encrypt significant parts of the sequence, and so, computational energy of the node will be saved. However, by analyzing this encryption method, we have found that the trade-off between security and efficiency is not fulfilled. We demonstrate that this cryptosystem has serious weaknesses in the shuffling and the mixing processes which makes it vulnerable to chosen plaintext attack. Indeed, two chosen plaintext–ciphertext pairs were enough to recover the equivalent keys which are the keystreams used in the scrambling process and in the mixing process. This problem can be generalized to most of the many proposed ciphers where in each application, one will propose its own cipher to be implemented in that specific application without being tested or widely approved. It is important to note that designing a secured cipher is a hard task and needs a robust mathematical background followed by an exhaustive cryptanalysis work. Here rises the practical question: does the application developers need to design their own ciphers for their specific applications or do better take the most tested, widely approved cryptographic designs and just use them in a proper way to fit their applications?

The outline of this work is as follows. In Sect. 2, a brief description of the cryptosystem under study is presented. Section 3 demonstrates how to implement the chosen plaintext attack. Section 4 explains the recovering scenario using the results of the chosen plaintext attack. Section 5 computes the computational complexity of the break and the whole recovering scenario. Finally, Sect. 6 concludes this letter.

2 The cryptosystem under study

2.1 Brief description

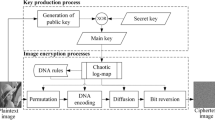
A compressed video sequence shows three types of frames which are freely arranged by the encoder in the form: \( I \, P \, B \, B \, P \, B \, B \ldots \). It should be noted that the I-frame which is the beginning of each video sequence is the most important frame. Indeed, P-frame can be predicted from the I-frame and the previous P-frame, and B-frames are greatly compressed and cannot provide reference to the later frames. Hence, we can obviously conclude that the encryption of the I-frame will act directly on the entire MPEG video sequence. To encrypt the I-frame, the cryptosystem proposed in [7] consists of two main parts: a scrambling process of the I-frame and then a confusion process of the resultant scrambled I-frame. We note that we give a clearer presentation of the algorithm and use much more proper notations than the source paper [7] to describe their cryptosystem. The encryption scenario leading to encrypt the I-frame \(I\) to the ciphered I-frame \(C\) is described as follows:

  1. 1.

    DCT transformation: Generate the DCT coefficients of the I-frame \(I\) and note the result as \(D_I\).

  2. 2.

    Scrambling process: First, the DCT coefficients \(D_I\) of the I-frame \(I\) of size \(M\times N\) are scrambled with two keystreams \(\omega _i,\,i=1,2, \ldots , M\) and \(\pi _j,\,j=1,2, \ldots , N\) obtained from arrangement of two chaotic sequences separately by magnitude \(x_{i}\) and \(y_{j}\). The sequences \(x_{i}\) and \(y_{j}\) are generated from a double coupling logistic map given by Eq. (1) having as initial condition (\(x_{0},\,y_{0}\)).

    $$\begin{aligned} \left\{ {\begin{array} {lc} x_{n+1}&{}= \mu _{x} x_{n}(1-x_{n})\\ y_{n+1}&{}= \mu _{y} y_{n}(1-y_{n}),\\ \end{array}} \right. \end{aligned}$$
    (1)

    where \(\mu _{x}\) and \(\mu _{y}\) are design parameters, and \(x_{n}\) and \(y_{n}\) are the values of the chaotic sequences. The parameters are altered according to the following equations:

    $$\begin{aligned} \mu _{x}= \left\{ {\begin{array} {ll} 3.9, \, \, \, \,\, &{}\hbox {if} \, \, \, \, 0<y_{j}<0.5\\ 3.9888, \, \, \, \, &{}\hbox {if} \, \, \, 0.5<y_{j}\end{array}} \right. \end{aligned}$$
    (2)
    $$\begin{aligned} \mu _{y}= \left\{ {\begin{array} {ll} 3.9444, \, \, \, \,\,&{} \hbox {if} \, \, \, \, 0<x_{i}<0.5\\ 4.0, \, \, \, \,&{}\hbox {if} \, \, \, 0.5<x_{i}\\ \end{array}} \right. \end{aligned}$$
    (3)

    As a result, we obtain an I-frame \(S\) with scrambled DCT coefficients noted \(D_S\).

  3. 3.

    Mixing Process: The scrambled DCT coefficients in \(D_S\) are arranged as a vector to obtain the coefficients \(D_{S}(k),\,k=1,2 \ldots , M\times N\), and transformed on \(D_{C}(k)\) by applying the following equation:

    $$\begin{aligned} D_{C}(k)=D_{S}(k) \times (1+z_k), \end{aligned}$$
    (4)

    where \(z_k\) is a keystream generated by Eq. (5) departing from an initial condition \(z_0\).

    $$\begin{aligned}&z_{k+1}= 1-\lambda z_k^{2}\nonumber \\&z_k \in [-1,1] \quad \;(k=1,2 \ldots , M\times N) \end{aligned}$$
    (5)

    We obtain the matrix \(D_C\) formed by arranging the DCT coefficients \(D_{C}(k),\,k=1,2 \ldots , M\times N\) in a matrix of size \(M\times N\).

  4. 4.

    IDCT Transformation: The ciphered I-frame \(C\) is then obtained by doing the inverse DCT transformation on \(D_C\):

    $$\begin{aligned} C=IDCT(D_C) \end{aligned}$$

As claimed in [7], the cryptosystem key is composed by four subkeys \(K = (K_{1}=x_{0},\,K_{2}=y_{0},K_{3}=z_0,\,K_{4}=\lambda )\).

2.2 Equivalent keys as the main problem of the scheme

The cryptosystem under study consists on two modules:

  1. 1.

    A shuffling process of the DCT coefficient’s positions of the I-frame using the keystreams \(\omega _i,\,i=1,2, \ldots , M\) and \(\pi _j,\,j=1,2, \ldots , N\) for an I-frame of size \(M\times N\). Then,

  2. 2.

    A confusion process where the values of the shuffled DCT coefficients are changed using the sequence \(z_k,\,k=1,2, \ldots , M\times N\) applied in the Eq. (4).

So, decrypting the ciphered I-frame can be accomplished by computing the keytreams \(\omega _i,\,\pi _j\) and \(z_k\) (see Fig. 1). This weakness will be used to design a chosen plaintext attack to recover the cryptosystem key.

Fig. 1
figure 1

Equivalent description of the cryptosystem using equivalent keys

Full size image

The obvious weakness of the cryptosystem here is the fact that the keystream generation is the same for every plaintext–ciphertext pair. Next, it is shown how to recover the keystream using a chosen plaintext attack. It is to note that the break of the encryption method is completely independent of the method that is used to generate the keystreams for the permutation process and for the mixing process. That is why no matter what chaotic map was used in the generation of the keystreams, the break still work. That is why we will consider as secret equivalent keys the keystreams (\(\omega _i,\,\pi _j\) and \(z_k\)) instead of the original keys. These equivalent keys can be generated randomly independently from any chaotic map. It is also important to note that this break is independent from the application from being selective encryption or complete encryption.

3 Chosen plaintext attack

The chosen plaintext attack assumes that the adversary obtained temporary access to the encryption machinery. Hence, he can choose any input (plaintext) to generate the corresponding output (ciphertext) and try to recover the key or an equivalent key or the original plaintext of an intercepted ciphertext. In the following, we describe how to retrieve the equivalent keys (\(\omega _i,\pi _j\) and \(z_k\)) by choosing two special plaintext–ciphertext pairs (\(I_1,\,C_1\)) and (\(I_2,\,C_2\)).

  1. 1.

    We request the ciphertext of the I-frame \(I_1\) having as DCT coefficients values all in 1 meaning:

    $$\begin{aligned} D_{I1}(k)= 1 \end{aligned}$$

    for every \(k=1,2,\ldots M \times N\) meaning as follows:

    $$\begin{aligned} \footnotesize D_{I1}=\begin{pmatrix} 1 &{}\quad 1 &{}\quad \ldots &{}\quad 1 \\ 1 &{}\quad 1&{}\quad \ldots &{}\quad 1 \\ \vdots &{}\quad \vdots &{}\quad \ldots &{}\quad \vdots \\ 1 &{}\quad 1 &{}\quad \ldots &{}\quad 1 \end{pmatrix} \end{aligned}$$

    We obtain the ciphertext \(C_1\) having as DCT coefficients \(D_{C1}(k)\). Since the permutation process has no effect on the DCT transformations of I-frames with equal entries, the result of the permutation stage is the same as the entry. Therefore, we can get the keystream \(z_k\) from \(D_{C1}(k)\) as follows:

    $$\begin{aligned} z_k=D_{C1}(k)-1, \quad k=1,2,\ldots , M\times N \end{aligned}$$
    (6)

    The Algorithm 1 named get\(z\), was applied to retrieve \(z_k\), and it is described as follows:

    figure a
  2. 2.

    We request now the ciphertext of an I-frame \(M\times N\) noted \(I_2\) having as DCT coefficients:

    $$\begin{aligned} D_{I2}(k)= k \end{aligned}$$

    for every \(k=1,2,\ldots , M \times N\) which can be written as:

    $$\begin{aligned} \footnotesize D_{I2}=\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 1 &{} 2 &{} \ldots &{} N \\ N+1 &{}N+2 &{} \ldots &{} 2N \\ \vdots &{} \vdots &{} \ldots &{} \vdots \\ (M-1)N+1 &{} (M-1)N+2 &{} \ldots &{} MN \end{array}\right) \end{aligned}$$

    To show an example, we will consider that \(M{=} N{=} 4\), so

    $$\begin{aligned} D_{I2}=\begin{pmatrix} 1 &{}\quad 2 &{}\quad 3 &{}\quad 4 \\ 5 &{}\quad 6 &{}\quad 7 &{}\quad 8 \\ 9 &{}\quad 10&{}\quad 11 &{}\quad 12 \\ 13 &{}\quad 14 &{}\quad 15 &{}\quad 16 \end{pmatrix} \end{aligned}$$

    The corresponding ciphered I-frame is noted \(C_2\) having as DCT transformation \(D_{C2}\). With the calculated keystream \(z_k\) in Eq. 6 in step (1), we generate the shuffled I-frame with DCT coefficients \(D_{S2}=D_{S2}(1)D_{S2}(2) \ldots \) applying the following equation:

    $$\begin{aligned} D_{S2}(k)= \frac{D_{C2}(k)}{1 + z_k} \end{aligned}$$
    (7)

    With the given example, we find that:

    $$\begin{aligned} D_{S2}=\begin{pmatrix} 12 &{}\quad 10 &{}\quad 9 &{}\quad 11 \\ 16 &{}\quad 14 &{}\quad 13 &{}\quad 15 \\ 8&{}\quad 6 &{}\quad 5 &{}\quad 7 \\ 4 &{}\quad 2 &{}\quad 1 &{}\quad 3 \end{pmatrix} \end{aligned}$$

    So, we can determinate the keystream \(\omega _i\) where \(i=1,2, \ldots , M\) and \(\pi _j\) where \(j=1,2, \ldots , N\) by comparing the shuffled matrix of coefficients \(D_{S2}\) and the matrix \(D_{I2}\). The Algorithm 2 named get \(\omega _i\)-\(\pi _j\), which was applied to retrieve \(\omega _i\) and \(\pi _j\), is described as follows:

figure b

From Algorithm 2, the equivalent keys which are the keystreams \(z_k\) and the two permutation vectors \(\omega _i\) and \(\pi _j\) were successfully retrieved and can be used later to recover any intercepted ciphered I-frame \(C\).

3.1 Feasibility of the chosen plaintext attack

The keystreams were successfully recovered by choosing two pairs of (plain I-frame/ciphered I-frame). To be specific, we will take the example of \((4\times 4)\) matrixes.

The first chosen I-frame was

\(I_1=\footnotesize {\begin{pmatrix} 3.7013 &{}\quad -0.7362 &{}\quad 0.7362 &{}\quad 0.1464 \\ -0.7362 &{}\quad 0.1464 &{}\quad -0.1464 &{}\quad -0.0291 \\ 0.7362 &{}\quad -0.1464 &{}\quad 0.1464 &{}\quad 0.0291 \\ 0.1464 &{}\quad -0.0291 &{}\quad 0.0291 &{}\quad 0.0058 \end{pmatrix}}\) having as DCT transformation an all ones matrix: \(DCT(I_1)=\begin{pmatrix} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \end{pmatrix}\)

The second chosen I-frame was:

\(I_2=\footnotesize {\begin{pmatrix} 27.4139 &{}\quad -9.6834 &{}\quad 5.8356 &{}\quad 0.0023 \\ -22.3747 &{}\quad 5.2921 &{}\quad -4.5267 &{}\quad -0.6700 \\ 6.9837 &{}\quad -2.2306 &{}\quad 1.4653 &{}\quad 0.0610 \\ -3.2449 &{}\quad 0.4781 &{}\quad -0.6303 &{}\quad -0.1712 \end{pmatrix}}\) having as DCT transformation the matrix: \(DCT(I_2)=\begin{pmatrix} 1 &{}\quad 2 &{}\quad 3 &{}\quad 4 \\ 5 &{}\quad 6 &{}\quad 7 &{}\quad 8 \\ 9 &{}\quad 10 &{}\quad 11 &{}\quad 12 \\ 13 &{}\quad 14 &{}\quad 15 &{}\quad 16 \end{pmatrix}\)

Two possible scenarios can be followed to maintain the chosen plaintext attack:

  1. 1.

    If the input of the encryption machinery is available we can inject directly the transformed I-frame to DCT domain to the encryption machinery. This means we can inject directly \(DCT(I_1)\) to break the mixing keystream and then \(DCT(I_2)\) to recover the permutation keystreams.

  2. 2.

    If the entry of the encryption machinery is not directly available but can be accessed only through the DCT transformation stage, then in this case, we are forced to inject the inverse DCT transformations of \(DCT(I_1)\) and \(DCT(I_2)\) to recover the mixing and the permutation keystreams. This mean we are forced to inject \(I_1\) then \(I_2\) to the block formed by the DCT transformation followed by the encryption machinery.

It is important to note that the two chosen I-frames in the chosen plaintext attack are not natural images but they are special images that has no physical sense meaning they cannot be correctly visualized through an image decoder because they are formed by real values pixels.

4 Recovering scenario using the chosen plaintext attack results

Assume that we have a ciphered I-frame \(C\) to decrypt without knowing the key \(K\). We will describe the steps leading to recover the plain I-frame \(I\) from the ciphered I-frame \(C\) by exploiting the results gained from the chosen plaintext attack.

The chosen plaintext attack was used to determine the equivalent keys which are the keystream \(z_k\) and the two permutation vectors \(\omega _i\) and \(\pi _j\). These equivalent keys are equivalent to the original key \(K=(K_{1}=x_{0},\,K_{2}=y_{0},\,K_{3}=z_0,\,K_{4}=\lambda \)). Given any ciphered I-frame \(C\), we explain how to recover its plain I-frame \(I\) using the derived equivalent keys. From \(C\), we can get its DCT transformation named \(D_C\), then the permuted DCT coefficients matrix \(D_S\) can be calculated using \(D_C\) and the retrieved keystream \(z_k\) by applying the following equation:

$$\begin{aligned} D_{S}(k)=\frac{D_C(k)}{1+z_k}, \,\,\,\, k=1,2, \ldots , M\times N \end{aligned}$$
(8)
figure c

These DCT coefficients are then rearranged in a matrix of size \(M \times N\). Then, the original DCT coefficients matrix \(D_I\) is obtained using the retrieved permuatation vectors \(\omega _i\) and \(\pi _j\) by applying the following:

$$\begin{aligned} D_I(i,j) \leftarrow D_{S}(\omega _i,\pi _j) \end{aligned}$$
(9)

As a conclusion, the following algorithm (Algorithm 3) summarizes how to decrypt any ciphered I-frame \(C\) by retrieving the equivalent keys using two plaintext–ciphertext pairs:

The Fig. 2 shows the experimental results of the successful recovering process for an I-frame of size \(256\times 256\).

Fig. 2
figure 2

Experimental results of the proposed attack: a original plain I-frame \(P\), b encrypted I-frame, c recovered I-frame using the chosen plaintext attack

Full size image

5 Computation complexity

The breaking method is based on two main steps. The first one consists on determining the keystream \(z_k\) using a chosen plaintext–ciphertext pair \((D_{I1},D_{C1})\) which are the DCT transformations of the actual I-frames pair. In the second step, equivalent keys \((\omega _i,\pi _j)\) are retrieved using another chosen plaintext–ciphertext pair \((D_{I2},D_{C2})\). In each step, the adversary access one time to the encryption machinery. Now, we count two accesses to the encryption machinery that we should consider in the total cost of the break.

For the first step, given an I-frame of size \(M\times N\), it is needed (\(M\times N\)) CPU operations (substraction operations), related to Eq. (6) to generate the keystream \(z_k\).

For the second step of the breaking process, \((2 \times M\times N)\) CPU operations (addition \(+\) division) are needed to perform Eq. (7). Then, \((M\times N)^2\) comparison operations are needed to retrieve the permutation vectors given by Algorithm 2. Giving the retrieved equivalent key, the recovering scenario costs \((3\times M\times N)\) CPU operations if we suppose that we deal directly with DCT transformations of I-frames because \((2 \times M\times N)\) operations are needed to perform Eq. (8), and \((M\times N)\) operations are needed to perform the assignment of Eq. (9).

As a result, the computational complexity of the breaking process for an I-frame of size \(M\times N\), is:

$$\begin{aligned}&\!\!\!((M\times N)^2 + (6 \times M\times N)\\&\quad + (2 \times { encryption-process-cost})) \, \hbox {CPU operations}. \end{aligned}$$

We conclude that retrieving the permutation vectors using Algorithm 2 is the most consuming part of this break and the cost will increase in quadratic manner versus the size of the handled I-frame. Finally, we conclude that the complexity of the described attack is \(\Theta ((M\times N)^2)\).

To evaluate this cost on a machine, we proceed to measure the breaking time needed for different size of the I-frame. The results are shown in Table 1. We note that the breaking algorithm is implemented in Matlab 7.5 on a personal computer with an Intel Centrino 1.6 GHz processor and 512 MB of RAM Memory.

Table 1 Breaking time for different I-frame sizes
Full size table

6 Conclusion

This paper demonstrates, through a cipher example, that designing proprietary cryptosystems for specific applications will certainly be weak against various practically feasible attacks like known/chosen plaintext attacks. Instead practitioners should follow what is going on in the cryptographic community and examine the performance of the state-of-the-art ciphers and fit those well-known ciphers for their applications. They will know at least the complexity of attacking their applications and then try to make a trade-off between security and efficiency. The example studied in this paper is a video encryption method based on chaotic maps in DCT domain. We have found that only two plaintext–ciphertext pairs were enough to totaly break the cryptosystem. Further, the proposed attack is economical in term of the computation complexity.