Investigating different reverse channels in a closed-loop supply chain: a power perspective

Abstract

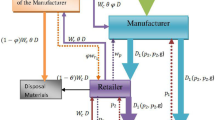
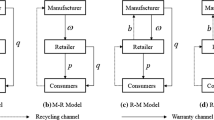
This study investigates reverse channel choice for a bi-level closed-loop supply chain consisting of a manufacturer and a retailer. In the forward channel, the manufacturer sells the products through the retailer. We consider three collection channels to collect end-of-use products for the reverse channel: (1) retailer collection (R model), (2) manufacturer and retailer hybrid collection (MRH model), and (3) manufacturer and retailer competitive collection (MRC model). This study considers both manufacturer leadership and retailer leadership for all these three models. After obtaining the members' optimal decisions in the different models using backward induction, the models were applied to a vacuum cleaner company's data in Iran. A comparison of these models shows that the retailer leadership was better than the manufacturer leadership. From the manufacturer leadership perspective, the MRH model is the best one. From the retailer leadership perspective, the prices, the retailer collection rate, and the retail profit are the same in the R and MRH models, while the total collection rate and the total yield are more extensive in the MRH model than in the R model. The MRH model is better than the MRC model at any competition intensity. Moreover, this study indicates that the range of competition intensity between two collection channels in which the MRC model outperforms the R model is different under the retailer leadership and the manufacturer leadership. The results of this study can be used as a reference for reverse channel selection. Finally, we perform a sensitivity analysis for the model parameters.

Appendices

Appendices

Appendix A

R-M Model, retailer collection-manufacturer Stackelberg

• Problem of retailer

To investigate the concavity of retailer profit function, its Hessian matrix has to be formed as,

$$ \frac{{\partial \Pi_{R}^{R - M} }}{{\partial p^{R - M} }} = (\phi - \beta p) - \beta \left( {p - W + (b - A)\tau_{R}^{R - M} } \right) $$

(A-1)

$$ \frac{{\partial \Pi_{R}^{R - M} }}{{\partial \tau_{R}^{R - M} }} = (\phi - \beta p)(b - A) - 2C_{L} \tau_{R}^{R - M} $$

(A-2)

$$ H(\Pi_{R}^{R - M} ) = \left[ {\begin{array}{*{20}c} { - 2\beta } & { - \beta (b - A)} \\ { - \beta (b - A)} & { - 2C_{L} } \\ \end{array} } \right] $$

(A-3)

For the retailer profit function to be concave, the determinants of the above Hessian matrix are required to be negative and positive decussate—i.e. $\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0$- in which case, if $4C_{L} > \beta (b - A)^{2}$, the retailer profit function is concave compared to $p^{R - M} , \, \tau_{R}^{R - M}$ and it has a unique optimal solution as,

$$ \hat{p}^{R - M} = \frac{{2C_{L} (\phi + \beta W) - \beta \phi (b - A)^{2} }}{{\beta \left[ {4C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-4)

$$ \hat{\tau }_{R}^{R - M} = \frac{(\phi - \beta W)(b - A)}{{4C_{L} - \beta (b - A)^{2} }} $$

(A-5)

• Problem of manufacturer

replacing (A-4) and (A-5) in the manufacturer profit function and considering $Y = 4C_{L} - \beta (b - A)^{2}$ and $S = (b - A)(\Delta - b)$, we will have,

$$ \hat{\Pi }_{M}^{R - M} = \frac{{2C_{L} (\phi - \beta W)}}{Y}\left[ {W - C_{m} + \frac{S(\phi - \beta W)}{Y}} \right] $$

(A-6)

To investigate the concavity of the manufacturer profit function, the second derivative of the above equation should be calculated due to the wholesale price $W^{R - M}$ as,

$$ \frac{{\partial \hat{\Pi }_{M}^{R - M} }}{{\partial W^{R - M} }} = \frac{{2C_{L} }}{Y}\left[ {\phi - 2\beta W + \beta C_{m} - \frac{2\beta S(\phi - \beta W)}{Y}} \right] $$

(A-7)

$$ \frac{{\partial^{2} \hat{\Pi }_{M}^{R - M} }}{{\partial (W^{R - M} )^{2} }} = \frac{{ - 4C_{L} \beta }}{Y} + \frac{{4\beta^{2} C_{L} S}}{{Y^{2} }} $$

(A-8)

Considering $\frac{{\partial^{2} \hat{\Pi }_{M}^{R - M} }}{{\partial (W^{R - M} )^{2} }} < 0$, the manufacturer profit function is concave. Now, the wholesale price is obtained as,

$$ \hat{W}^{R - M} = \frac{{(\phi + \beta C_{m} )Y - 2\beta S\phi }}{{2\beta Y - 2\beta^{2} S}} $$

(A-9)

Replacing (9) in the manufacturer profit function gives

$$ \hat{\Pi }_{M}^{R - M} = \frac{{C_{L} (\phi - \beta C_{m} )^{2} }}{{2\beta \left[ {Y - \beta S} \right]}} $$

(A-10)

Since the above equation is always incremental to b, b equals to its upper limit and we have,

$$ b = \Delta $$

(A-11)

Now the wholesale price is obtained as

$$ W^{R - M*} = \frac{{\phi + \beta C_{m} }}{2\beta } $$

(A-12)

Replacing $W^{R - M*}$ in $\hat{p}^{R - M} , \, \hat{\tau }_{R}^{R - M}$ equations gives the optimal wholesale prices and retailer collection rate as,

$$ p^{R - M*} = \frac{{C_{L} (3\phi + \beta C_{m} ) - \beta \phi (\Delta - A)^{2} }}{{\beta [4C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-13)

$$ \tau_{R}^{R - M*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{2[4C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-14)

Limitation $0 \le \tau_{R}^{R - M*} < 1$ completes this section.

R-R Model, retailer collection-retailer Stackelberg

• Problem of manufacturer

Since the manufacturer’s profit increases as W increases and given limitation $w < p$, let us assume the manufacturer’s profit to be the average of the retailer’s profit margin and wholesale price as,

$$ \hat{W}^{R - R} = \frac{{p^{R - R} + C_{m} }}{2} $$

(A-15)

The above inference is similar to the approach assumption employed in Taleizadeh et al. (2017), Maiti and Giri (2015), Giri et al. (2017), and SeyedEsfahani et al. (2011) to solve the retailer Stackelberg model.

• Problem of retailer

replacing $\hat{W}^{R - R}$ in the retailer profit function gives,

$$ \hat{\Pi }_{R}^{R - R} = \frac{{(p - C_{m} )}}{2}(\phi - \beta p) + (\phi - \beta p)(b - A)\tau_{R}^{R - R} - C_{L} (\tau_{R}^{R - R} )^{2} $$

(A-16)

Let us investigate the concavity of the retailer profit function as,

$$ \frac{{\partial \hat{\Pi }_{R}^{R - R} }}{{\partial p^{R - R} }} = \frac{(\phi - \beta p)}{2} - \frac{{\beta (p - C_{m} )}}{2} - \beta (b - A)\tau_{R}^{R - R} $$

(A-17)

$$ \frac{{\partial \hat{\Pi }_{R}^{R - R} }}{{\partial \tau_{R}^{R - R} }} = (\phi - \beta p)(b - A) - 2C_{L} \tau_{R}^{R - R} $$

(A18)

$$ H(\hat{\Pi }_{R}^{R - R} ) = \left[ {\begin{array}{*{20}c} { - \beta } & { - \beta (b - A)} \\ { - \beta (b - A)} & { - 2C_{L} } \\ \end{array} } \right] $$

(A-19)

For the retailer profit function to be concave, its Hessian matrix is required to be negative definite. Thus, the retailer profit function will be concave with a unique optimal solution if the following condition is satisfied,

$$ 2C_{L} > \beta (b - A)^{2} $$

(A-20)

Now, the retailer’s best reactions will be as follows using the first-order condition,

$$ \hat{p}^{R - R} = \frac{{C_{L} (\phi + \beta C_{m} ) - \beta \phi (b - A)^{2} }}{{\beta \left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-21)

$$ \hat{\tau }_{R}^{R - R} = \frac{{(\phi - \beta C_{m} )(b - A)}}{{2\left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-22)

Replacing $\hat{p}^{R - R}$ in $\hat{W}^{R - R}$ equation gives the wholesale price as,

$$ \hat{W}^{R - R} = \frac{{C_{L} (\phi + 3\beta C_{m} ) - \beta (b - A)^{2} (\phi + \beta C_{m} )}}{{2\beta \left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-23)

Now, the following equation is obtained by replacing (A-24) in the manufacturer profit function as,

$$ \hat{\Pi }_{M}^{R - R} = \frac{{C_{L} (\phi - \beta C_{m} )^{2} }}{{2\beta Y^{2} }}\left[ {C_{L} - \beta (b - A)^{2} + \beta S} \right] $$

(A-24)

According to Savaskan et al. (2004) and Hong et al. (2013), the manufacturer transfers the entire saving resulted from remanufacturing to the retailer because of the retailer’s collection rate increases as b increases, resulting in the reduced manufacturing cost $\overline{C} = C_{m} - \Delta \tau$. Also, an increase in the transfer price makes the retailer reduce the retail price. Thus, the increased demand and reduced manufacturing cost increases the profit, and thus $b = \Delta$.

The lower the transfer price (b) is than the net saved costs resulted from remanufacturing ($\Delta$) compared to when $b = \Delta$, the prices decline and the collection rate rises lower due to the double marginalization and thus the profit rises lower. Of course, it can be observed in equations $\hat{\rm p}^{{\rm R - R}} ,\,\hat{\uptau }_{\rm R}^{{{\rm R} - {\rm R}}} ,{\text{ }}\hat{\rm W}^{{{\rm R} - {\rm R}}}$ that an increase in transfer price b, retail price decreases, and the collection rate increases. Demand ($\phi - \beta p$) can be increased via a reduction in the retail price and an increase in the collection rate reduces the manufacturing cost. Thus, $\frac{{\partial \hat{\Pi }_{M}^{R - R} }}{\partial b} > 0$ and $b = \Delta$.

Now, the optimal wholesale price, retail price, and retailer’s collection rate are obtained as,

$$ W^{R - R*} = \frac{{C_{L} (\phi + 3\beta C_{m} ) - \beta (\Delta - A)^{2} (\phi + \beta C_{m} )}}{{2\beta [2C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-25)

$$ p^{R - R*} = \frac{{C_{L} (\phi + \beta C_{m} ) - \beta \phi (\Delta - A)^{2} }}{{\beta [2C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-26)

$$ \tau_{R}^{R - R*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{2[2C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-27)

Limitation $0 \le \tau_{R}^{R - R*} < 1$ completes this section.

Appendix B

MR-M Model, manufacturer, and retailer hybrid collection: manufacturer Stackelberg

• Problem of retailer

First, let’s investigate the concavity of the retailer profit function.

$$ \frac{{\partial \Pi_{R}^{MR - M} }}{{\partial p^{MR - M} }} = (\phi + \beta W) - 2\beta p - \beta (b - A)\tau_{R}^{MR - M} $$

(A-28)

$$ \frac{{\partial \Pi_{R}^{MR - M} }}{{\partial \tau_{R}^{MR - M} }} = (\phi - \beta p)(b - A) - 2C_{L} \tau_{R}^{MR - M} $$

(A-29)

$$ H(\Pi_{R}^{MR - M} ) = \left[ {\begin{array}{*{20}c} { - 2\beta } & { - \beta (b - A)} \\ { - \beta (b - A)} & { - 2C_{L} } \\ \end{array} } \right] $$

(A-30)

For the retailer profit function to be concave, the determinants of the above Hessian matrix have to be positive and negative decussate—i.e. $\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0$. In this case, the retailer profit function will be concave compared to $p^{MR - M} , \, \tau_{R}^{MR - M}$ with a unique optimal solution if $4C_{L} > \beta (b - A)^{2}$. Now, the retailer’s optimal decisions are obtained by solving the following equations using the first-order condition.

$$ \frac{{\partial \Pi_{R}^{MR - M} }}{{\partial p^{MR - M} }} = 0 $$

(A-31)

$$ \frac{{\partial \Pi_{R}^{MR - M} }}{{\partial \tau_{R}^{MR - M} }} = 0 $$

(A-32)

The retailer’s optimal decisions will be as follows:

$$ \hat{p}^{MR - M} = \frac{{2C_{L} (\phi + \beta W) - \beta \phi (b - A)^{2} }}{{\beta \left[ {4C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-33)

$$ \hat{\tau }_{R}^{MR - M} = \frac{(\phi - \beta W)(b - A)}{{4C_{L} - \beta (b - A)^{2} }} $$

(A-34)

• Problem of manufacturer

considering the retailer solutions and, $Y = 4C_{L} - \beta (b - A)^{2}$ and $S = (b - A)(\Delta - b)$, the manufacturer profit function will be as follows:

$$ \hat{\Pi }_{M}^{MR - M} = \frac{{2C_{L} (\phi - \beta W)}}{Y}\left[ {W - C_{m} + (\Delta - A)\tau_{M}^{MR - M} + \frac{S(\phi - \beta W)}{Y}} \right] - C_{L} (\tau_{M}^{MR - M} )^{2} $$

(A-35)

Now let us investigate the concavity of the manufacturer profit function,

$$ \frac{{\partial \hat{\Pi }_{M}^{MR - M} }}{{\partial W^{MR - M} }} = \frac{{2C_{L} }}{Y}\left[ {\phi + \beta C_{m} - 2\beta W - \beta (\Delta - A)\tau_{M}^{MR - M} - \frac{2\beta S(\phi - \beta W)}{Y}} \right] $$

(A-36)

$$ \frac{{\partial \hat{\Pi }_{M}^{MR - M} }}{{\partial \tau_{M}^{MR - M} }} = \frac{{2C_{L} (\phi - \beta W)(\Delta - A)}}{Y} - 2C_{L} \tau_{M}^{MR - M} $$

(A-37)

$$ H(\hat{\Pi }_{M}^{MR - M} ) = \left[ {\begin{array}{*{20}c} {\frac{{2C_{L} }}{Y}\left[ { - 2\beta + \frac{{2\beta^{2} S}}{Y}} \right]} & { - \frac{{2C_{L} \beta (\Delta - A)}}{Y}} \\ { - \frac{{2C_{L} \beta (\Delta - A)}}{Y}} & { - 2C_{L} } \\ \end{array} } \right] $$

(A-38)

For the manufacturer profit function to be concave compared to $W^{MR - M} , \, \tau_{M}^{MR - M}$, the determinants of the minor of the hessian matrix are required to be negative and positive decussate. In this case, the Hessian matrix and manufacturer profit function will be negative and concave, respectively, if

$$ 8C_{L} > \beta \left[ {2(b - A)^{2} + 2(b - A)(\Delta - b) + (\Delta - A)^{2} } \right] $$

(A-39)

The same as with the previous model, $\frac{{\partial \Pi_{M}^{MR - R} }}{\partial b} > 0$ and $b = \Delta$ in this model.

If $8C_{L} > \beta \left[ {2(b - A)^{2} + 2(b - A)(\Delta - b) + (\Delta - A)^{2} } \right]$, the optimal wholesale price and manufacturer’s collection rate will be as follows,

$$ W^{MR - M*} = \frac{{4C_{L} (\phi + \beta C_{m} ) - \beta (\Delta - A)^{2} (2\phi + \beta C_{m} )}}{{\beta [8C_{L} - 3\beta (\Delta - A)^{2} ]}} $$

(A-40)

$$ \tau_{M}^{MR - M*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{8C_{L} - 3\beta (\Delta - A)^{2} }} $$

(A-41)

Replacing $W^{MR - M*}$ in $\hat{p}^{MR - M}$ and $\hat{\tau }_{M}^{MR - M}$ equations give the optimal wholesale price and retailer’s collection rate as,

$$ p^{MR - M*} = \frac{{2C_{L} (3\phi + \beta C_{m} ) - 3\beta \phi (\Delta - A)^{2} }}{{\beta [8C_{L} - 3\beta (\Delta - A)^{2} ]}} $$

(A-42)

$$ \tau_{R}^{MR - M*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{8C_{L} - 3\beta (\Delta - A)^{2} }} $$

(A-43)

Limitation $0 \le \tau_{M}^{MR - M*} + \tau_{R}^{MR - M*} < 1$ completes this section.

MR-R Model, manufacturer, and retailer hybrid collection: retailer Stackelberg

• Problem of manufacturer

given that the manufacturer profit function is incremental to the wholesale price, the wholesale price in this model will be as follows, which is the same as with the R-R Model (explained in “Appendix A” No. 2),

$$ \hat{W}^{MR - R} = \frac{{p^{MR - R} + C_{m} }}{2} $$

(A-44)

For the manufacturer’s collection rate, the second derivative of the manufacturer profit function is calculated due to the manufacturer’s collection rate as,

$$ \frac{{\partial \Pi_{M}^{MR - R} }}{{\partial \tau_{M}^{MR - R} }} = (\phi - \beta p)(\Delta - A) - 2C_{L} \tau_{M}^{MR - R} $$

(A-45)

$$ \frac{{\partial^{2} \Pi_{M}^{MR - R} }}{{\partial (\tau_{M}^{MR - R} )^{2} }} = - 2C_{L} $$

(A-46)

Given that $\frac{{\partial^{2} \Pi_{M}^{MR - R} }}{{\partial (\tau_{M}^{MR - R} )^{2} }} < 0$, the manufacturer profit function will be concave, and the manufacturer’s collection rate is as follows,

$$ \hat{\tau }_{M}^{MR - R} = \frac{(\phi - \beta p)(\Delta - A)}{{2C_{L} }} $$

(A-47)

• Problem of retailer

Considering the manufacturer’s solutions, the retailer profit function is

$$ \hat{\Pi }_{R}^{MR - R} = \frac{{(p - C_{m} )}}{2}(\phi - \beta p) + (\phi - \beta p)(b - A)\tau_{R}^{MR - R} - C_{L} (\tau_{R}^{MR - R} )^{2} $$

(A-48)

Now, to investigate the concavity of the retailer profit function due to the wholesale price and retailer’s collection rate, its Hessian matrix is formed as,

$$ \frac{{\partial \hat{\Pi }_{R}^{MR - R} }}{{\partial p^{MR - R} }} = \frac{{(\phi + \beta C_{m} )}}{2} - \beta p - \beta (b - A)\tau_{R}^{MR - R} $$

(A-49)

$$ \frac{{\partial \hat{\Pi }_{R}^{MR - R} }}{{\partial \tau_{R}^{MR - R} }} = (\phi - \beta p)(b - A) - 2C_{L} \tau_{R}^{MR - R} $$

(A-50)

$$ H(\hat{\Pi }_{R}^{MR - R} ) = \left[ {\begin{array}{*{20}c} { - \beta } & { - \beta (b - A)} \\ { - \beta (b - A)} & { - 2C_{L} } \\ \end{array} } \right] $$

(A-51)

If the above Hessian matrix is negative, the retailer profit function is concave. Thus, the retailer profit function will be concave with a unique optimal solution if

$$2C_{L} > \beta (b - A)^{2}$$

(A-52)

Now, let us obtain the retailer’s best reactions using the first-order condition as,

$$ \hat{p}^{MR - R} = \frac{{C_{L} (\phi + \beta C_{m} ) - \beta \phi (b - A)^{2} }}{{\beta \left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-53)

$$ \hat{\tau }_{R}^{MR - R} = \frac{{(\phi - \beta C_{m} )(b - A)}}{{2\left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-54)

Replacing $\hat{p}^{MR - R}$ in $\hat{W}^{MR - R}$ and $\hat{\tau }_{M}^{MR - R}$ equations give the wholesale price and manufacturer’s collection rate as,

$$ \hat{W}^{MR - R} = \frac{{C_{L} (\phi + 3\beta C_{m} ) - \beta (b - A)^{2} (\phi + \beta C_{m} )}}{{2\beta \left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-55)

$$ \hat{\tau }_{R}^{MR - R} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{2\left[ {2C_{L} - \beta (b - A)^{2} } \right]}} $$

(A-56)

The same as with the R-R Model in “Appendix A” and increase in b increases both the manufacturer’s collection rate and retailer’s collection rate and reduces both the retail price and wholesale price. The increased collection rates reduce manufacturing cost $\overline{C} = C_{m} - \Delta \tau$ and the reduced cost increases the demand for the product. The increased demand and reduced manufacturing cost increase profit. Thus, the manufacturer gives the entire saving resulted from the manufacturing to the retailer. Hence, $\frac{{\partial \Pi_{M}^{MR - R} }}{\partial b} > 0$ and $b = \Delta$.

Now, the optimal decisions of the manufacturer and retailer will be,

$$ W^{MR - R*} = \frac{{C_{L} (\phi + 3\beta C_{m} ) - \beta (\Delta - A)^{2} (\phi + \beta C_{m} )}}{{2\beta [2C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-57)

$$ \tau_{M}^{MR - R*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{2\left[ {2C_{L} - \beta (\Delta - A)^{2} } \right]}} $$

(A-58)

$$ p^{MR - R*} = \frac{{C_{L} (\phi + \beta C_{m} ) - \beta \phi (\Delta - A)^{2} }}{{\beta [2C_{L} - \beta (\Delta - A)^{2} ]}} $$

(A-59)

$$ \tau_{R}^{MR - R*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)}}{{2\left[ {2C_{L} - \beta (\Delta - A)^{2} } \right]}} $$

(A-60)

Limitation $0 \le \tau_{M}^{MR - R*} + \tau_{R}^{MR - R*} < 1$ completes this section.

Appendix C

M&R-M Model, manufacturer and retailer competitive collection: manufacturer Stackelberg

• Problem of retailer

We need to first investigate the retailer profit function concavity to obtain equilibrium retailer decisions. Thus, we have

$$ \frac{{\partial \Pi_{R}^{M\& R - M} }}{{\partial p^{M\& R - M} }} = (\phi + \beta W) - 2\beta p - \beta (b - A)\tau_{R}^{M\& R - M} $$

(A-61)

$$ \frac{{\partial \Pi_{R}^{M\& R - M} }}{{\partial \tau_{R}^{M\& R - M} }} = (\phi - \beta p)(b - A) - \frac{{2C_{L} \tau_{R}^{M\& R - M} }}{{1 - \alpha^{2} }} $$

(A-62)

To investigate the retailer profit function concavity, we need to form its Hessian matrix as,

$$ H(\Pi_{R}^{M\& R - M} ) = \left[ {\begin{array}{*{20}c} { - 2\beta } & { - \beta (b - A)} \\ { - \beta (b - A)} & { - \frac{{2C_{L} }}{{1 - \alpha^{2} }}} \\ \end{array} } \right] $$

(A-63)

For the retailer profit function to be concave, the Hessian matrix should be negative: i.e. its determinants should be negative and positive decussate and $\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0$. In this case, the retailer profit function will be concave compared to $p^{M\& R - M} , \, \tau_{R}^{M\& R - M}$ with a unique optimal solution if $4C_{L} > \beta (b - A)^{2} (1 - \alpha^{2} )$. Now, the retailer’s optimal decisions are obtained by using the first-order condition as,

$$ \hat{p}^{M\& R - M} = \frac{{2C_{L} (\phi + \beta W) - \beta \phi (b - A)^{2} (1 - \alpha^{2} )}}{{\beta \left[ {4C_{L} - \beta (b - A)^{2} (1 - \alpha^{2} )} \right]}} $$

(A-64)

$$ \hat{\tau }_{R}^{M\& R - M} = \frac{{(\phi - \beta W)(b - A)(1 - \alpha^{2} )}}{{4C_{L} - \beta (b - A)^{2} (1 - \alpha^{2} )}} $$

(A-65)

• Problem of manufacturer

Replacing $\hat{p}^{M\& R - M}$ and $\hat{\tau }_{M}^{M\& R - M}$ in the retailer profit function and considering $Y = 4C_{L} - \beta (b - A)^{2} (1 - \alpha^{2} )$ and $S = (b - A)(\Delta - b)$ gives the manufacturer profit function as

$$ \begin{gathered} \hat{\Pi }_{M}^{M\& R - M} = \frac{{2C_{L} (\phi - \beta W)}}{Y}\left[ {W - C_{m} + (\Delta - A)\tau_{M}^{M\& R - M} + \frac{{S(\phi - \beta W)(1 - \alpha^{2} )}}{Y}} \right] \hfill \\ \, - \frac{{C_{L} (\tau_{M}^{M\& R - M} )^{2} }}{{(1 - \alpha^{2} )}} - \frac{{\alpha C_{L} (\phi - \beta W)^{2} (b - A)^{2} (1 - \alpha^{2} )}}{{Y^{2} }} \hfill \\ \end{gathered} $$

(A-66)

$$ \begin{gathered} \frac{{\partial \hat{\Pi }_{M}^{M\& R - M} }}{{\partial W^{M\& R - M} }} = \frac{{2C_{L} }}{Y}\left[ {\phi + \beta C_{m} - 2\beta W - \beta (\Delta - A)\tau_{M}^{M\& R - M} - \frac{{2\beta S(1 - \alpha^{2} )(\phi - \beta W)}}{Y}} \right] \hfill \\ \, + \frac{{2\beta \alpha C_{L} (\phi - \beta W)(b - A)^{2} (1 - \alpha^{2} )}}{{Y^{2} }} \hfill \\ \end{gathered} $$

(A-67)

$$ \frac{{\partial \hat{\Pi }_{M}^{M\& R - M} }}{{\partial \tau_{M}^{M\& R - M} }} = \frac{{2C_{L} (\phi - \beta W)(\Delta - A)}}{Y} - \frac{{2C_{L} \tau_{M}^{M\& R - M} }}{{(1 - \alpha^{2} )}} $$

(A-68)

For the manufacturer problem to have a unique optimal solution, the manufacturer profit function has to be concave due to the wholesale price and manufacturer’s collection rate. Thus, we form the Hessian matrix of the manufacturer’s profit as,

$$ H(\hat{\Pi }_{M}^{M\& R - M} ) = \left[ {\begin{array}{*{20}c} {\frac{{ - 4\beta C_{L} }}{Y} + \frac{{4C_{L} \beta^{2} S(1 - \alpha^{2} )}}{{Y^{2} }} - \frac{{2\beta^{2} \alpha C_{L} (b - A)^{2} (1 - \alpha^{2} )}}{{Y^{2} }}} & { - \frac{{2C_{L} \beta (\Delta - A)}}{Y}} \\ { - \frac{{2C_{L} \beta (\Delta - A)}}{Y}} & {\frac{{ - 2C_{L} }}{{(1 - \alpha^{2} )}}} \\ \end{array} } \right] $$

(A-69)

If the Hessian matrix is negative and the manufacturer profit function is concave, then If $8C_{L} > \beta (1 - \alpha^{2} )\left[ {2S + (b - A)^{2} (2 - \alpha ) + (\Delta - A)^{2} } \right]$, the manufacturer’s optimal decisions will be as follows,

$$ W^{M\& R - M*} = \frac{{4C_{L} (\phi + \beta C_{m} ) - \beta \phi (\Delta - A)^{2} (1 - \alpha^{2} )(2 - \alpha ) - \beta^{2} C_{m} (\Delta - A)^{2} (1 - \alpha^{2} )}}{{\beta [8C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(3 - \alpha )]}} $$

(A-70)

$$ \tau_{M}^{M\& R - M*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)(1 - \alpha^{2} )}}{{8C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(3 - \alpha )}} $$

(A-71)

As same as with the previous explanations, $\frac{{\partial \Pi_{M}^{M\& R - R} }}{\partial b} > 0$ and $b = \Delta$.

Replacing $W^{MR - M*}$ in $\hat{p}^{M\& R - M}$ and $\hat{\tau }_{M}^{M\& R - M}$ equations give the optimal retail price and retailer’s collection rate as,

$$ p^{M\& R - M*} = \frac{\begin{gathered} 2C_{L} \left[ {4C_{L} (3\phi + \beta C_{m} ) - \beta \phi (\Delta - A)^{2} (1 - \alpha^{2} )(5 - 2\alpha ) - \beta^{2} C_{m} (\Delta - A)^{2} (1 - \alpha^{2} )} \right] \hfill \\ - \beta \phi (\Delta - A)^{2} (1 - \alpha^{2} )\left[ {8C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(3 - \alpha )} \right] \hfill \\ \end{gathered} }{{\beta [4C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )][8C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(3 - \alpha )]}} $$

(A-72)

$$ \tau_{R}^{M\& R - M*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)(1 - \alpha^{2} )}}{{8C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(3 - \alpha )}} $$

(A-73)

Limitation $0 \le \tau_{M}^{M\& R - M*} + \tau_{R}^{M\& R - M*} < 1$ completes this section.

M&R-R Model, manufacturer, and retailer competitive collection: retailer Stackelberg

• Problem of manufacturer

The same approach as with the previous retailer Stackelberg models is employed in this model. The wholesale price is as follows

$$ \hat{W}^{M\& R - R} = \frac{{p^{M\& R - R} + C_{m} }}{2} $$

(A-74)

Since concavity plays an important role in obtaining optimal decisions, the manufacturer profit function concavity according to the manufacturer’s collection rate is investigated.

$$ \frac{{\partial \Pi_{M}^{M\& R - R} }}{{\partial \tau_{M}^{M\& R - R} }} = (\phi - \beta p)(\Delta - A) - \frac{{2C_{L} \tau_{M}^{M\& R - R} }}{{(1 - \alpha^{2} )}} $$

(A-75)

$$ \frac{{\partial^{2} \Pi_{M}^{M\& R - R} }}{{\partial (\tau_{M}^{M\& R - R} )^{2} }} = \frac{{ - 2C_{L} }}{{1 - \alpha^{2} }} < 0 $$

(A-76)

$\frac{{\partial^{2} \Pi_{M}^{M\& R - R} }}{{\partial (\tau_{M}^{M\& R - R} )^{2} }} < 0$ shows that the manufacturer profit function is concave due to the manufacturer’s collection rate. The manufacturer’s collection rate is,

$$ \hat{\tau }_{M}^{M\& R - R} = \frac{{(\phi - \beta p)(\Delta - A)(1 - \alpha^{2} )}}{{2C_{L} }} $$

(A-77)

• Problem of retailer

given the manufacturer solutions, the retailer profit function will be as follows,

$$ \begin{aligned} \hat{\Pi }_{R}^{{M\& R - R}} = & \frac{{(p - C_{m} )}}{2}(\phi - \beta p) + (\phi - \beta p)(b - A)\tau _{R}^{{M\& R - R}} - \frac{{C_{L} (\tau _{R}^{{M\& R - R}} )^{2} }}{{(1 - \alpha ^{2} )}} \\ {\text{ }} & - \frac{{\alpha (\phi - \beta p)^{2} (\Delta - A)^{2} (1 - \alpha ^{2} )}}{{4C_{L} }} \\ \end{aligned} $$

(A-78)

Since concavity plays an important role in obtaining optimal decisions, its Hessian matrix is formed as follows to investigate the retailer profit function concavity due to the retail price and retailer’s collection rate:

$$ \frac{{\partial \hat{\Pi }_{R}^{M\& R - R} }}{{\partial p^{M\& R - R} }} = \frac{{(\phi + \beta C_{m} )}}{2} - \beta p - \beta (b - A)\tau_{R}^{M\& R - R} + \frac{{\beta \alpha (\phi - \beta p)(1 - \alpha^{2} )(\Delta - A)^{2} }}{{2C_{L} }} $$

(A-79)

$$ \frac{{\partial \hat{\Pi }_{R}^{M\& R - R} }}{{\partial \tau_{R}^{M\& R - R} }} = (\phi - \beta p)(b - A) - \frac{{2C_{L} \tau_{R}^{M\& R - R} }}{{(1 - \alpha^{2} )}} $$

(A-80)

$$ H(\hat{\Pi }_{R}^{M\& R - R} ) = \left[ {\begin{array}{*{20}c} {\frac{{ - 2C_{L} \beta - \beta^{2} \alpha (1 - \alpha^{2} )(\Delta - A)^{2} }}{{2C_{L} }}} & { - \beta (b - A)} \\ { - \beta (b - A)} & {\frac{{ - 2C_{L} }}{{(1 - \alpha^{2} )}}} \\ \end{array} } \right] $$

(A-81)

If the determinants of the Hessian matrix are negative and positive decussate (i.e.$\left| {H_{1} } \right| < 0, \, \left| {H_{2} } \right| > 0$), the retailer profit function is concave. Thus, the retailer profit function will be concave with a unique optimal solution if

$$ 2C_{L} > \beta (1 - \alpha^{2} )\left[ {(b - A)^{2} - \alpha (\Delta - A)^{2} } \right] $$

(A-82)

Now, the following equations are solved using the first-order condition, obtaining the retailer’s best reactions.

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\partial \Pi_{R}^{M\& R - R} }}{{\partial p^{M\& R - R} }} = 0} \\ {\frac{{\partial \Pi_{R}^{M\& R - R} }}{{\partial \tau_{R}^{M\& R - R} }} = 0} \\ \end{array} } \right. $$

(A-83)

$$ p^{M\& R - R*} = \frac{{C_{L} (\phi + \beta C_{m} ) - \beta \phi (\Delta - A)^{2} (1 - \alpha^{2} )(1 - \alpha )}}{{\beta [2C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(1 - \alpha )]}} $$

(A-84)

$$ \tau_{R}^{M\& R - R*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)(1 - \alpha^{2} )}}{{2\left[ {2C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(1 - \alpha )} \right]}} $$

(A-85)

Replacing $p^{M\& R - R*}$ in $\hat{W}^{M\& R - R}$ and $\hat{\tau }_{M}^{M\& R - R}$ equations give the optimal wholesale price and manufacturer’s collection rate as

$$ W^{M\& R - R*} = \frac{{C_{L} (\phi + 3\beta C_{m} ) - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(1 - \alpha )(\phi + \beta C_{m} )}}{{2\beta [2C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(1 - \alpha )]}} $$

(A-86)

$$ \tau_{M}^{M\& R - R*} = \frac{{(\phi - \beta C_{m} )(\Delta - A)(1 - \alpha^{2} )}}{{2\left[ {2C_{L} - \beta (\Delta - A)^{2} (1 - \alpha^{2} )(1 - \alpha )} \right]}} $$

(A-87)

The same with the previous models, this model gives the entire saving resulted from remanufacturing $\Delta$ to the retailer, and thus $\frac{{\partial \Pi_{M}^{M\& R - R} }}{\partial b} > 0$ and $b = \Delta$.

Limitation $0 \le \tau_{M}^{M\& R - R*} + \tau_{R}^{M\& R - R*} < 1$ completes the proof of this section.