Emission reduction and coordination of a dynamic supply chain with green reputation

Abstract

The public’s increasing concern for carbon emissions promotes supply chain operations toward sustainability. This study investigates a dynamic supply chain consisting of a manufacturer and a retailer, wherein a product marked with emissions is produced and sold to consumers. A Stackelberg differential game is modeled, and the equilibrium pricing and emission reduction solutions are compared between integrated and decentralized channel settings. A two-part tariff contract is further proposed to improve channel performance. The numerical analysis illustrates that the emission reduction level, green reputation, demand, and entire profit of the supply chain are larger in the integrated setting than the counterparts in the decentralized setting. However, the relationship between the two channels in terms of retail price depends on unit carbon tax. In addition, the two-part tariff contract can perfectly achieve channel coordination. Results also indicate that firms can benefit from increasing the effect of green reputation on demand.

Appendices

Appendix A

Proof of Proposition 1

Let $V^{I}$ represent the value function of an integrated setting. Thus, the Hamilton–Jacobi–Bellman (HJB) equation is expressed as:

$$\rho V^{I} = \mathop {max}\limits_{p,\tau } \left\{ {p \cdot \left( {\alpha - \beta p - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) - s\left( {1 - \tau } \right)E_{0} \cdot \left( {\alpha - \beta p - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) - \frac{k}{2}\tau^{2} + \frac{{\partial V^{I} }}{\partial G}\left( {\theta \tau - \delta G} \right)} \right\}$$

(A.1)

Using the first-order condition to maximize the right-hand side of the above HJB equation, we can obtain

$$2\beta p + \left( {\beta s - \gamma } \right)E_{0} \tau = \eta G + \alpha + \left( {\beta s - \gamma } \right)E_{0}$$

(A.2)

$$\left( {\beta s - \gamma } \right)E_{0} p + \left( {k - 2s\gamma E_{0}^{2} } \right)\tau = \eta sE_{0} G + sE_{0} \left( {\alpha - 2\gamma E_{0} } \right) + \frac{{\partial V^{I} }}{\partial G}\theta$$

(A.3)

Given the simultaneous Equations (A.1) and (A.2), we can obtain the retail price and the emission reduction level as follows:

$$p = \frac{{\eta k - \eta sE_{0}^{2} \left( {\beta s + \gamma } \right)}}{{A_{1} }}G - \frac{{\theta E_{0} \left( {\beta s - \gamma } \right)}}{{A_{1} }}\frac{{\partial V^{I} }}{\partial G} + \frac{{k\alpha + kE_{0} \left( {\beta s - \gamma } \right) - \alpha sE_{0}^{2} \left( {\beta s + \gamma } \right)}}{{A_{1} }}$$

(A.4)

$$\tau = \frac{{\eta A_{0} }}{{A_{1} }}G + \frac{2\beta \theta }{{A_{1} }}\frac{{\partial V^{I} }}{\partial G} + \frac{{\alpha A_{0} - A_{0}^{2} }}{{A_{1} }}$$

(A.5)

Substituting Equations (A.4) and (A.5) into the right-hand side of (A.1) yields

$$\rho V^{I} = \frac{{k\eta^{2} }}{{2A_{1} }}G^{2} + \frac{{\eta \theta A_{0} - \delta A_{1} }}{{A_{1} }}G \cdot \frac{{\partial V^{I} }}{\partial G} + \frac{{k\alpha \eta - k\eta A_{0} }}{{A_{1} }}G + \frac{{\beta \theta^{2} }}{{A_{1} }}\left( {\frac{{\partial V^{I} }}{\partial G}} \right)^{2} + \frac{{\alpha \theta A_{0} - \theta A_{0}^{2} }}{{A_{1} }}\frac{{\partial V^{I} }}{\partial G} + \frac{{k\left( {\alpha - A_{0} } \right)^{2} }}{{2A_{1} }}$$

(A.6)

We develop the following quadratic value function:

$$V^{I} \left( G \right) = \frac{{X_{1} }}{2}G^{2} + X_{2} G + X_{3}$$

(A.7)

where $X_{1}$, $X_{2}$, and $X_{3}$ are the coefficients to be determined. From Function (A.7), we have

$$\frac{{\partial V^{I} }}{\partial G} = X_{1} G + X_{2}$$

(A.8)

Substituting (A.7) and (A.8) into (A.6) yields

$$\rho \left( {\frac{{X_{1} }}{2}G^{2} + X_{2} G + X_{3} } \right) = \frac{{k\eta^{2} }}{{2A_{1} }}G^{2} + \frac{{\eta \theta A_{0} - \delta A_{1} }}{{A_{1} }}\left( {X_{1} G^{2} + X_{2} G} \right) + \frac{{k\eta \left( {\alpha - A_{0} } \right)}}{{A_{1} }}G + \frac{{\beta \theta^{2} }}{{A_{1} }}\left( {X_{1}^{2} G^{2} + 2X_{1} X_{2} G + X_{2}^{2} } \right) + \frac{{\theta A_{0} \left( {\alpha - A_{0} } \right)}}{{A_{1} }}\left( {X_{1} G + X_{2} } \right) + \frac{{k\left( {\alpha - A_{0} } \right)^{2} }}{{2A_{1} }}$$

(A.9)

Let the corresponding coefficients of $G^{2}$ on both sides of equation (A.9) be equal. Thus, we can obtain

$$2\beta \theta^{2} \cdot X_{1}^{2} + \left( {2\eta \theta A_{0} - \left( {\rho + 2\delta } \right)A_{1} } \right)X_{1} + k\eta^{2} = 0$$

(A.10)

Solving Equation (A.10) yields

$$X_{1} = \frac{{ - A_{2} - \Delta_{1} }}{{4\beta \theta^{2} }}$$

(A.11)

where $\Delta_{1} \ge 0$ is required to guarantee the existence of the solution. When $X_{1}$ takes a large root, the green reputation level will not converge to a steady-state value. Thus, the large root is abandoned.

Similarly, $X_{2}$ and $X_{3}$ are obtained as the following:

$$X_{2} = \frac{{\left( {\alpha - A_{0} } \right)\left( {2\eta \theta A_{1} + \left( {\rho + 2\delta } \right)A_{0} A_{1} - \Delta_{1} A_{0} } \right)}}{{2\beta \theta \left( {\rho A_{1} + \Delta_{1} } \right)}}$$

(A.12)

$$X_{3} = \frac{{\left( {\alpha - A_{0} } \right)^{2} \left\{ {\left[ {2\eta \theta A_{1} + \left( {\rho + 2\delta } \right)A_{0} A_{1} - \Delta_{1} A_{0} } \right]\left[ {2\eta \theta A_{1} + \left( {3\rho + 2\delta } \right)A_{0} A_{1} + \Delta_{1} A_{0} } \right] + 2\beta k\left( {\rho A_{1} + \Delta_{1} } \right)^{2} } \right\}}}{{4\beta \rho A_{1} \left( {\rho A_{1} + \Delta_{1} } \right)^{2} }}$$

(A.13)

Proof of Corollary1

By substituting Eq. (9) into (1), we obtain the following differential equation:

$$\dot{G}\left( t \right) = \frac{{\rho A_{1} - \Delta_{1} }}{{2A_{1} }}G + \frac{{2\theta \left( {\alpha - A_{0} } \right)\left( {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right)}}{{\rho A_{1} + \Delta_{1} }}$$

(A.14)

Given that $G\left( 0 \right) = G_{0}$, solving Equation (A.14) yields (10), where $G_{\infty }^{I}$ can be obtained as follows:

$$G_{\infty }^{I} = \frac{{4\theta \left( {\alpha - A_{0} } \right)A_{1} \left( {\eta \theta + \left( {\rho + {\updelta }} \right)A_{0} } \right)}}{{\left( {\Delta_{1} + \rho A_{1} } \right)\left( {\Delta_{1} - \rho A_{1} } \right)}}$$

(A.15)

By substituting Equations (A.15) and (10) into (8) and (9), we can obtain Eqs. (11) and (12), where $p_{\infty }^{I}$ and $\tau_{\infty }^{I}$ can be obtained as follows:

$$p_{\infty }^{I} = \frac{{k\alpha + kE_{0} \left( {\beta s - \gamma } \right) - \alpha sE_{0} A_{0} - \theta E_{0} \left( {\beta s - \gamma } \right)X_{2} + \left( {\eta k - \eta sE_{0} A_{0} - \theta E_{0} \left( {\beta s - \gamma } \right)X_{1} } \right)G_{\infty }^{I} }}{{A_{1} }}$$

(A.16)

$$\tau_{\infty }^{I} = \frac{{2\beta \theta X_{2} + \alpha A_{0} - A_{0}^{2} + \left( {\eta A_{0} + 2\beta \theta X_{1} } \right)G_{\infty }^{I} }}{{A_{1} }}$$

(A.17)

Proof of Proposition 2

By substituting Eq. (10) into (8) and (9), we can obtain Eqs. (11) and (12).

Proof of Corollary 2

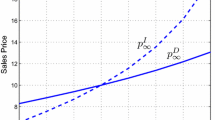
Proposition 2 shows that the monotonicity of retail price relates to $G_{0}$ and $G_{\infty }$ when $\frac{{\left( {\eta k - \eta sE_{0} A_{0} - \theta E_{0} \left( {\beta s - \gamma } \right)X_{1} } \right)}}{{A_{1} }} > 0$. In particular, when $G_{0} > G_{\infty }^{I}$, the retail price decreases as time increases. Therefore, the skimming pricing strategy should be adopted. When $G_{0} < G_{\infty }^{I}$, the retail price increase as time increases, which requires the adoption of the penetration pricing strategy.

Given that $0 < {\upgamma } < \frac{\alpha }{{E_{0} - \beta s}}$, which can ensure $G_{\infty }^{I} > 0$, we have $0 < G_{\infty }^{I} < \frac{{\theta \left( {\alpha - \beta sE_{0} } \right)\left[ {\eta \theta + \beta sE_{0} \left( {\rho + \delta } \right)} \right]}}{{\delta \left( {\rho + \delta } \right)\left( {2\beta k - \beta^{2} s^{2} E_{0}^{2} } \right) - \eta \theta \left[ {\eta \theta + \beta sE_{0} \left( {\rho + 2\delta } \right)} \right]}}$.

If $G_{0} > \frac{{\theta \left( {\alpha - \beta sE_{0} } \right)\left[ {\eta \theta + \beta sE_{0} \left( {\rho + \delta } \right)} \right]}}{{\delta \left( {\rho + \delta } \right)\left( {2\beta k - \beta^{2} s^{2} E_{0}^{2} } \right) - \eta \theta \left[ {\eta \theta + \beta sE_{0} \left( {\rho + 2\delta } \right)} \right]}}$, which indicates that $G_{0} > G_{\infty }^{I}$, then firms should adopt the skimming pricing strategy.

If $0 < G_{0} < \frac{{\theta \left( {\alpha - \beta sE_{0} } \right)\left[ {\eta \theta + \beta sE_{0} \left( {\rho + \delta } \right)} \right]}}{{\delta \left( {\rho + \delta } \right)\left( {2\beta k - \beta^{2} s^{2} E_{0}^{2} } \right) - \eta \theta \left[ {\eta \theta + \beta sE_{0} \left( {\rho + 2\delta } \right)} \right]}}$, a $\tilde{\gamma }$ that satisfies $G_{0} = G_{\infty }$ exists. When $0 < {\upgamma } < { }\tilde{\gamma }$, which means that $G_{0} < G_{\infty }^{I}$, the penetration pricing strategy should be adopted. When $\tilde{\gamma } < {\upgamma } < {\upalpha }/E_{0} - \beta s$, which indicates that $G_{0} > G_{\infty }^{I}$, the skimming pricing strategy should be adopted.

Proof of Proposition 3

Let $V_{r}^{D}$ and $V_{m}^{D}$ represent the value functions of the retailer and the manufacturer in the decentralized setting. Thus, the HJB equations are expressed as:

$$\rho V_{r}^{D} = \mathop {max}\limits_{p} \left\{ {\left( {p - w} \right) \cdot \left( {\alpha - \beta p - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) + \frac{{\partial V_{r}^{D} }}{\partial G}\left( {\theta \tau - \delta G} \right)} \right\}$$

(A.18)

$$\rho V_{m}^{D} = \mathop {max}\limits_{w,\tau } \left\{ {w \cdot \left( {\alpha - \beta p - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) - s\left( {1 - \tau } \right)E_{0} \cdot \left( {\alpha - \beta p - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) - \frac{k}{2}\tau^{2} + \frac{{\partial V_{m}^{D} }}{\partial G}\left( {\theta \tau - \delta G} \right)} \right\}$$

(A.19)

By using the first-order condition to maximize the right-hand side of Equation (A.18), we can obtain

$$p = \frac{w}{2} + \frac{{\gamma E_{0} }}{2\beta }\tau + \frac{\eta }{2\beta }G + \frac{{\alpha - \gamma E_{0} }}{2\beta }$$

(A.20)

Substituting Equation (A.20) into the right-hand side of Equation (A.19) yields

$$\rho V_{m}^{D} = \mathop {max}\limits_{w,\tau } \left\{ {\frac{w}{2} \cdot \left( {\alpha - \beta w - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) - \frac{s}{2}\left( {1 - \tau } \right)E_{0} \cdot \left( {\alpha - \beta w - \gamma \left( {1 - \tau } \right)E_{0} + \eta G} \right) - \frac{k}{2}\tau^{2} + \frac{{\partial V_{m}^{D} }}{\partial G}\left( {\theta \tau - \delta G} \right)} \right\}$$

(A.21)

Using the first-order condition to solve the right-hand side of Equation (A.21) with respect to $w$ and $\tau$, we obtain the following:

$$2\beta w + \left( {\beta s - \gamma } \right)E_{0} \tau = \eta G + \alpha + \left( {\beta s - \gamma } \right)E_{0}$$

(A.22)

$$\left( {\beta s - \gamma } \right)E_{0} w + 2\left( {k - s\gamma E_{0}^{2} } \right)\tau = sE_{0} \eta G + \alpha sE_{0} - 2s\gamma E_{0}^{2} + 2\theta \frac{{\partial V_{m}^{D} }}{\partial G}$$

(A.23)

Given the simultaneous Equations (A.22) and (A.23), we can obtain the wholesale price and the emission reduction level as follows:

$$w = \frac{{2\eta k - \eta sE_{0}^{2} \left( {\beta s + \gamma } \right)}}{{A_{3} }}G - \frac{{2\theta E_{0} \left( {\beta s - \gamma } \right)}}{{A_{3} }}\frac{{\partial V_{m}^{D} }}{\partial G} + \frac{{2k\alpha + 2kE_{0} \left( {\beta s - \gamma } \right) - \alpha sE_{0}^{2} \left( {\beta s + \gamma } \right)}}{{A_{3} }}$$

(A.24)

$$\tau = \frac{{\eta A_{0} }}{{A_{3} }}G + \frac{4\beta \theta }{{A_{3} }}\frac{{\partial V_{m}^{D} }}{\partial G} + \frac{{\alpha A_{0} - A_{0}^{2} }}{{A_{3} }}$$

(A.25)

Substituting Equations (A.24) and (A.25) into the right-hand side of Equation (A.21) yields

$$\begin{aligned} \rho V_{m}^{D} = & \frac{{k\eta ^{2} }}{{2A_{3} }}G^{2} + \frac{{\eta \theta A_{0} - \delta A_{3} }}{{A_{3} }}G \cdot \frac{{\partial V_{m}^{D} }}{{\partial G}} + \frac{{k\alpha \eta - k\eta A_{0} }}{{A_{3} }}G \\ & + \frac{{2\beta \theta ^{2} }}{{A_{3} }}\left( {\frac{{\partial V_{m}^{D} }}{{\partial G}}} \right)^{2} + \frac{{\alpha \theta A_{0} - \theta A_{0} ^{2} }}{{A_{3} }}\frac{{\partial V_{m}^{D} }}{{\partial G}} + \frac{{k\alpha ^{2} - 2k\alpha A_{0} + kA_{0} ^{2} }}{{2A_{3} }} \\ \end{aligned}$$

(A.26)

We conjecture the manufacturer’s value function as a quadratic form, which is expressed as follows:

$$V_{m}^{D} \left( G \right) = \frac{{Y_{1} }}{2}G^{2} + Y_{2} G + Y_{3}$$

(A.27)

where $Y_{1}$, $Y_{2}$, and $Y_{3}$ are the coefficients to be determined. From Function (A.27), we have

$$\frac{{\partial V_{m}^{D} }}{\partial G} = Y_{1} G + Y_{2}$$

(A.28)

By substituting (A.27) and (A.28) into (A.26) and letting the corresponding coefficients of $G^{2}$ on both sides of the equation be equal, we can obtain

$$4\beta \theta^{2} \cdot Y_{1}^{2} + \left( {2\eta \theta A_{0} - \left( {\rho + 2\delta } \right)A_{3} } \right) \cdot Y_{1} + k\eta^{2} = 0$$

(A.29)

Solving Equation (A.29) yields

$$Y_{1} = \frac{{ - A_{4} - \Delta_{2} }}{{8\beta \theta^{2} }}$$

(A.30)

where $\Delta_{2} \ge 0$ is required to guarantee the existence of the solution. When $Y_{1}$ takes a large root, the green reputation level will not converge to a steady-state value. Thus, the large root is abandoned.

Similarly, $Y_{2}$ and $Y_{3}$ are obtained as the following:

$$Y_{2} = \frac{{\left( {\alpha - A_{0} } \right)\left( {2\eta \theta A_{3} + \left( {\rho + 2\delta } \right)A_{0} A_{3} - A_{0} \Delta_{2} } \right)}}{{4\beta \theta \left( {\rho A_{3} + \Delta_{2} } \right)}} = \frac{{\left( {\alpha - A_{0} } \right)\left( {8k\beta \theta \eta - A_{0} \left( {A_{4} + \Delta_{2} } \right)} \right)}}{{4\beta \theta \left( {\rho A_{3} + \Delta_{2} } \right)}}$$

(A.31)

$$\begin{aligned} Y_{3} = & \frac{{\left( {\alpha - A_{0} } \right)^{2} \left( {8k\beta \theta \eta - A_{0} \left( {A_{4} + \Delta _{2} } \right)} \right)^{2} }}{{8\beta \rho A_{3} \left( {\rho A_{3} + \Delta _{2} } \right)^{2} }} \\ & + \frac{{A_{0} \left( {\alpha - A_{0} } \right)^{2} \left( {8k\beta \theta \eta - A_{0} \left( {A_{4} + \Delta _{2} } \right)} \right)}}{{4\beta \rho A_{3} \left( {\rho A_{3} + \Delta _{2} } \right)}} \\ & + \frac{{k\alpha ^{2} - 2k\alpha A_{0} + kA_{0} ^{2} }}{{2\rho A_{3} }} \\ \end{aligned}$$

(A.32)

Substituting Equations (A.20), (A.24), and (A.25) into (A.18) yields

$$\begin{aligned} \rho V_{r}^{D} = & \frac{{\beta \left( {k\eta + \theta A_{0} Y_{1} } \right)^{2} }}{{A_{3}^{2} }}G^{2} + \frac{{\rho A_{3} - \Delta_{2} }}{{2A_{3} }}G \cdot \frac{{\partial V_{r}^{D} }}{\partial G} + \frac{{2\beta \left( {k\eta + \theta A_{0} Y_{1} } \right)\left( {k\alpha - kA_{0} + \theta A_{0} Y_{2} } \right)}}{{A_{3}^{2} }}G \\ & + \frac{{\theta \left( {4\beta \theta Y_{2} + \alpha A_{0} - A_{0}^{2} } \right)}}{{A_{3} }}\frac{{\partial V_{r}^{D} }}{\partial G} + { }\frac{{\beta \left( {k\alpha - kA_{0} + \theta A_{0} Y_{2} } \right)^{2} }}{{A_{3}^{2} }} \\ \end{aligned}$$

(A.33)

Similarly, the retailer’s value function is conjectured as follows:

$$V_{r}^{D} \left( G \right) = \frac{{Z_{1} }}{2}G^{2} + Z_{2} G + Z_{3}$$

(A.34)

where $Z_{1}$, $Z_{2}$ and $Z_{3}$ are the coefficients to be determined. From Function (A.34), we have

$$\frac{{\partial V_{r}^{D} }}{\partial G} = Z_{1} G + Z_{2}$$

(A.35)

By substituting (A.34) and (A.35) into (A.33) and letting the corresponding coefficients of $G^{2}$ on both sides of the equation be equal, we can obtain

$$\left( {\rho A_{3}^{2} - \Delta_{2} A_{3} } \right)Z_{1}^{2} - \rho A_{3}^{2} Z_{1} + 2\beta \left( {k\eta + \theta A_{0} Y_{1} } \right)^{2} = 0$$

(A.36)

Solving Equation (A.36) yields

$$Z_{1} = \frac{{\rho A_{3}^{2} - {\Delta }_{3} }}{{2A_{3} \left( {\rho A_{3} - \Delta_{2} } \right)}}$$

(A.37)

where $\Delta_{3} \ge 0$ is required to guarantee the existence of the solution. When $Z_{1}$ takes a large root, the green reputation level will not converge to a steady-state value. Thus, the large root is abandoned.

Similarly, $Z_{2}$ and $Z_{3}$ are obtained as the following:

$$Z_{2} = \frac{{4\beta B_{1} B_{2} + 2\theta A_{3} B_{3} Z_{1} }}{{A_{3} \left( {\rho A_{3} + \Delta_{2} } \right)}}$$

(A.38)

$$Z_{3} = \frac{{\theta A_{3} B_{3} Z_{2} + \beta B_{2}^{2} }}{{\rho A_{3}^{2} }}$$

(A.39)

Proof of Corollary 3

Based on Eqs. (14) and (15) in proposition 3, Corollary 3 can easily be obtained.

Proof of Proposition 4

By substituting Eq. (16) into (1), we obtain the following differential equation:

$$\dot{G}\left( t \right) = \frac{{\rho A_{3} - \Delta_{2} }}{{2A_{3} }}G + \frac{{2\theta \left( {\alpha - A_{0} } \right)\left( {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right)}}{{\rho A_{3} + \Delta_{2} }}$$

(A.40)

Given that $G\left( 0 \right) = G_{0}$, solving Equation (A.40) yields (17), where $G_{\infty }^{D}$ can be obtained as follows:

$$G_{\infty }^{D} = \frac{{4\theta \left( {\alpha - A_{0} } \right)A_{3} \left( {\eta \theta + \left( {\rho + {\updelta }} \right)A_{0} } \right)}}{{\left( {\Delta_{2} + \rho A_{3} } \right)\left( {\Delta_{2} - \rho A_{3} } \right)}}$$

(A.41)

By substituting Equations (A.41) and (17) into (14)–(16), we can obtain Eqs. (18)–(20), where $p_{\infty }^{D} , w_{\infty }^{D}$, and $\tau_{\infty }^{D}$ can be also obtained as follows:

$$p_{\infty }^{D} = \frac{{kE_{0} \left( {\beta s - 3\gamma } \right) + 3k\alpha - \alpha sE_{0} A_{0} - \theta E_{0} \left( {\beta s - 3\gamma } \right)Y_{2} + \left( {3\eta k - \eta sE_{0} A_{0} - \theta E_{0} \left( {\beta s - 3\gamma } \right)Y_{1} } \right)G_{\infty }^{D} }}{{A_{3} }}$$

(A.42)

$$w_{\infty }^{D} = \frac{{2k\alpha + 2kE_{0} \left( {\beta s - \gamma } \right) - \alpha sE_{0} A_{0} - 2\theta E_{0} \left( {\beta s - \gamma } \right)Y_{2} + \left( {2\eta k - \eta sE_{0} A_{0} - 2\theta E_{0} \left( {\beta s - \gamma } \right)Y_{1} } \right)G_{\infty }^{D} }}{{A_{3} }}$$

(A.43)

$$\tau_{\infty }^{D} = \frac{{4\beta \theta Y_{2} + \alpha A_{0} - A_{0}^{2} + \left( {\eta A_{0} + 4\beta \theta Y_{1} } \right)G_{\infty }^{D} }}{{A_{3} }}$$

(A.44)

Proof of Corollary 4

Simplifying Equations (A.15) and (A.41) yields

$$G_{\infty }^{I} = \frac{{\theta \left( {\alpha - A_{0} } \right)\left[ {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right]}}{{\delta \left( {\rho + \delta } \right)\left( {2\beta k - A_{0}^{2} } \right) - \eta \theta \left[ {\eta \theta + \left( {\rho + 2\delta } \right)A_{0} } \right]}}$$

(A.45)

$$G_{\infty }^{D} = \frac{{\theta \left( {\alpha - A_{0} } \right)\left[ {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right]}}{{\delta \left( {\rho + \delta } \right)\left( {4\beta k - A_{0}^{2} } \right) - \eta \theta \left[ {\eta \theta + \left( {\rho + 2\delta } \right)A_{0} } \right]}}$$

(A.46)

we can obtain $G_{\infty }^{I} > G_{\infty }^{D}$.

Substituting Equations (A.45) and (A.46) into (A.17) and (A.44) yields

$$\tau_{\infty }^{I} = \frac{{4\delta A_{1} \left( {\alpha - A_{0} } \right)\left[ {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right]}}{{\vartriangle_{1}^{2} - \rho^{2} A_{1}^{2} }} = \frac{\delta }{\theta }G_{\infty }^{I}$$

(A.47)

$$\tau_{\infty }^{D} = \frac{{4\delta A_{3} \left( {\alpha - A_{0} } \right)\left[ {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right]}}{{\vartriangle_{2}^{2} - \rho^{2} A_{3}^{2} }} = \frac{\delta }{\theta }G_{\infty }^{D}$$

(A.48)

$$\tau_{\infty }^{I} - \tau_{\infty }^{D} = \frac{\delta }{\theta }\left( {G_{\infty }^{I} - G_{\infty }^{D} } \right) > 0$$

(A.49)

thereby obtaining $\tau_{\infty }^{I} > \tau_{\infty }^{D}$.

Proof of Proposition 5

We let $V_{r}^{C}$ and $V^{C}$ represent the retailer’s and the manufacturer’s value functions of in coordination. The HJB equation of the retailer is provided by

$$\rho V_{r}^{C} = \mathop {max}\limits_{p} \left\{ {\left( {p\left( t \right) - s\left( {1 - \tau } \right)E_{0} } \right) \cdot D\left( t \right) - F + \frac{{\partial V_{r}^{C} }}{\partial G}\left( {\theta \tau - \delta G} \right)} \right\}$$

(A.50)

By using the first-order condition to maximize the right-hand side of Equation (A.50), we can obtain

$$p^{c} = \frac{{\alpha - \gamma \left( {1 - \tau } \right)E_{0} + \eta G + \beta s\left( {1 - \tau } \right)E_{0} }}{2\beta }$$

(A.51)

The optimal problem of the manufacturer is given by

$$\mathop {\max }\limits_{{\tau \left( \cdot \right)}} \int\limits_{0}^{\infty } {e^{{ - \rho t}} \left( {\left( {p\left( t \right) - s\left( {1 - \tau \left( t \right)} \right)E_{0} } \right) \cdot D\left( t \right) - \frac{k}{2}\tau ^{2} \left( t \right)} \right)dt}$$

(A.52)

The related HJB equation is

$$\rho V^{c} = \mathop {max}\limits_{\tau } \left\{ {\left( {p\left( t \right) - s\left( {1 - \tau } \right)E_{0} } \right) \cdot D\left( t \right) - \frac{k}{2}\tau^{2} \left( t \right) + \frac{{\partial V^{c} }}{\partial G}\left( {\theta \tau - \delta G} \right)} \right\}$$

(A.53)

Substituting Equation (A.51) into (A.53) to maximize the right-hand side of Equation (A.53) with respect to $\tau$ yields

$$\tau^{c} = \frac{{\eta A_{0} }}{{A_{1} }}G + \frac{2\beta \theta }{{A_{1} }}\frac{{\partial V^{c} }}{\partial G} + \frac{{\alpha A_{0} - A_{0}^{2} }}{{A_{1} }}$$

(A.54)

We conjecture quadratic value functions as follows:

$$V_{r}^{C} \left( G \right) = \frac{{N_{1} }}{2}G^{2} + N_{2} G + N_{3}$$

(A.55)

$$V^{c} \left( G \right) = \frac{{I_{1} }}{2}G^{2} + I_{2} G + I_{3}$$

(A.56)

Similar to the proof of Proposition 1, we can obtain

$$I_{1} = X_{1} ,I_{2} = X_{2} ,I_{3} = X_{3}$$

$$N_{1} = \frac{{ - A_{5} - \Delta_{4} }}{{4\beta \theta^{2} A_{3} }}$$

(A.57)

$$N_{2} = \frac{{\left( {\alpha - A_{0} } \right)\left( {8\beta^{2} \theta \eta k^{2} - A_{0} \left( {A_{5} + \Delta_{4} } \right)} \right)}}{{2\beta \theta \left( {\rho A_{1}^{2} + \Delta_{4} } \right)}}$$

(A.58)

$$N_{3} \left( F \right) = \frac{{\theta A_{3} \left( {\alpha - A_{0} } \right)\left( {8\beta^{2} \theta \eta k^{2} - A_{0} A_{5} - \Delta_{4} + 2{\uprho }A_{0} A_{1}^{2} } \right)}}{{2\rho A_{1}^{2} \left( {\rho A_{1}^{2} + \Delta_{4} } \right)}}N_{2} + \frac{{\beta k^{2} \left( {\alpha - A_{0} } \right)^{2} }}{{A_{1}^{2} }} - \frac{F}{\rho }$$

(A.59)

In particular, the equilibrium solutions with a two-part tariff are the same to the equilibrium solutions in the integrated setting, ${ }\tau^{C} = \tau^{I}$,${ }G^{C} = G^{I}$,${ }p^{C} = p^{I}$.

Functions (24) and (25) represent the two members’ profits, that is, $J_{{\text{m}}}^{C}$ and $J_{{\text{r}}}^{C}$, where

$$M_{1} = I_{1} - N_{1}$$

(A.60)

$$M_{2} = I_{2} - N_{2}$$

(A.61)

$$M_{3} = I_{3} - N_{3} \left( F \right)$$

(A.62)

Proof of Corollary 5

Based on Constraint (26), we can obtain

$$\frac{{M_{1} }}{2}G^{2} + M_{2} G + M_{3} \left( F \right) - \frac{{Y_{1} }}{2}G^{2} - Y_{2} G - Y_{3} > 0$$

(A.63)

i.e.,

$$\frac{F}{\rho } > J_{m}^{D} - J_{m}^{C} \left( 0 \right)$$

(A.64)

Thus, $F$ satisfies the situation, which is $F > {\uprho }\left( {J_{m}^{D} - J_{m}^{C} \left( 0 \right)} \right)$.

Based on Constraint (27), we can obtain

$$\frac{{Z_{1} }}{2}G^{2} + Z_{2} G + Y_{3} - \frac{{N_{1} }}{2}G^{2} - N_{2} G - N_{3} \left( F \right) > 0$$

(A.65)

namely,

$$\frac{F}{\rho } < J_{r}^{C} \left( 0 \right) - J_{r}^{D}$$

(A.66)

Thus, $F$ satisfies the situation, which is $F < {\uprho }\left( {J_{r}^{C} \left( 0 \right) - J_{r}^{D} } \right)$.

We can obtain

$$\begin{aligned} F_{2} - F_{1} = & \rho \left( {J_{r}^{C} \left( 0 \right) - J_{r}^{D} } \right) - \rho \left( {J_{m}^{D} - J_{m}^{C} \left( 0 \right)} \right) = \rho J_{r}^{C} \left( 0 \right) - \rho J_{r}^{D} - \rho J_{m}^{D} + \rho J_{m}^{C} \left( 0 \right) \\ = & \left( {\rho J_{r}^{C} \left( 0 \right) + \rho J_{m}^{C} \left( 0 \right)} \right) - \left( {\rho J_{r}^{D} + \rho J_{m}^{D} } \right) = \rho \left( {J^{I} - J^{D} } \right) > 0 \\ \end{aligned}$$

(A.67)

Thus, $F$ should satisfy $\rho \left( {J_{m}^{D} - J_{m}^{C} \left( 0 \right)} \right) < F < \rho \left( {J_{r}^{C} \left( 0 \right) - J_{r}^{D} } \right)$.

Appendix B

Key variable substitutions and steady-state strategies in this study are as follows:

$A_{0} \equiv E_{0} \left( {\beta s + \gamma } \right)$, $A_{1} \equiv 2\beta k - A_{0}^{2}$,${ }A_{2} \equiv 2\eta \theta A_{0} - \left( {\rho + 2\delta } \right)A_{1}$, $A_{3} \equiv 4\beta k - A_{0}^{2}$, $A_{4} \equiv 2\eta \theta A_{0} - \left( {\rho + 2\delta } \right)A_{3}$, $A_{5} \equiv 2\eta \theta A_{0} A_{3} - \left( {\rho + 2\delta } \right)A_{1}^{2}$,

$\Delta_{1} \equiv \sqrt {A_{2}^{2} - 8\beta k\theta^{2} \eta^{2} }$, $\Delta_{2} \equiv \sqrt {A_{4}^{2} - 16\beta k\theta^{2} \eta^{2} }$, ${\Delta }_{3} \equiv \sqrt {\rho^{2} A_{3}^{4} - 8\beta A_{3} \left( {\rho A_{3} - \Delta_{2} } \right)B_{1}^{2} }$, ${\Delta }_{4} \equiv \sqrt {A_{5}^{2} - 16\beta^{2} \theta^{2} \eta^{2} kA_{3} }$,

$B_{1} \equiv { }k\eta + \theta A_{0} Y_{1}$, $B_{2} \equiv k\alpha - kA_{0} + \theta A_{0} Y_{2}$, $B_{3} \equiv 4\beta \theta Y_{2} + \alpha A_{0} - A_{0}^{2}$,

$X_{1} = \frac{{ - A_{2} - \Delta_{1} }}{{4\beta \theta^{2} }}$,${ }X_{2} = \frac{{\left( {\alpha - A_{0} } \right)\left( {2\eta \theta A_{1} + \left( {\rho + 2\delta } \right)A_{0} A_{1} - \Delta_{1} A_{0} } \right)}}{{2\beta \theta \left( {\rho A_{1} + \Delta_{1} } \right)}}$,

$Y_{1} = \frac{{ - A_{4} - \Delta_{2} }}{{8\beta \theta^{2} }}$, $Y_{2} = \frac{{\left( {\alpha - A_{0} } \right)\left( {2\eta \theta A_{3} + \left( {\rho + 2\delta } \right)A_{0} A_{3} - A_{0} \Delta_{2} } \right)}}{{4\beta \theta \left( {\rho A_{3} + \Delta_{2} } \right)}}$,

$R_{1} = \frac{{\Delta_{1} - \rho A_{1} }}{{2A_{1} }} > 0$,$R_{2} = \frac{{\Delta_{2} - \rho A_{3} }}{{2A_{3} }} > 0$,

$G_{\infty }^{I} = \frac{{4\theta \left( {\alpha - A_{0} } \right)A_{1} \left( {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right)}}{{\left( {\Delta_{1} + \rho A_{1} } \right)\left( {\Delta_{1} - \rho A_{1} } \right)}}$, $\tau_{\infty }^{I} = \frac{\delta }{\theta }G_{\infty }^{I}$, $p_{\infty }^{I} = \frac{{k\alpha + kE_{0} \left( {\beta s - \gamma } \right) - \alpha sE_{0} A_{0} - \theta E_{0} \left( {\beta s - \gamma } \right)X_{2} + \left( {\eta k - \eta sE_{0} A_{0} - \theta E_{0} \left( {\beta s - \gamma } \right)X_{1} } \right)G_{\infty }^{I} }}{{A_{1} }}$,

$G_{\infty }^{D} = \frac{{4\theta \left( {\alpha - A_{0} } \right)A_{3} \left( {\eta \theta + \left( {\rho + \delta } \right)A_{0} } \right)}}{{\left( {\Delta_{2} + \rho A_{3} } \right)\left( {\Delta_{2} - \rho A_{3} } \right)}}$, $\tau_{\infty }^{D} = \frac{\delta }{\theta }G_{\infty }^{D}$, $p_{\infty }^{D} = \frac{{kE_{0} \left( {\beta s - 3\gamma } \right) + 3k\alpha - \alpha sE_{0} A_{0} - \theta E_{0} \left( {\beta s - 3\gamma } \right)Y_{2} + \left( {3\eta k - \eta sE_{0} A_{0} - \theta E_{0} \left( {\beta s - 3\gamma } \right)Y_{1} } \right)G_{\infty }^{D} }}{{A_{3} }}$,$w_{\infty }^{D} = \frac{{2k\alpha + 2kE_{0} \left( {\beta s - \gamma } \right) - \alpha sE_{0} A_{0} - 2\theta E_{0} \left( {\beta s - \gamma } \right)Y_{2} + \left( {2\eta k - \eta sE_{0} A_{0} - 2\theta E_{0} \left( {\beta s - \gamma } \right)Y_{1} } \right)G_{\infty }^{D} }}{{A_{3} }}.$