Aggregation techniques for frequency assignment in public transportation

Abstract

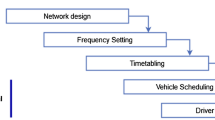
In public transportation, frequency assignment is a sub-problem of line planning which is responsible for assigning each route of a line a certain frequency with which they are serviced by vehicles. Frequency assignment is among the most important decision problems for optimizing the waiting times in a transportation network and is often a very complex matter. This paper focuses on different aggregation techniques for reducing the computational effort to obtain (near-)optimal line frequencies. In detail, the influence of different model formulations and strategies for customer input data aggregation are investigated. For this purpose, six models are provided, their computational complexity is investigated and suitable mixed-integer mathematical programs are developed. These models vary in the levels of line utilization detail and predict the resulting travel times. Both aggregation techniques are evaluated according to their influence on the solution quality, which is determined by the transport suppliers’ point of view as forecast accuracy of the weighted number of customers using the transport. This comprehensive computational study reveals that some model formulations reduce the computational effort considerably by only small losses in line frequency quality. Furthermore, dramatically compressed customer data lead to (near-)optimal line frequencies.

Appendix A: Computational complexity of FAP

In this section first NP-hardness of FAP is proofed by transforming instances from Multicut on stars, which is well known to be strongly NP-complete (Elbassioni et al. 2009; Garg et al. 1997). Then, it will be shown that this proof is applicable to all other variants of FAP.

Multicut on stars (Elbassioni et al. 2009; Hu 1969): Given an undirected star $G = (V,E,c)$, i.e., a tree with depth one, with edge-weights equal to 1, a set $C \subseteq V \times V$ of source-terminal pairs and a positive integer $K$, does there exist a multicut, i.e., an edge-set $E^{\prime} \subseteq E$ such that the removal of $E^{\prime}$ from $E$ disconnects all source-terminal pairs, with $\left| {E^{\prime}} \right| \le K$?

In the course of the presented proofs this special case is referenced, if naming the Multicut problem. In addition, we presuppose w.l.o.g. that the transportation network of FAP is undirected, since each line operates in both directions and additional links may be removed.

For each instance of Multicut, an instance of FAP with transportation network $G$ and a line plan budget of $D = \left| E \right|\,\, \cdot \,\,(K + 1)$ is generated. Further it is assumed that each edge is operated by a single line which has a riding time of only 1 time unit. There also exist only two possible frequencies for these lines, i.e., a high frequency with inter-arrival time $t_{1}^{i} = 2$ and costs $d_{l1} = \left| E \right| + 1$ and a low frequency with $t_{2}^{i} = 2 \cdot (\left| E \right| + 1)$ and $d_{l2} = 1$. For each source-terminal pair $(\upsilon_{1} ,\,\upsilon_{2} ) \in C$ we introduce a customer who intends to travel on the path from $\upsilon_{1}$ to $\upsilon_{2}$ and generates a benefit of 1 for the transport supplier. Each customer from a node-pair in $C \cap E$ is willing to accept a travel time of 2 time units and each customer from a node-pair in $C\backslash E$ is willing to accept a travel time of $\left| E \right| + 4$ time units. If we claim a revenue of $\left| C \right|$ for the transport supplier, finding a feasible multicut is equivalent to solving the corresponding FAP instance.

Given a feasible solution of an arbitrary multicut instance, a feasible solution for the corresponding FAP instance can be determined in polynomial time by setting the inter-arrival times of lines operating on multicut-edges $e \in E^{\prime}$ to 2 and of all other lines to $2 \cdot (\left| E \right| + 1)$. Then, the costs of the line plan do not exceed $K\,\, \cdot \,\,(\left| E \right|\,\, + \,\,1)\,\, + \,\,(\left| E \right|\,\, - \,\,K)\,\, \cdot \,\,1\, = \,\,\left| E \right|\,\,\, \cdot \,\,\,(K + 1)\,\, = \,\,D$ and all customers are willing to use the transport, since the expected travel time of a trip on a single edge is at most 2 time units, i.e., 1 time unit waiting time and 1 time unit riding time, and on two edges at most $\left| E \right| + 4$ time units, i.e., $\left| E \right| + 2$ time units for waiting and 2 time units for riding. Thus, this line plan leads to a total benefit of $\left| C \right|$.

On the other hand, each feasible solution of FAP is also a Yes-instance of Multicut, since the budget is so tight that the high frequency is assigned to at most $K$ lines and each customer using the transport has to ride with at least one of these lines. Otherwise, the expected waiting times would be higher than the accepted travel times of 2 and $\left| E \right| + 4$, respectively, and some customers would not use the transport.

In the generated FAP-instances, there exists only one path between each pair of nodes $\upsilon_{1} ,\,\upsilon_{2} \in V$ and for each customer only one possible route in the transportation network. Thus, the aforementioned complexity proof holds for all three cases of customer routes, i.e., deterministic customer paths, arbitrary customer paths and arbitrary customer graphs. Furthermore, there exists only one line on each edge, so that there exists exactly one possible connection for each customer. Thus, the complexity proof for FAP is independent from the considered type of customer connection, i.e., the proof is applicable to deterministic connections, single connections, and connection strategies. Only for the frequency assignment problems applying connection strategies, this proof has to be slightly altered, since the expected waiting times are calculated in another way. In this case, the feasible inter-arrival times of 2 and $2 \cdot (\left| E \right| + 1)$ must be replaced by inter-arrival times of $\frac{1}{\alpha }$ and $\frac{\left| E \right| + 1}{\alpha }$, respectively. The associated cost factors do not have to be changed. Then, the aforementioned complexity proof applies to all problem variants of FAP.