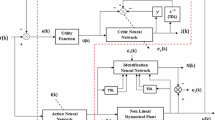
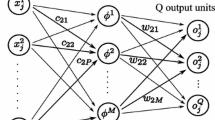
Abstract
An important problem in the learning process when training feedforward artificial neural networks is the occurrence of temporary minima which considerably slows down learning convergence. In a series of previous works, we analyzed this problem by deriving a dynamical system model which is valid in the vicinity of temporary minima caused by redundancy of nodes in the hidden layer. We also demonstrated how to incorporate the characteristics of the dynamical model into a constrained optimization algorithm that allows prompt abandonment of temporary minima and acceleration of learning. In this work, we revisit the constrained optimization framework in order to develop a closed-form solution for the evolution of critical dynamical system model parameters during learning in the vicinity of temporary minima. We show that this formalism is equivalent to matrix perturbation theory which was discussed in a previous work, but that the closed-form solution presented in the present paper allows for a weight update rule which is linear to the number of the network’s weights. In terms of computational complexity, this is equivalent to that of the simple back-propagation weight update rule. Simulations demonstrate the computational efficiency and effectiveness of this approach in reducing the time spent in the vicinity of temporary minima as suggested by the analysis.








Similar content being viewed by others
References
Amari S. Differential-geometrical method in statistics. Berlin: Springer; 1985.
Amari S. Natural gradient works efficiently in learning. Neural Comput. 1998;10:251–76.
Amari S, Park H, Fukumizu K. Adaptive method of realizing natural gradient learning for multilayer perceptrons. Neural Comput. 1999;12:1399–409.
Amari S, Nagaoka H. Methods of information geometry. Providence, RI: American Mathematical Society; 2000.
Ampazis N, Perantonis S, Taylor J. Acceleration of learning in feedforward networks using dynamical systems analysis and matrix perturbation theory. In: International joint conference on neural networks. vol. 3. 1999. p. 1850–1855.
Ampazis N, Perantonis S, Taylor J. Dynamics of multilayer networks in the vicinity of temporary minima. Neural Netw. 1999;12:43–58.
Ampazis N, Perantonis SJ, Taylor JG. A dynamical model for the analysis and acceleration of learning in feedforward networks. Neural Netw. 2001;14:1075–88.
Beer RD. Dynamical approaches to cognitive science. Trends Cogn Sci. 2000;4:91–9.
Bishop CM. Neural networks for pattern recognition. Oxford: Oxford University Press; 1996.
Botvinick M. Commentary: why i am not a dynamicist. Top Cogn Sci. 2012;4:78–83.
Boyce WE, DiPrima RC. Elementary differential equations and boundary value problems. London: Wiley; 1986.
Coddington EA, Levinson N. Theory of ordinary differential equations. New York: McGraw-Hill; 1955.
Fahlman SE. Faster learning variations on back propagation: an empirical study. In: Proceedings of the 1988 connectionist models summer school. 1988. p. 38–51.
Fusella PV. Dynamic systems theory in cognitive science: major elements, applications, and debates surrounding a revolutionary meta-theory. Dyn Psychol. 2012–13. http://wp.dynapsyc.org/
Gelder TV. The dynamical hypothesis in cognitive science. Behav Brain Sci. 1997;21:615–65.
Guo H, Gelfand SB. Analysis of gradient descent learning algorithms for multilayer feedforward networks. IEEE Trans Circuits Syst. 1991;38:883–94.
Gros C. Cognitive computation with autonomously active neural networks: an emerging field. Cogn Comput. 2009;1(1):77–90.
Heskes T. On “Natural” learning and pruning in multilayered perceptrons. Neural Comput. 2000;12:881–901.
Jacobs RA. Increased rates of convergence through learning rate adaptation. Neural Netw. 1988;1:295–307.
Liang P. Design artificial neural networks based on the principle of divide-and-conquer. In: Proceedings of international conference on circuits and systems. 1991. p. 1319–1322.
Murray AF. Analog VLSI and multi-layer perceptrons—accuracy, noise, and on-chip learning. In: Proceedings of second international conference on microelectronics for neural networks. 1991. p. 27–34.
Parker D. Learning logic: casting the cortex of the human brain in silicon. Technical report TR-47 Invention Report 581–64, Center for Computational Research in Economics and Management Science, MIT. 1985.
Perantonis SJ, Karras DA. An efficient constrained learning algorithm with momentum acceleration. Neural Netw. 1995;8:237–9.
Riedmiller M, Braun H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In: Proceedings of the international joint conference on neural networks. 1993;1:586–91.
Roth I, Margaliot M. Analysis of artificial neural network learning near temporary minima: a fuzzy logic approach. Fuzzy Sets Syst. 2010;161:2569–84.
Shapiro LA. Dynamics and cognition. Minds Mach. 2013;23:353–75.
Schöner G. Dynamical systems approaches to cognition. In: Cambridge handbook of computational cognitive modeling. Cambridge: Cambridge University Press; 2007.
Seth A. Explanatory correlates of consciousness: theoretical and computational challenges. Cogn Comput. 2009;1(1):50–63.
Spivey MJ. The continuity of mind. Oxford: Oxford University Press; 2007.
Sussmann HJ. Uniqueness of the weights for minimal feedforward nets with a given input–output map. Neural Netw. 1992;5:589–93.
Trefethen LN, Bau D. Numerical linear algebra. USA: Society for Industrial and Applied Mathematics; 1997.
Tyukin I, van Leeuwen C, Prokhorov D. Parameter estimation of sigmoid superpositions: dynamical system approach. Neural Comput. 2003;15:2419–55.
Woods D. Back and counter propagation abbreviations. In: Proceedings of the IEEE international conference on neural networks. 1988.
Yang HH, Amari S. Complexity issues in natural gradient descent method for training multilayer perceptrons. Neural Comput. 1998;10:2137–57.
Zweiri YH. Optimization of a three-term backpropagation algorithm used for neural network learning. Int J Comput Intell. 2006;3(4):322–7.
Acknowledgments
Nicholas Ampazis would like to express his gratitude to his supervisor late Professor John G. Taylor for the guidance, patience, and continuous encouragement. John has been a source of inspiration to everyone that had the privilege to meet him and has left a shining imprint on the scientific community.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Let
with
and
If we let
and
then, we can write
Let
A simple calculation shows that
where
We want to calculate
Recall that
Using simple properties of the derivatives and (44), we get that
which, using again simple properties of the derivatives, gives
which implies that
On the other hand, we obviously have that
Using (45) and (46) and simple properties of the derivatives, we get that
Let
Combining (47), (48), and (49), we get that
For the evaluation of \(\frac{\partial }{\partial {\varvec{\omega }}}({{\varvec{u}}}^T{{\varvec{J}}}{{\varvec{u}}})\) , we have:
Using simple properties of the derivatives and (44), we get that
which, using again simple properties of the derivatives and (44), gives
which implies that
Using simple properties of the derivatives and (51), we get that
Using simple properties of the derivatives and (52) and (53), we get that
On the other hand, using simple properties of the derivatives and (51), we get that
Using (54) and (55) and simple properties of the derivatives, we get that
Combining (48), (49) and (56), we get that
For a Jacobian matrix of size \(Q \times Q\), it follows that there are Q derivatives to evaluate. By simply taking the expression for the differential of Eq. (27) and evaluating it at small perturbations by finite differences, we would have to evaluate Q such terms (one for each component of the state vector \({{\varvec{\varOmega }}}\)), each requiring O(Q) operations. Thus, the total computational effort required to evaluate all the derivatives scales as \(O(Q^2)\).
Equations (50) and (57) allow the derivatives to be propagated back and evaluated in O(Q) operations similarly to the back-propagation algorithm which requires O(W) operations, where W is the number of the network’s weights [9]. This follows from the fact that both the forward phase [evaluation of Eq. (43)] and the backward propagation phases are O(Q), and the evaluation of the derivatives require O(Q) operations. Thus the closed-form solution has reduced the computational complexity from \(O(Q^2)\) of the finite differences method to O(Q) for each input vector, which results in a significant computational gain.
Rights and permissions
About this article
Cite this article
Ampazis, N., Perantonis, S.J. & Drivaliaris, D. Improved Jacobian Eigen-Analysis Scheme for Accelerating Learning in Feedforward Neural Networks. Cogn Comput 7, 86–102 (2015). https://doi.org/10.1007/s12559-014-9263-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12559-014-9263-2