Abstract
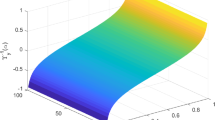
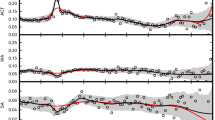
The age-dependent population equation with migration source is a partial differential equation describing the variation of population density in a given area over time. In the traditional age-dependent population equation with migration source, the strength of the migration source is deterministic. In practice, however, the migration source is often affected by noise caused by environmental, policy and other factors. To capture this noise, some scholars have applied the Wiener process. However, the prediction accuracy of the noise model based on the Wiener process may be low. This paper proposes the adoption of the Liu process in uncertainty theory as an alternative tool for modelling noise, which improves the prediction accuracy of the model. The paper then deduces the uncertain age-dependent population equation with migration source based on the Liu process. Furthermore, the analytic solution to the equation and its inverse uncertainty distribution are derived. Additionally, the parameters of the uncertain age-dependent population equation with migration source are estimated, and numerical examples are analysed to validate the model. This paper makes the following contributions: (1) describing the continuous migration source using a Liu process; (2) establishing a new type of uncertain differential equation depicting the variation in population density caused by migration noise in practice; (3) extending the applicability of uncertainty theory to demographic theory.






Similar content being viewed by others
Notes
MATLAB R2020a, 9.8.0.1323502, maci64, Symbolic Math Toolbox,sym and solve functions.
References
Anita S (2000) Analysis and control of age-dependent population dynamics. Kluwer, Netherlands
Arenas A, Gonzalez-Parra G, Espriella N (2021) Nonlinear dynamics of a new seasonal epidemiological model with age-structure and nonlinear incidence rate. Comput Appl Math 40(2):1–27
Bouchaib K, Abdelfatah K (2021) Fractional optimal control problem for an age-structured model of COVID-19 transmission. Chaos Solitons Fractals 143(6):110–129
Chen X, Liu B (2010) Existence and uniqueness theorem for uncertain differential equations. Fuzzy Opt Decision Making 9(1):69–81
Dawidowicz AL, Poskrobko A (2018) Stability problem for the age-dependent predator-prey model. Evol Equ Control Theory 7(1):79–93
Duan D, Niu B, Wei J (2019) Local and global hopf bifurcation in a neutral population model with age structure. Math Methods Appl Sci 42(14):4747–4764
Gao R, Ralescu DA (2019) Uncertain wave equation for vibrating string. IEEE Trans Fuzzy Syst 27(7):1323–1331
Gao Y, Jia L (2022) Stability in distribution for uncertain delay differential equations based on new lipschitz condition. J Ambient Intell Human Comput. https://doi.org/10.1007/s12652-022-03826-9
Gholi Z, Heidari-Beni M, Feizi A et al (2016) The characteristics of pre-diabetic patients associated with body composition and cardiovascular disease risk factors in the iranian population. J Res Med Sci. https://doi.org/10.4103/1735-1995.179888
Kaygermazov A, Shakov K, Kudaeva F (2021) Mckendrick-tornquist age-dependent population model. J Math Sci 253(5):511–519
Lee I, Sang Y, Won D (2021) A data-driven forecast netting approach for reliable demand forecasting. J Data Inform Manag 3(2):141–154
Li R, Pang W, Wang Q (2007) Numerical analysis for stochastic age-dependent population equations with poisson jumps. J Math Anal Appl 327(2):1214–1224
Lio W, Liu B (2021) Initial value estimation of uncertain differential equations and zero-day of COVID-19 spread in China. Fuzzy Opt Decision Making 20(3):177–188
Liu B (2008) Fuzzy process, hybrid process and uncertain process. J Uncertain Syst 2(1):3–16
Liu B (2009) Some research problems in uncertainy theory. J Uncertain Syst 3(1):3–10
Liu B (2015) Uncertainty Theory. Springer-Verlag, Berlin
Liu Z, Jia L (2020) Moment estimations for parameters in uncertain delay differential equations. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology 39(1):841–849
Lv Y, Pei Y, Yuan R (2021) On a periodic age-structured mosquito population model with spatial structure. Nonlinear Analysis Real World Applications 61(16):315–337
Movassagh A, Alzubi J, Gheisari M (2022) Artificial neural networks training algorithm integrating invasive weed optimization with differential evolutionary model. J Ambient Intell Human Comput. https://doi.org/10.1007/s12652-020-02623-6
Nafchi RF, Vanani HR, Pashaee KN et al (2022) Investigation on the effect of inclined crest step pool on scouring protection in erodible river beds. Nat Hazards. https://doi.org/10.1007/s11069-021-04999-w
Ostad A, Mohammad S, Saeid E et al (2018) Comparison of solutions of saint-venant equations by characteristics and finite difference methods for unsteady flow analysis in open channel. Int J Hydrol Sci Technol 8(3):229–243
Pollard J (1966) On the use of the direct matrix product in analysing certain stochastic population models. Biometrika 53(3):397–415
Qiang L, Wang BG, Zhao XQ (2022) A stage-structured population model with time-dependent delay in an almost periodic environment. J Dyn Differ Equ 34(2):341–364
Sheng Y, Gao R, Zhang Z (2017) Uncertain population model with age-structure. J Intell Fuzzy Syst 33(2):1–6
Yang X (2018) Solving uncertain heat equation via numerical method. Appl Math Comput 329:92–104
Yang X, Ni Y (2017) Existence and uniqueness theorem for uncertain heat equation. J Ambient Intell Human Comput 8:717–725
Yang X, Yao K (2017) Uncertain partial differential equation with application to heat conduction. Fuzzy Opt Decision Making 16(3):379–403
Yang X, Liu Y, Park GK (2020) Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fractals 139:110–126
Yao K, Chen X (2013) A numerical method for solving uncertain differential equations. J Intell Fuzzy Syst 25(3):825–832
Yao K, Liu B (2020) Parameter estimation in uncertain differential equations. Fuzzy Opt Decision Making 19(1):1–12
Ye T (2020) Parameter estimation in uncertain heat equations. Preprint at https://doi.org/10.22541/au.160578917.70969813/v1
Zhang Q, Li X (2012) Existence and uniqueness for stochastic age-dependent population with fractional brownian motion. Math Prob Eng 10:3–22
Zhang Q, Liu W, Nie Z (2004) Existence, uniqueness and exponential stability for stochastic age-dependent population. Appl Math Comput 154(1):183–201
Zhang Z, Yang X (2020) Uncertain population model. Soft Comput 24(6):2417–2423
Acknowledgements
This work was supported by grants from the Key Program of the National Statistical Science Research (No.2021LZ28), Natural Science Foundation of Shaanxi Province of China (No.2022JQ-042), the Young Talent Support Program of Xi’an University of Finance and Economics, and the Yanta Scholars Fund of Xi’an University of Finance and Economics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yang, L. Uncertain age-dependent population equation with migration source. J Ambient Intell Human Comput 14, 7411–7425 (2023). https://doi.org/10.1007/s12652-022-04448-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12652-022-04448-x