Self-paced latent embedding space learning for multi-view clustering

Abstract

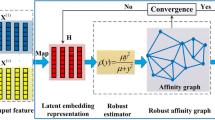
Multi-view clustering (MVC) can integrate the complementary information between different views to remarkably improve clustering performance. However, the existing methods suffer from the following drawbacks: (1) multi-view data are often lying on high-dimensional space and inevitably corrupted by noise and even outliers, which poses challenges for fully exploiting the intrinsic structure of views; (2) the non-convex objective functions prone to becoming stuck into bad local minima; and (3) the high-order structure information has been largely ignored, resulting in suboptimal solution. To alleviate these problems, this paper proposes a novel method, namely Self-paced Latent Embedding Space Learning (SLESL). Specifically, the views are projected into a latent embedding space to dimensional-reduce and clean the data, from simplicity to complexity in a self-paced manner. Meanwhile, multiple candidate graphs are learned in the latent space by using embedded self-expressiveness learning. After that, these graphs are stacked into a tensor to exploit the high-order structure information of views, such that a refined consensus affinity graph can be obtained for spectral clustering. The experimental results demonstrate the effectiveness of our proposed method.

Appendix

1.1 Proof of Lemma 1

Proof

For convenience, we denote the objective of (18) as

$$\begin{aligned} F({\mathbf {p}})=f({\mathbf {p}})+\psi ({\mathbf {p}}) \end{aligned}$$

(33)

where $f({\mathbf {p}})=\left( {\mathbf {p}}^{\intercal } {\mathbf {S}}^{2} {\mathbf {p}}\right) ^{1 / 2}$ and $\psi ({\mathbf {p}})=\tau / 2\Vert {\mathbf {p}}-{\mathbf {h}}\Vert ^{2}$.

Note that $F({\mathbf {p}})$ is convex, and an optimum of (18) corresponds to a stationary point of $F({\mathbf {p}})$. Therefore, to find the optimal solution of the problem in (18), we first derive the subgradient of $F({\mathbf {p}})$, and then seek its stationary point [36].

Since $F({\mathbf {p}})$ can be expressed as the sum of $f({\mathbf {p}})$ and $\psi ({\mathbf {p}})$, let us derive the subgradients of $f({\mathbf {p}})$ and $\psi ({\mathbf {p}})$, respectively. The subgradient of $\psi ({\mathbf {p}})$ with respect to ${\mathbf {p}}$ is as follows:

$$\begin{aligned} \partial \psi ({\mathbf {p}})=\tau ({\mathbf {p}}-{\mathbf {h}}) \end{aligned}$$

(34)

For $f({\mathbf {p}})$, note that it can be rewritten as $f({\mathbf {p}})=\Vert \mathbf {S p}\Vert$. Based on [45], the subgradient of $f({\mathbf {p}})$ with respect to ${\mathbf {p}}$ is as follows:

$$\begin{aligned} \partial f({\mathbf {p}})= {\left\{ \begin{array}{ll}\left\{ {\mathbf {S}}^{\intercal } {\mathbf {r}} \mid \Vert {\mathbf {r}}\Vert \le 1\right\} , &{} \text{ if } \mathbf {S p}={\mathbf {0}}_{q} \\ \frac{{\mathbf {S}}^{2} {\mathbf {p}}}{\Vert {\mathbf {S}}\Vert }, &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

(35)

Recall that the diagonal matrix ${\mathbf {S}}$, in which all the diagonal elements are positive, is a positive definite matrix. As a result, $\mathbf {S p}={\mathbf {0}}_{q}$ is equivalent to ${\mathbf {p}}={\mathbf {0}}_{q}$.

In summary, the subgradient of $F({\mathbf {p}})$ can be expressed as

$$\begin{aligned} \partial F({\mathbf {p}})= {\left\{ \begin{array}{ll}\left\{ {\mathbf {S}}^{\intercal } {\mathbf {r}}+\tau ({\mathbf {p}}-{\mathbf {h}}) \mid \Vert {\mathbf {r}}\Vert \le 1\right\} , &{} \text{ if } {\mathbf {p}}={\mathbf {0}}_{q} \\ \frac{{\mathbf {S}}^{2} {\mathbf {p}}}{\Vert \mathbf {S p}\Vert }+\tau ({\mathbf {p}}-{\mathbf {h}}), &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

(36)

Based on the above two cases, let us discuss the stationary point of $F({\mathbf {p}})$ accordingly in two cases as follows.

• 1. When ${\mathbf {p}}={\mathbf {0}}_{q}$, we have

  $$\begin{aligned} \partial F({\mathbf {p}})=\left\{ {\mathbf {S}}^{\intercal } {\mathbf {r}}+\tau ({\mathbf {p}}-{\mathbf {h}}) \mid \Vert {\mathbf {r}}\Vert \le 1\right\} \end{aligned}$$

  (37)

  Note that ${\mathbf {p}}^{*}={\mathbf {0}}_{q}$ is a stationary point, if and only if

  $$\begin{aligned} {\mathbf {0}}_{q} \in \left\{ {\mathbf {S}}^{\intercal } {\mathbf {r}}+\tau \left( {\mathbf {p}}^{*}-{\mathbf {h}}\right) \mid \Vert {\mathbf {r}}\Vert \le 1\right\} \end{aligned}$$

  (38)

  In other words, ${\mathbf {p}}^{*}={\mathbf {0}}_{q}$ is a stationary point, if and only if there is a vector ${\mathbf {r}}$ that satisfies the following two conditions:

  $$\begin{aligned} \begin{aligned}&{\mathbf {S}}^{\intercal } {\mathbf {r}}+\tau \left( {\mathbf {p}}^{*}-{\mathbf {h}}\right) ={\mathbf {0}}_{q} \\&\Vert {\mathbf {r}}\Vert \le 1 \end{aligned} \end{aligned}$$

  (39)

  Recalling that ${\mathbf {p}}^{*}={\mathbf {0}}_{q}$ and ${\mathbf {S}}$ is positive definite, (39) is equivalent to ${\mathbf {r}}=\tau {\mathbf {S}}^{-1} {\mathbf {h}}$. Combining this with inequality (39), we arrive at

  $$\begin{aligned} \left\| {\mathbf {S}}^{-1} {\mathbf {h}}\right\| \le \frac{1}{\tau } \end{aligned}$$

  (40)

  Therefore, ${\mathbf {p}}^{*}={\mathbf {0}}_{q}$ is a stationary point of $F({\mathbf {p}})$, if and only if $\left\| {\mathbf {S}}^{-1} {\mathbf {h}}\right\| \le (1 / \tau )$. In particular, when $\left\| {\mathbf {S}}^{-1} {\mathbf {h}}\right\| \le (1 / \tau )$, we have ${\mathbf {r}}=\tau {\mathbf {S}}^{-1} {\mathbf {h}}$ that satisfies (38).

• 2. When ${\mathbf {p}} \ne {\mathbf {0}}_{q}$, we have

  $$\begin{aligned} \partial F({\mathbf {p}})=\frac{{\mathbf {S}}^{2} {\mathbf {p}}}{\Vert \mathbf {S p}\Vert }+\tau ({\mathbf {p}}-{\mathbf {h}}) \end{aligned}$$

  (41)

  As a result, ${\mathbf {p}}^{*} \ne {\mathbf {0}}_{q}$ is a stationary point, if and only if ${\mathbf {S}}^{2} {\mathbf {p}}^{*} /\left\| \mathbf {S p}^{*}\right\| +\tau \left( {\mathbf {p}}^{*}-{\mathbf {h}}\right) ={\mathbf {0}}_{q}$. This condition can be rewritten as

  $$\begin{aligned} \left( \frac{{\mathbf {S}}^{2}}{\left\| {\mathbf {S}} {\mathbf {p}}^{*}\right\| }+\tau {\mathbf {I}}\right) {\mathbf {p}}^{*}=\tau {\mathbf {h}} \end{aligned}$$

  (42)

  By defining a scalar $\alpha \triangleq \left\| \mathbf {S p}^{*}\right\|$, we rewrite ${\mathbf {p}}^{*}$ as

  $$\begin{aligned} {\mathbf {p}}^{*}=\left( \frac{{\mathbf {S}}^{2}}{\tau \alpha }+{\mathbf {I}}\right) ^{-1} {\mathbf {h}} \end{aligned}$$

  (43)

  Since ${\mathbf {p}}^{*} \ne {\mathbf {0}}_{q}$, we have $\mathbf {S p}^{*} \ne {\mathbf {0}}_{q}$. Accordingly, we have $\alpha =\left\| \mathbf {S p}^{*}\right\| >0$. Moreover, given $\alpha =\left\| \mathbf {S p}^{*}\right\|$ and $\alpha >0$, we conclude that $\alpha$ is the positive root of

  $$\begin{aligned} \alpha ^{2}=\left( {\mathbf {p}}^{*}\right) ^{\intercal } {\mathbf {S}}^{2} {\mathbf {p}}^{*} \end{aligned}$$

  (44)

  By substituting (43) into (44), we obtain

  $$\begin{aligned} \alpha ^{2}=\tau ^{2} \alpha ^{2} {\mathbf {h}}^{\intercal } {\text {diag}}\left( \left\{ \frac{s_{i}^{2}}{\left( s_{i}^{2}+\tau \alpha \right) ^{2}}\right\} _{1 \le i \le q}\right) {\mathbf {h}} \end{aligned}$$

  (45)

  Dividing both the sides of (45) by $\tau ^{2} \alpha ^{2}$, we arrive at (20).

Now, if the positive root of the equation in (20) exists, we can first obtain $\alpha$, and then obtain ${\mathbf {p}}^{*}$ by substituting $\alpha$ into (43). In the following, we show the existence condition of the positive root of (20).

For convenience, we define the following function with respect to $\alpha$:

$$\begin{aligned} \ell (\alpha ) \triangleq {\mathbf {h}}^{\intercal } {\text {diag}}\left( \left\{ \frac{s_{i}^{2}}{\left( \tau \alpha +s_{i}^{2}\right) ^{2}}\right\} _{1 \le i \le q}\right) {\mathbf {h}}-\frac{1}{\tau ^{2}} \end{aligned}$$

(46)

With this definition, (20) can be rewritten as $\ell (\alpha )=0$. We can verify the following properties of $\ell (\alpha )$.

Based on (46) and the intermediate value theorem [46], it is easy to verify that there exists a positive scalar $\alpha$ which satisfies $\ell (\alpha )=0$ if and only if $\Vert {\mathbf {S}}^{-1} {\mathbf {h}}\Vert ^{2}-(1 / \tau ^{2})>0$, namely

$$\begin{aligned} \left\| {\mathbf {S}}^{-1} {\mathbf {h}}\right\| >\frac{1}{\tau } \end{aligned}$$

(47)

In particular, when $\Vert {\mathbf {S}}^{-1} {\mathbf {h}}\Vert >1 / \tau$, the positive root of the equation $\ell (\alpha )=0$ exists, and such positive root is unique due to the strictly decreasing property of $\ell (\alpha )$. Furthermore, let $\alpha ^{*}$ be the unique positive root of $\ell (\alpha )=0$, then we can prove the following inequality that determines the range of $\alpha ^{*}$:

$$\begin{aligned} \max \left( 0, \alpha _{l}\right) \le \alpha ^{*} \le \alpha _{u} \end{aligned}$$

(48)

in which $\alpha _{u}=({\mathbf {h}}^{\intercal } {\text {diag}}(\{s_{i}^{2}\}_{1 \le i \le q}) {\mathbf {h}})^{1 / 2}-s_{q}^{2} / \tau$ is the positive root of an equation $f_{u}(\alpha )=0; \alpha _{l}=({\mathbf {h}}^{\intercal } {\text {diag}}(\{s_{i}^{2}\}_{1 \le i \le q}) {\mathbf {h}})^{1 / 2}-$ $s_{1}^{2} / \tau$ is the larger root of another equation $f_{l}(\alpha )=0$, where the two functions $f_{u}(\alpha )$ and $f_{l}(\alpha )$ are defined as

$$\begin{aligned} \begin{aligned}&f_{u}(\alpha )={\mathbf {h}}^{\intercal } \frac{{\text {diag}}\left( \left\{ s_{i}^{2}\right\} _{1 \le i \le q}\right) }{\left( \tau \alpha +s_{q}^{2}\right) ^{2}} {\mathbf {h}}-\frac{1}{\tau ^{2}} \\&f_{l}(\alpha )={\mathbf {h}}^{\intercal } \frac{{\text {diag}}\left( \left\{ s_{i}^{2}\right\} _{1 \le i \le q}\right) }{\left( \tau \alpha +s_{1}^{2}\right) ^{2}} {\mathbf {h}}-\frac{1}{\tau ^{2}} \end{aligned} \end{aligned}$$

(49)

In particular, $f_{u}(\alpha )$ is obtained by the amplification of $\ell (\alpha )$ by replacing $(\tau \alpha +s_{i}^{2})$ with $(\tau \alpha +s_{q}^{2})$, while $f_{l}(\alpha )$ is obtained by the minification of $\ell (\alpha )$ by replacing $(\tau \alpha +s_{i}^{2})$ with $(\tau \alpha +s_{l}^{2})$.

Therefore, $f_{u}(\alpha )=0$ has a unique positive root, namely $\alpha _{u}$, which is no less than $\alpha ^{*}$. Moreover, $\alpha _{l}$ [i.e., the larger root of $f_{l}(\alpha )=0$ ] is no greater than $\alpha ^{*}$, but not necessarily positive. As a result, the inequalities in (48) are verified. Accordingly, we can obtain $\alpha ^{*}$ by the bisection search method [41] within the searching range $[\max (0, \alpha _{l}), \alpha _{u}]$.

In summary, if and only if $\Vert {\mathbf {S}}^{-1} {\mathbf {h}}\Vert >(1 / \tau )$ is satisfied, there exists ${\mathbf {p}}^{*} \ne {\mathbf {0}}_{q}$, which is optimal to the problem in (20). In particular, when $\Vert {\mathbf {S}}^{-1} {\mathbf {h}}\Vert >(1 / \tau ), {\mathbf {p}}^{*}$ can be calculated as in (43), where $\alpha$ is the unique positive root of the equation in (20) and can be obtained by the bisection search method [41].

This completes the proof of Lemma 1. $\square$