Influence of vaccination strategies and topology on the herd immunity of complex networks

Abstract

It is well known that non-vaccinated individuals may be protected from contacting a disease by vaccinated individuals in a social network through community protection (herd immunity). Such protection greatly depends on the underlying topology of the social network, the strategy used in selecting individuals for vaccination, and the interplay between these. In this paper, we analyse how the interplay between topology and immunization strategies influences the herd immunity of social networks. First, we introduce an area under curve measure which can quantify the levels of herd immunity in a social network. Then, using this measure, we analyse the above mentioned interplay in three ways: (1) by comparing vaccination strategies across topologies, (2) by analysing the influence of selected topological metrics, and (3) by considering the influence of network growth on herd immunity. For qualitative comparison, we consider three classical topologies (scale-free, random, and small-world) and three vaccination strategies (natural, random, and betweenness-based immunization). We show that betweenness-based vaccination is the best strategy of immunization in static networks, regardless of topology, but its prominence over other strategies diminishes in dynamically growing topologies. We find that the network features that lead to ‘small-worldness’ in networks (low diameter and high clustering) discourage herd immunity, regardless of the vaccination strategy, while preferential mixing (high assortativity) encourages it. In terms of growth, we demonstrate that herd immunity of random networks actually increases with growth, if the proportion of survivors to a secondary infection is considered, while the community protection in scale-free and small-world networks decreases with growth. Our work highlights the complex balance between social network structure and vaccination strategies in influencing community protection, and contributes a numerical measure to quantify this.

1 Introduction

The speed and penetration of epidemic spread depends on a number of factors—the transmissibility of the contagion, the mode of transmission, and the structure of the social networks. Therefore, these factors have to be taken into account in designing effective vaccination strategies for a population. It is rarely possible to vaccinate an entire population against a potential epidemic. The vaccinating entity may not have the resources to do so, and the individuals may be indifferent, negligent, or even resistant towards the vaccination process. An important concept, therefore, in epidemiology is that a population may be entirely immunized by strategically vaccinating a portion of it (Anderson and May 1990), and this concept is called the ‘herd immunity’. It is obvious that the feasibility of herd immunity, and the resources needed to achieve it on a given population, depend on the topology of the underlying social network.

In many cases [such as chickenpox and measles (Ferrari et al. 2006), which are commonly found in temperate countries yet endemic to all countries worldwide] the spread of an epidemic may immunize a community against subsequent epidemics of the same disease. This is called natural immunization. Natural immunization is different from typical vaccination programmes because it preferentially targets individuals (nodes) who are highly connected. Clinical vaccination, if resources are limited, on the other hand, would give preference to the health considerations of individuals and not to their social connectivity patterns. In terms of connectivity, it can be considered ‘random’, for it selects individuals regardless of their topological placement. Therefore, the effect on network herd immunity by both strategies is different. If the underlying topology of the social network is known, clinical vaccination strategies guided by this topology can also be introduced. This is particularly relevant if we consider ‘social networks’ from a higher level of abstraction (e.g., a network of townships rather than a network of individuals, where it is easier to establish the network structure).

A further complexity arises because of the fact that social networks are constantly under growth. Often the time difference between natural or clinical vaccination and the spread of the next epidemic is very considerable—several years or decades. Within this time children are born, migrants who are not vaccinated enter the community and new ways of interactions between the existing members begin to take place. All of this can effectively change the levels of herd immunity present in a community to a particular disease.

The goal of this paper is to compare the effect of vaccination strategies on social networks with differing topologies, qualitatively and quantitatively. We model social networks via three well-studied classes of synthesized networks and compare the effect of topology and growth on herd immunity on each of these classes. We are interested in finding whether a particular strategy of vaccination is better suited to a particular class of networks, whether a particular structural metric (such as clustering) encourages or discourages herd immunity, and whether a particular class of networks is more (or less) responsive to growth in terms of herd immunity. In terms of the first question, we build on existing work (Ferrari et al. 2006) yet introduce a new vaccination strategy (vaccination by betweenness order) and compare it to the strategies already studied. Then we further expand on this by studying the influence of structural metrics relevant to each topology, such as clustering coefficient, network diameter, and assortativity. In terms of network growth, we compare the vaccination strategies on each class of networks to see the amount of reduction in herd immunity in each scenario.

To achieve the above mentioned goals, it is necessary to be able to numerically quantify the amount of herd immunity present in a network. Therefore, we also develop an ‘area under curve (AUC)’ measure, which is able to quantify herd immunity as a value between 0.0 and 1.0. This measure is central to all the analysis we present in this paper, and an independent contribution in itself.

The rest of this paper is organised as follows: In Sect. 2, we present the background of this study by describing existing work in the area of epidemic spread on social networks in general, and comparison of vaccination strategies in particular. In Sect. 3, we describe our simulation set-up. In Sect. 4, we introduce the AUC measure which we will use to quantify the herd immunity of a network. In Sect. 5, we present our results, addressing the above mentioned research questions we set out to answer. In Sect. 6 we discuss our results, present our conclusions and discuss limitations and future work.

2 Background

In the epidemiological domain, a few studies have successfully modelled epidemic spread as a specific example of percolation in networks (Newman and Watts 1999; Newman 2002b; Meyers et al. 2003, 2005, 2006; Sander and Warren 2002). The percolation theory is attractive because it provides connections to several well-known results from statistical physics, in terms of percolation thresholds, phase transitions, long-range connectivity, and critical phenomena in general. For instance, Newman and Watts (1999) suggested using a site percolation model for disease spreading in which some fraction of the population is considered susceptible to the disease, and an initial outbreak can spread only as far as the limits of the connected cluster of susceptible individuals in which it first strikes. An epidemic can occur if the system is at or above its percolation (epidemic) threshold where the size of the largest (giant) cluster becomes comparable with the size of the entire population. Similarly, Moore and Newman (2000) used a general model with two simple epidemiological parameters: (1) susceptibility, the probability that an individual exposed to a disease will contact it and (2) transmissibility, the probability that contact between an infected individual and a healthy but susceptible one will result in the latter contacting the disease. They pointed out that if the distribution of occupied sites or bonds is random, then the problem of when an epidemic takes place becomes equivalent to a standard percolation problem on the graph: what fraction of sites or bonds must be occupied before a “giant component” of connected sites forms whose size scales extensively with the total number of sites (Moore and Newman 2000). It has been noted (Meyers 2006) that the percolation of disease through a network depends on both the level of contagion and the structure of the contact network.

A well-studied concept in epidemiological literature is that of herd immunity, first introduced by Anderson and May (1990). This concept explains that due to the topological structure of a social network, the entire network can be guaranteed immunity from an infection by vaccinating a portion of it—as long as the nodes selected for the vaccination are positioned such that they block infection transmission to non-vaccinated nodes. While perfect herd immunity is rarely achievable, the level of herd immunity present in a network can be quantified by the ratio between the proportion of surviving nodes (after an epidemic spread) and the proportion of vaccinated nodes before the epidemic. In retrospect, if a relatively low proportion of vaccinated nodes cause a relatively high proportion of nodes to avoid infection, we may argue that the herd immunity of that network must have been high.

It was shown by Ferrari et al. (2006) (and implied in other works, such as Newman 2002b, before them) that the success of a particular vaccination strategy depends on the particular topology of the network. They compared random vaccination with natural immunization and utilized three classes of topologies: (1) scale-free, (2) random (which they called ‘Poisson’, after the nature of the resultant degree distribution), and (3) small-world. They found that in scale-free networks, natural immunization is a better defence to infection spread compared to random vaccination, whereas in small-world networks, random vaccination performs better than natural immunisation in containing infection spread. There was no considerable difference between strategies in the case of random networks with Poisson degree distribution. Building on this work, we also ask the following questions: How the growth of the network affects the fraction of survival in each of these classes of networks, and which vaccination strategy is best suited to contain the spread of infection in each case, given that the network is undergoing growth? What are the topological metrics which are relevant in each of the above mentioned classes, and how do they affect immunity? In addition to the above mentioned vaccination strategies, we consider betweenness centrality-based (Freeman 1977, 1979) vaccination. While this later strategy needs complete contact information to be effective, unlike random vaccination, we will show that it warrants consideration by virtue of much better performance. In any case, social networks can be studied at different levels of abstraction (networks of individuals, townships, countries, schools, organizations, etc.), and contact information may be easily obtainable in some cases than others.

3 Simulation design

Following Ferrari et al. (2006), we studied three classes of networks, which have been widely used to simulate spread of epidemics on social networks (Ferrari et al. 2006; Meyers et al. 2003; Moore and Newman 2000; Meyers 2006) and have been shown to represent the topologies of a range of animal and human social networks (Ferrari et al. 2006; Sjoberg et al. 2000). These classes are (1) scale-free networks, which have power law degree distributions (2) Erdos–Renyi random networks, which have poisson degree distributions, and (3) small-world networks, characterised by high clustering coefficient and low average path length. We used a version of the Barabasi–Albert preferential attachment algorithm (Albert and Barabási 1999, 2002; Barabási et al. 2000; Barabási and Bonabeau 2003; Park and Newman 2004) to generate the scale-free networks. To generate the small-world networks, we used the algorithm described by Watts and Strogatz (1998), with rewiring probability $p=0.5$.¹ The ER random networks were generated simply by randomly choosing pairs of nodes and connecting them until the specified number of links have been created. In all classes, we disallowed self links and double links. All network generation and simulation was undertaken using in-house developed software written in Java language.

The epidemics were simulated using the well-known susceptible–infected–recovered model (Ferrari et al. 2006; Newman 2002b; Meyers 2006; Bailey 1957). We used a discrete time synchronous model, in which at each time step nodes can be in ‘susceptible-S’, ‘infected-I’ or ‘recovered-R’ state. We do not distinguish between ‘vaccinated’ and ‘recovered’ states, since we assume that the epidemics studied confer immunity upon recovery. Following Ferrari et al. (2006), we make susceptible nodes become infected across an edge with the binomial probability $p = 1 - e^{(-\beta m)},$ where $m$ is the number of infected nodes to which the considered node is connected, and $\beta$ is the likelihood of transmission across an edge. The nodes are then assumed to recover and enter the immunized state with the probability $\gamma = 0.1$. Thus, the average period of infection for an infected node is ten timesteps. Once the immunity is conveyed, it lasts for the rest of the simulation. At the beginning of the simulations, all nodes are susceptible.

The growth of networks was simulated by simply re-invoking the relevant growth algorithms on existing networks, with a specified number of extra nodes and extra links, while maintaining the vaccination states of existing nodes. All new nodes added were assumed to be in ‘susceptible (S)’ state. The growth percentage was converted into number of additional nodes by multiplying it with the current network size, and the number of additional links were calculated by maintaining the average degree (link-to-node ratio) of the existing network.

We simulated three vaccination strategies: (1) natural immunization, (2) random immunization, and (3) betweenness-based immunization. Natural immunization is the scenario where a previous epidemic leaves parts of the network immunized to further epidemics. To simulate this, we infected a randomly selected node (we averaged over 100 random starting points) and let the epidemic spread for $T_p$ timesteps. $T_p$ was sufficiently large compared to the size of the network to allow the epidemic to spread to all parts of the network. Random immunization was done by randomly selecting a certain number of nodes and ‘vaccinating’ them by setting their immunization state to ‘R’. Similarly, betweenness-based vaccination was done by calculating the betweenness centrality of all nodes, sorting them in the order of betweenness, and vaccinating a given proportion of nodes by setting their immunization state to ‘R’.

Betweenness centrality (Freeman 1977, 1979; Dorogovtsev and Mendes 2003; Kepes 2007) is a well-known centrality measure. Let us note for completeness here that the betweenness centrality measures the fraction of shortest paths that pass through a given node, averaged over all pairs of nodes in a network. It is formally defined, for a directed graph, as

$$\begin{aligned} \mathrm{BC} (v) = \frac{1}{(N-1) (N-2)}{ \sum _{s \ne v \ne t} {\frac{\sigma _{s,t}(v)}{\sigma _{s,t}} }} \end{aligned}$$

(1)

where $\sigma _{s,t}$ is the number of shortest paths between source node $s$ and target node $t$, while $\sigma _{s,t}(v)$ is the number of shortest paths between source node $s$ and target node $t$ that pass through node $v$.

Once a certain portion of the network has been vaccinated by any of the above strategies, we simulated a secondary epidemic, and let it run its course, by iterating for $T_s$ timesteps, where $T_s$ was sufficiently large compared to the network size. Since we used varying network sizes on the order of $10^3$, the values of $T_p$ and $T_s$ also varied, as explained below. We used a range of $\beta$ values to immunize various proportions of network in the case of natural immunization (from 0.01 to 0.5). For the secondary infection simulation, it was set at $\beta =0.4$.

4 AUC measure for quantifying herd immunity

To understand the levels of herd immunity present within a network, we vaccinate a proportion of the network, and simulate the secondary infection, and then measure the proportion of nodes never affected (infected) by the secondary infection. In measuring the proportion of surviving nodes, we only consider the non-vaccinated nodes (the residual network). By varying the proportion of nodes vaccinated, several datapoints can be obtained and plotted. Such a plot gives us a visual idea of the levels of herd immunity in a network (see Fig. 1). If herd immunity is high, lower vaccination proportions will result in higher surviving proportions: if herd immunity is low, this will not happen.

In addition to using plots of proportion of surviving nodes against proportion vaccinated, we introduce an AUC measure to quantify herd immunity in networks. The intention of this measure is to use the area under the proportion surviving–proportion vaccinated curve as a measure of herd immunity in networks. This makes intuitive sense, since if the herd immunity is high, then a lower proportion of vaccination will result in a higher proportion of nodes surviving, and this effect needs to be considered across the range of possible vaccination proportions. Similar AUC measures are used in a number of disciplines. For example, in signal detection theory, the area under a receiver operating characteristic (ROC) curve (Hanley and Mcneil 1982) denotes the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one. The curve is generated by plotting the fraction of true positives out of the positives against the fraction of false positives out of the negatives; therefore, both quantities are fractions. Similarly, the robustness of a complex network against sustained targeted attacks is measured by a ‘robustness coefficient’ (Piraveenan et al. 2013) which is an ‘AUC’ measure.

However, in this case, due to finite size effects in a real-world network, and the nature of some vaccination strategies (such as natural immunization), it is not always possible to consider fixed equidistant points in the ‘percentage infected’ axis. Therefore, we estimate the AUC as follows:

We sort our data points in increasing order of $x$-values (‘percentage vaccinated’) and consider the trapeziums formed by pairs of points. For example, the trapezium we consider between points $(x_1,y_1),(x_2,y_2)$ will have edges of $[(x_1,y_1),(x_2,y_2)]$, $[(x_2,y_2),(x_2,0)]$, $[(x_2,0),(x_1,0)]$ and $[(x_1,0),(x_1,y_1)]$, where a pair of points denote the straight line that connects them. Such trapeziums are shown in Fig. 1, with areas of each trapezium marked as $a_i$ or $b_i$. We sum the areas of such trapeziums and divide the sum by $100^2$ to normalize (if the fractions are in percentage), so that the result is a fraction between 0.0 and 1.0. Of course, there is no guarantee that the corresponding $y$-values (‘percentage surviving’) will be in increasing order, and, therefore, it could be argued this estimate will have an ‘error’. However, given that there will be sufficiently large amount of points, this error will be minimal. The alternative is to fit a curve to the data points and calculating the area under it. While in this way we can accurately measure the area under the curve, the fitting process itself will have an error. Essentially, since we are computing the ‘area’ under a cloud of points which do not all fall on a curve with a corresponding mathematical function, there is no exact answer. Thus, we consider our approach reasonable. The measure is computed as

$$\begin{aligned} \mathrm{AUC} = \frac{0.5 {\sum \nolimits _{i=1}^{n-1}(x_{i+1} - x_i)(y_{i+1} + y_i)}}{100^2} \end{aligned},$$

(2)

where $x_i$ is the vaccinated percentage and $y_i$ is the surviving percentage from data point $i$, and there are $n$ data points. Note that we do not need to normalize by $n$ to make the estimate since the more data points we have, the smaller the ‘widths’ of the trapeziums will be.

Fig. 1

An example demonstrating how the AUC measure is calculated. The proportion of surviving nodes is plotted against the proportion of nodes vaccinated originally, both in percentages. The vaccinated nodes were excluded in calculating the proportion of surviving nodes. It can be seen from the figure that network B responds poorly and network A responds well to vaccination. The AUC is calculated by considering the trapeziums formed by adjacent points and summing the area of these trapeziums. Thus $AUC_A = \sum \nolimits _{i=1}^{10}{a_i}$ and $AUC_B = \sum \nolimits _{i=1}^{10}{b_i}$. The AUC measure returns 0.218 for network B and 0.906 for network A, which reflects this

An example of the utility of the measure is shown in Fig. 1. Let us consider two hypothetical networks, A and B, which need not have the same size. Let us say we vaccinate a certain proportion of nodes in each network, using the same vaccination strategy X, and simulate the epidemic on the networks after the vaccination as described in the previous section. After $T_s$ timesteps, we measure the proportion of nodes that never contacted the infection, excluding the nodes that were vaccinated from the calculation (i.e, the proportion of survivors in the residual network is measured). We do this multiple times, with varying proportions of vaccination, and plot the results, as shown in the figure. From the figure, it can be seen that, in case of network B, higher rates of vaccination still result in lower rates of survivors, until the vaccination proportion approaches 100 %. Meanwhile, in network A, even a relatively small proportion of vaccination results in near complete survival. Therefore, the ‘area’ under the imaginary plot connecting data points belonging to A is much higher than that of B. This is reflected by our AUC measure, which returns $0.906$ for network A and $0.218$ for network B. Thus, the measure is able to quantify what we can visually observe. The advantages of this particular measure are that it does not depend on the number of data points available, does not insist that they be equidistant does not require same size or topology between networks to compare them. It can equally be used to compare two vaccination strategies on the same network. However, it should be clearly understood that we are using the term ‘AUC’ not in the strictest sense but to estimate the ‘area’ under a cloud of points.

5 Simulation results

5.1 Comparing vaccination strategies

We first set out to verify the results of Ferrari et al. (2006) regarding the relative performance of natural immunization and random vaccination and compare them with betweenness-based vaccination. Therefore, we synthesized scale-free, ER random, and small-world networks, each of size 5,000 nodes and 10,000 links. In the case of scale-free networks, the power law exponent was $\gamma =2.0$ approximately. We simulated each vaccination strategy and secondary infection spread as described above. We varied the proportion vaccinated and measured the fraction of nodes surviving (i.e nodes that never contacted the infection in the secondary epidemic) in each case.

Fig. 2

The fraction of surviving nodes against the proportion of vaccinated (or immunized) nodes in three classes of networks. a Scale-free networks, b Erdos–Renyi random networks and c small-world networks. We used networks of size $N=5 \times 10^3$ nodes. Each data point is the average of 100 different initialisations on a particular network with a particular proportion of vaccination. The red stars indicate betweenness-based vaccination, the blue plusses indicate natural immunization while the dark blue crosses indicate random vaccination (colour figure online)

Table 1 The AUC corresponding to Fig. 2 for the three classes of networks and the immunization strategies

Our results are shown in Fig. 2. Each data point in the figure consists of averaging over 100 initialisations of secondary infection over the same vaccinated network. Varying the proportion of vaccination, we undertook 100 different vaccinations for betweenness-based strategy, and 500 different vaccinations for random strategy. The primary infection-based vaccination was also simulated 500 times. The latter two were done more times, since betweenness-based vaccination is ordered and a node vaccinated during a lower-proportion run will not be left out on a higher proportion run. This is not the case for other vaccination strategies, and we, therefore, needed more data points to get a clearer picture.

Figure 2 confirms the results reported by Ferrari et al. (2006): that in scale-free networks, natural immunization confers higher herd immunity than random vaccination, for the same proportions vaccinated—while the opposite is true for small-world networks. In the case of ER random networks, the herd immunity conferred is similar for random vaccination and natural immunization. However, in addition, our results demonstrate that betweenness-based vaccination is the better strategy in all three classes of networks. In fact, it is a far superior strategy if the network is randomly connected, and still a much better strategy if the network is scale-free or small-world. This is a very important result, since it demonstrates that regardless of the topology of the network, a betweenness-based immunization strategy is the best among the studied vaccination strategies to confer herd immunity on a social network. However, it should be noted that for this vaccination strategy to be implemented, a good contact network model needs to be available. This may yet be possible in small and well-monitored communities, such as schools (Salathe et al. 2010), or in social networks with a higher level of abstraction, such as a network of townships.

To better quantify the results we observed above, we apply the AUC measure that we developed. The results are shown in Table 1. From Table 1, we could see that the betweenness strategy is most useful in the randomly connected network, where the difference between it and the next best strategy is almost 35 %.² Whereas in scale-free networks, the betweenness-based strategy is 15 % better than the next best strategy, which is natural immunization, and in small-world networks, betweenness-based strategy is 12 % better than the next best strategy, which is random vaccination. Moreover, we can see that in scale-free networks, natural immunization is 31 % better than random vaccination, while in small-world networks, random vaccination is 37 % better than natural immunization. Interestingly, the last two numbers are similar. Thus we are able to better quantify the qualitative result reported in Ferrari et al. (2006) about the relative merits of these two vaccination strategies.

5.2 Analysing the influence of topological parameters

In the subsection above, we saw that different classes of topologies respond differently to various vaccination strategies. However network topologies can be quantified better than by just differentiating them into classes. Indeed, a whole plethora of metrics are available to do this, and some of them are clustering coefficient, network diameter, assortativity, modularity, average path length, rich-club coefficient, etc. (Albert and Barabási 2002; Park and Newman 2004; Dorogovtsev and Mendes 2003; Zhou and Mondragón 2004; Solé and Valverde 2004). Not all of these metrics are relevant in each class of networks: however, we were interested in more deeply understanding the influence of topology using some of the relevant metrics in each class.

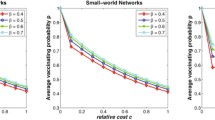
Let us start with small-world networks. Small-world networks typically do not display a big range of assortativity values, since high assortativity leads towards lattice like structures with high clustering but also high path lengths, while high disassortativity leads towards star like structures with short path lengths yet low clustering. Therefore to maintain smallworldness the network should be non-assortative. For similar reasons, it could be argued that there will be not much variation in modularity or rich-club coefficient in small-world networks. Thus, the metrics we are interested in are clustering coefficient and network diameter. Since small-world networks are characterised by relatively small characteristic path lengths and high clustering, the ‘small-worldness’ of these networks is typically measured by their diameter and clustering coefficient. Is there a connection between these parameters and herd immunity of networks?

To answer this, we generated an ensemble of families of small-world networks. Each family had a fixed clustering coefficient and diameter. We compared the herd immunity of these networks by plotting the percentages of vaccination and survival, as well as utilising our AUC measure. For example, Fig. 3 shows four such networks drawn from different families, with differing characteristics. From the figure, it is clear that the higher the clustering coefficient, and the lower the diameter, the lower the herd immunity. This is confirmed by Table 2, where the AUC measure is averaged over one hundred networks of the same family in each case. These figures and table give rise to an important finding: the small-worldness hinders the presence of herd immunity. The more ‘small-world’ a community is, the less ability it has to protect its members from infection by utilising herd immunity. This is a very important finding, since, as mentioned before, most social networks in real-world display small-world feature to various degrees. However, it should be remembered that network density (links to node ratio) is fixed in the above experiments. If the ‘small-worldness’ is achieved by simply throwing in more links, which can both increase clustering and decrease path lengths at the same time, it is intuitively clear that it could only help the infection spread rather than prevent it. More contacts naturally result in faster infection spread. The key finding here though is that even if the number of contacts is fixed, the signature ‘small-world’ features hinder community protection.

Fig. 3

The influence of ‘small-worldness’ in the herd immunity of small-world networks. The small-world effect is measured by network diameter and clustering coefficient. The plot shows percentage of survivors against percentage vaccinated for a betweenness-based vaccination, b natural immunization, and c random vaccination

Table 2 The AUC for small-world networks of differing parameters under differing vaccination strategies

Fig. 4

The influence of assortativity in the herd immunity of scale-free networks. The figure shows AUC of the percentage survived–percentage vaccinated curve for a betweenness-based vaccination, b natural immunization, and c random vaccination

Now let us turn our attention to scale-free networks. Scale-free networks have fairly heterogeneous degree distributions (Albert and Barabási 2002; Dorogovtsev and Mendes 2003): thus, mixing patterns of nodes in terms of number of links become relevant. Therefore, we study the influence of assortativity on herd immunity in scale-free networks. Assortativity is typically used to quantify the average similarity between nodes connected by links in a network. The more similar connected nodes are, the more assortative the network becomes. Even though this similarity can be measured in terms of any node attribute, typically it is measured in terms of node degrees, so that the assortativity of a network is influenced by its topology alone and thus becomes a metric similar in that sense to network diameter, clustering coefficient etc.

Formally, assortativity has been defined as a correlation function of the excess degree distribution and link distribution of a network (Solé and Valverde 2004; Newman 2003). The concepts of degree distribution $p_k$ and excess degree distribution $q_k$ for undirected networks are well known (Solé and Valverde 2004). Given $q_k$, one can introduce the quantity $e_{j,k}$ as the joint probability distribution of the remaining degrees of the two nodes at either end of a randomly chosen link. Given these distributions, the assortativity of an undirected network is defined as (Solé and Valverde 2004; Newman 2003, 2002a):

$$\begin{aligned} r=\frac{1}{\sigma _q^2 }\left[ { \sum \limits _{jk} {jk\left( {e_{j,k} -q_j q_ k} \right) } } \right] \end{aligned}$$

(3)

where $\sigma _q$ is the standard deviation of $q_k$.

We studied the influence of assortativity on herd immunity by considering scale-free networks, since small-world networks (generated using the Watts–Strogatz model) and random networks tend to have not much variation in terms of assortativity. In the case of scale-free networks though, the ‘scale-free’ nature can be preserved by preserving the degree distributions, and there are well-known algorithms to change the assortativity of a network while preserving the degree sequence, particularly when extreme assortativity values are not required. We used the algorithms described by Newman (2002a, 2003) to generate networks with varying assortativity values, starting from scale-free networks with power-law degree distributions and a scale-free exponent of $\gamma = 2.0$. We kept the assortativity range from $-0.3$ to $+0.3$, partly because extreme values are rarely observed in real-world social systems and partly to prevent decomposition of the network into components.³ Then we simulated contagion spread on the resulting networks as described before and considered the proportion survived vs proportion vaccinated curves.

We avoid showing the plots themselves in this paper, since there is not much difference between the plots for each assortativity value and it is difficult to tease out the results. However, this is exactly when the quantifiable AUC measure can be most useful. Therefore, we computed the AUC for each of the experiments, and in Fig. 4, we plot these AUC against assortativity values for several networks for each of the vaccination strategies. The results are rather more clear and interesting. It appears that, in all forms of vaccination, herd immunity increases with assortativity. The disassortative networks, therefore, are harder to immunize, while the assortative networks are easier. This result is also-counter intuitive, since disassortative networks tend to have many ‘star’ motifs, and it could be expected that by vaccinating the hubs in these stars, the rest of the motif could easily be immunized. We should also note that while there is a clear trend for all vaccination strategies, the difference in AUC is rather small between various levels of assortativity for betweenness-based vaccination, whereas for random immunization or natural immunization, the difference is considerable. It may be that the influence of mixing patterns, a topological aspect, is minimised by a strategy which actively considers topology.

As a complementary approach of quantifying the influence of mixing patterns on herd immunity, we now consider the ‘rich-club coefficient’ of networks and how they correlate to the levels of herd immunity present within the networks. The rich-club coefficient gets its name from the fact that it measures the so-called ‘rich-club phenomena’ within the network—to what extent highly connected nodes preferentially connect to other highly connected nodes, compared to what could be expected in random mixing (Zhou and Mondragón 2004; Sabidussi 1966; Zhou and Mondragón 2003). Formally, a rich-club coefficient is defined in terms of degree-based rank $r$ of nodes, and the rich-club connectivity $\varphi (r)$. The degree-based rank denotes the rank of a given node when all nodes are ordered in terms of their degrees, highest first. This is then normalised by the total number of nodes (and can be given in percentages: for, e.g., $r=10\,\%$ means the ‘best’ 10 % nodes in terms of degree are considered). The rich-club connectivity or coefficient is defined as the ratio of actual number of links over the maximum possible number of links between nodes with rank ‘higher’ than $r$. Thus, it is possible to calculate the rich-club connectivity distribution of a network, $\varphi (r)$ over $r$. Equation 4 shows the formal definition of the rich-club coefficient.

$$\begin{aligned} \varphi (r)=\frac{2E(r)}{r (r-1)}. \end{aligned}$$

(4)

Here, $E(r)$ is the number of links between the $r$ nodes and $r(r-1)/2$ is the maximum number of links that these nodes have share. The interpretation of the rich-club coefficient is that the higher this coefficient, the higher the tendency for ‘rich’ nodes to preferentially connect to each other. Therefore, it measures an aspect of assortativity. Of course, assortativity could also be increased by ‘poor’ nodes preferentially connecting to each other. However, if ‘richer’ nodes prefentially connect to each other, then for a given network density, ‘poorer’ nodes also would be forced to mix more among themselves. Therefore, the assortativity coefficient and rich-club coefficients tend to be correlated.

Again, we consider a set of scale-free networks which have the same degree distribution yet differing mixing patterns. In fact, the set of networks we consider is the same set that we considered in understanding the influence of assortativity; however, we now measure the rich-club coefficient instead of assortativity. Since the rich-club coefficient is not a single measure and depends on the relative size of the rich-club considered, we consider the 5 % rich-club and the 10 % rich-club in this study, without loss of generality.⁴ Again, we simulate infection spread according to the three strategies, plot the proportion surviving against the proportion vaccinated for each network, and compute the AUC. Thereafter, we plot the AUC against the rich-club coefficients $\varphi (r)$ as shown in Fig. 5.

From the figures, we again find that the AUC values are correlated with the rich-club coefficients. This is clearly observable for all strategies, and for both 5 and 10 % coefficients. Therefore, we can conclude that the more ‘rich-club tendencies’ a network displays, in terms of node degree, the higher its herd immunity going to be, all other things being equal.

Fig. 5

The influence of rich-club coefficient in the herd immunity of scale-free networks. The figure shows AUC of the percentage survived–percentage vaccinated curve for a betweenness-based vaccination 5 % rich-club coefficient, b natural immunization 5 % rich-club coefficient, c random vaccination 5 % rich-club coefficient, d betweenness-based vaccination 10 % rich-club coefficient, e natural immunization 10 % rich-club coefficient and f random vaccination 10 % rich-club coefficient. Since rich-club coefficient is a measure that depends on the relative size of the ‘rich-club’ considered, here we are considering the 5 % rich-club and the 10 % rich-club only, which are indicative of the overall rich-club tendency

From the results we obtained considering both assortativity and rich-club coefficient in scale-free networks, we can come to the important conclusion that preferential mixing plays an important part in increasing the herd immunity of networks. While this is true for all strategies, it is particularly evident when strategies which are not directly guided by topology are used. The actual difference preferential mixing can make, all other things being equal, is small however, and it is our use of the AUC measure which made it possible to come to this conclusion. This result means that, the herd immunity of a social system can be increased, not only by people reducing their links or contacts (which, it is trivial to see, would discourage contagion spread and thereby increase herd immunity), but also by people changing their contact patterns while maintaining the number/frequency of contacts (maintaining the degree distribution, in network parlance). If most people maintain links with others who maintain similar number of links, this increases the community protection inherent in the system.

Finally, in the case of random networks, we did not undertake any in-depth analysis in terms of topology. Random networks, by definition, are not supposed to have that much variation in terms of network metrics such as clustering, assortativity, etc. If a growth process introduces variation, then the network is no longer ‘random’ in terms of topological connections. Therefore, further analysis of topology in this class is less warranted.

5.3 Measuring the influence of network growth

Social networks undergo constant growth. New members are added into the community by birth, immigration, admission, employment, etc., depending on the type of social network we consider. Often, these new members come without the required vaccination against particular illnesses. This is particularly true if the vaccination considered is not the one administered to all children after birth (in which case the concept of herd immunity is irrelevant anyway), but a one-off vaccination administered to part of a community against a newly discovered or introduced illness. In this case, migrants who come into the community from other regions or countries are not likely to have the vaccination. In any case, even if no new members are added to the community, growth can still occur by new interactions (links) being created between existing members, and these additions are going to have an affect on the herd immunity of the network. Therefore, in this section we study the affect of growth on the three classes of topologies we considered.

To quantify the influence of network growth on herd immunity levels, we simulated growth in each class of networks by increasing the number of nodes by (1) 0, (2) 20, (3) 50, and (4) 100 %. The nodes were added by again using the original algorithm utilised to synthesise each class of networks—i.e scale-free networks were ‘grown’ using preferential attachment, random networks were grown by adding nodes and randomly making links to existing nodes, and small-world networks were grown using the algorithm described by Watts and Strogatz (1998). We added links such that the average degree of each network was maintained. The vaccination status of the original nodes was maintained, while new nodes were added with state ‘S’ (suscpetible). Each ‘original’ network was of the size $N$ =11,000 nodes and $M$ = 2,000 links. We simulated infection spread for $T_s = 200$ timesteps, which is much higher than the diameter of each of these networks so that we may assume infection will have time to reach all parts of the network, and we used $\beta = 0.4$. The same number of timesteps was used in each growth scenario. We again simulated the three types of vaccination/immunization strategy. We assume that after $T_s$ timesteps enough vaccination resources can be put in place to vaccinate the entire community to prevent further spread—thus, regardless of the varying network sizes, we are interested in studying the survival (non-infection) rates within a bounded time.

We may expect two competing factors at work here: (1) The increase in network size with same number of timesteps makes it harder for infection to spread to all parts of network, so the survival percentage might increase. (2) The increase in size with same number of vaccinated nodes will make the density of vaccination/immunization less, so the survival percentage might decrease. In the following analysis, we demonstrate how the result of the interplay between these two factors depend on network topology.

Fig. 6

The fraction of surviving nodes against the proportion of vaccinated (or immunized) nodes in three classes of networks for betweenness-based vaccination strategy. a Scale-free networks, b Erdos–Renyi random networks and c small-world networks. Four levels of network growth are shown. We used networks of size $N=1.0 \times 10^3$ nodes. Each data point is the average of 20 different initialisations on a particular network with a particular proportion of vaccination. The red plusses indicate no growth, the green crosses indicate 20 % growth, the blue stars indicate 50 % growth, while the pink squares indicate 100 % growth (colour figure online)

Table 3 The AUC for networks after growth and betweenness-based vaccination, corresponding to Fig. 6

Our results for the betweenness-based vaccination strategy are shown in Fig. 6, and corresponding AUC values are shown in Table 3. In the figure, the survival percentages are plotted against the original vaccination percentages (so as to keep the $x$ axis comparable) for 0, 20, 50, and 100 % growth. We may see that in all classes, the growth initially results in lower survival rates, presumably due to lower vaccination density. However, the ER random networks show a fundamentally different tendency. In scale-free and small-world network, increased growth results in decreased survival rates for same (initial) vaccination rates. However, in ER random networks, after the initial decline, further growth tends to increase the survival rate. This must be due to the increased difficulty in reaching further parts of the network. According to Table 3, for ER random networks, while no growth results in 78.5 % immunity, a 20 % growth results in 48.9 % immunity which is less, but a 50 % growth results in 53.9 and 100 % growth results in 66.2 % immunity which shows an increasing trend. However, the corresponding analysis for scale-free and small-world networks show steadily decreasing numbers (93.2, 87.9, 73.8, and 47.8 % for scale-free and 86.9, 70.2, 53.1, and 38.4 % for small-world). We may surmise that the topology of random networks, with the lack of dominant hubs and low clustering, means that despite the lower density of vaccinated nodes, the infection does not spread easily in growing networks. In scale-free and small-world networks, on the other hand, growth makes it easy for infection to spread. We may also observe small-world networks and scale-free networks show similar levels of adverse impact to growth (according to Table 3, a 100 % growth results in 45.4 % AUC reduction in scale-free networks, while the same growth results in 48.5 % AUC reduction in small-world networks).

Fig. 7

The fraction of surviving nodes against the proportion of vaccinated (or immunized) nodes in three classes of networks for random vaccination strategy. a Scale-free networks, b Erdos–Renyi random networks and c small-world networks. Four levels of network growth are shown. We used networks of size $N=1.0 \times 10^3$ nodes. Each data point is the average of 20 different initialisations on a particular network with a particular proportion of vaccination. The red plusses indicate no growth, the green crosses indicate 20 % growth, the blue stars indicate 50 % growth, while the pink squares indicate 100 % growth (colour figure online)

Table 4 The AUC for networks after growth and random vaccination, corresponding to Fig. 7

Fig. 8

The fraction of surviving nodes against the proportion of vaccinated (or immunized) nodes in three classes of networks for natural immunization. a Scale-free networks, b Erdos–Renyi random networks and c small-world networks. Four levels of network growth are shown. We used networks of size $N=1.0 \times 10^3$ nodes. Each data point is the average of 20 different initialisations on a particular network with a particular proportion of vaccination. The red plusses indicate no growth, the green crosses indicate 20 % growth, the blue stars indicate 50 % growth, while the pink squares indicate 100 % growth (colour figure online)

Table 5 The AUC for networks after growth and natural immunization, corresponding to Fig. 8

Now let us turn our attention to random vaccination. Our results for this strategy are shown in Fig. 7, and the corresponding AUC values are shown in Table 4. We find a similar set of results to betweenness-based vaccination. That is, in both scale-free and small-world networks, growth results in decreasing proportions of surviving nodes, since growth decreases vaccination density. However, in the case of ER random networks, the survival rate initially decreases with growth, then begins to increase. We see that for a 100 % growth, the survival rate is even better than that of the original network when the vaccination rate is small.

Finally, let us consider natural immunization. To simulate natural immunization, we let the infection run its course on each network for $T_p = 200$ timesteps, which is much higher than the diameter of the networks in each case, and we used a low beta value ($\beta =0.01$). Then we simulated network growth and secondary infection spread as described before. Our results are shown in Fig. 8, and the corresponding AUC values are in Table 5. We may again see that in the case of ER random network, a 20 % growth reduces the fraction surviving for all vaccinated proportions, but further growth actually increases the fraction surviving. Furthermore, in both scale-free and small-world networks, the growth results in the surviving fraction decreasing, as it happened for other vaccination strategies. However, we can also observe that in the case of small-world networks, a 20 % growth does not decrease the survival fraction (61.8 vs 66.5 %, according to Table 5). The small-world network immunized by prior epidemics seems to be robust to insignificant growth. However, when the growth becomes significant, the survival fraction does decrease for all proportions of immunization.

Fig. 9

The fraction of surviving nodes against the proportion of vaccinated (or immunized) nodes in three classes of networks, after networks have gone through 100 % growth. a Scale-free networks, b Erdos–Renyi random networks and c small-world networks. We used networks of original size $N=1.0 \times 10^3$ nodes (therefore, the results shown are for networks of 2,000 nodes each). Each data point is the average of 20 different initialisations on a particular network with a particular proportion of vaccination. The red filled squares indicate betweenness-based vaccination, the blue crosses indicate natural immunization while the dark blue squares indicate random vaccination (colour figure online)

We have seen that, as demonstrated by Ferrari et al. (2006), when there is no growth, natural immunization is a better strategy than random vaccination in scale-free networks, and vice-versa in small-world networks. How the growth of these networks will impact on this observation? To verify this, we use the results already shown in Figs. 6, 7, and 8 but plot them in different configuration for easy comparison. As such, we plot the results of all three vaccination methods after 100 % growth for each class of networks in Fig. 9. We chose the 100 % growth to demonstrate the extreme case. The corresponding AUC values are shown in Table 6, which again draws values from Tables 3, 4 and 5 but orders them in a different way for easy comparison. We may see from these figures and table that the difference between strategies become less pronounced after the networks have undergone growth. Indeed, in the case of small-world networks, the three vaccination strategies are indistinguishable after a 100 % growth (0.365, 0.405, and 0.384 in AUC measure, respectively). Comparing this result with Fig. 2 and Table 1, we may see that the advantage enjoyed by betweenness-based immunization and random immunization over natural immunization has been nearly totally eliminated by the growth. It is a similar scenario with ER random networks, as shown in Fig. 7. However, as was earlier shown in Fig. 2, even without growth the random and natural vaccination did not give very different results in the case of ER networks. The better performance enjoyed by betweenness-based vaccination, however, has been nearly eliminated by growth. In the case of scale-free networks, however, we may see that the betweenness-based vaccination strategy still performs better than the natural immunization and random immunization strategies, in that order. Also, the differences between these strategies have been not blunted by the growth. Whereas the betweeness strategy was 15 % better than the next best strategy before growth (as shown earlier), it is now 151 % better than the next better strategy (0.478 over 0.190 represents a 151 % increase).

Table 6 The AUC for networks after growth under differing vaccination strategies

We can come to an important conclusion from these observations. Among the three classes of networks studied, it is the scale-free class where the vaccination strategy matters the most, despite the growth. If we consider rapidly growing random or small-world networks, then it is unnecessary to implement a particular vaccination strategy, since after the growth all strategies will deliver similar results. Since a betweenness-based strategy needs topological information and random vaccination strategy does not, going through the trouble of constructing a contact network administering vaccination based on that makes sense only in scale-free networks, if the network is rapidly growing. However, for slowly growing or non-growing networks, computing betweenness makes sense regardless of the topology, since for all three classes of networks a betweenness-based strategy is best.

6 Conclusions

In this paper, we analysed the interplay between network topology and vaccination strategies and their influence in determining the level of herd immunity present in different classes of social networks. We also introduced an ‘AUC’ measure which can quantify the level of herd immunity present in a network after a particular strategy of vaccination was applied. Using synthesized networks of different classes, we first confirmed the result already reported in literature that natural immunization confers higher herd immunity than random vaccination in scale-free networks and the reverse is true for small-world networks. We then showed that, if the topology of the contact network is known, a betweenness-based vaccination strategy is far superior than both natural immunization and random vaccination for all classes of networks. We discussed the implications of this result.

Analysing the influence of topology deeper, we showed that in small-world networks, the so-called features conferring ‘small-worldness’ (high clustering and low diameter) reduce the amount of herd immunity, all other things being equal. Thus, social networks which show these characteristics are harder to defend using community protection. We also showed that in scale-free networks, the role of preferential mixing patterns, measured by ‘assortativity’ and rich-club coefficient, is to aid community protection. The more preferential the degree-based mixing, the higher the level of herd immunity in a network. This result is important, because it means that herd immunity of a community can be increased while the frequency distribution of number of connections (degree distribution of a network) is preserved. However, the difference made by preferential mixing is minimal when a betweenness-based vaccination strategy is used.

Noting that real-world social networks constantly undergo growth, we then analysed the effect of network growth on herd immunity. We argued that two opposing influences can be exerted by network growth on herd immunity—the lessening density of vaccination may reduce herd immunity, while the increasing path lengths may boost it. We found that in the case of random networks, moderate growth decreases herd immunity, while substantial growth actually increases it, since infection is unable to spread to all parts of network quickly enough in the absence of hubs.⁵ In the case of both small-world and scale-free networks however, we showed that any growth results in decreasing herd immunity.

We also compared the effect of growth on differentiating between vaccination strategies. We showed that in both random networks and small-world networks, substantial growth renders the original vaccination strategy irrelevant. We found that only if the network is scale-free, choosing a better vaccination strategy originally would still yield benefits after the network has grown substantially.

Even though our analysis was based on synthesized networks, several of the results we observed here are of significance: first, the fact that the ‘small-worldness’ in social systems hinders community protection, other things being equal, means that an inherent feature observed in many societies helps infection spread. While the degree distribution of a network can be changed considerably by ‘taking out’ (vaccinating/removing/quarantining) a few hub nodes, it is not very easy to decrease the ‘small-worldness’. This can be done only by removing several links and thereby reducing clustering, or strategically removing a few selected links which connect long, distant nodes (if these links can be located), thereby increasing path lengths. The other observation was that in scale-free networks, preferential mixing helps vaccination strategies to various extents. This suggests that certain vaccination strategies can work better if individuals merely change their interaction patterns (while keeping their frequency of interaction), to mix more preferentially with ‘similar’ individuals in terms of degrees. Particularly, in terms of ‘random’ vaccination, which represents the current clinical vaccination processes in the sense that they are random from a topological perspective, it is interesting to note that the more ‘famous’ individuals choose to interact with other ‘famous’ individuals, the better it would work. Finally, we saw that in both scale-free and small-world networks, growth hinders community protection as expected. However, if the society displayed a random topology, then growth can apparently help ‘dilute’ the infection spread, and the overall proportion of people affected might be less.

This research is not without its limitations. We have only considered three levels of growth, moderate to substantial, whereas it would be more illustrative to consider levels of growth as a continuum. We have not considered node deletions, and link deletions, which are also potentially commonplace when a social network is growing. The classes of networks we synthesized, while commonly used by researchers in epidemiology, do not represent real-world networks, and it would be more enlightening to use topologies from real world social networks. Our future work will focus on these directions. Despite these limitations, we believe that the results reported here are of interest to the scientific community.