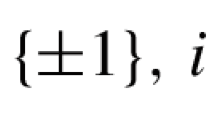Abstract
Clustering methods for multiple graphs explore and exploit multiple graphs simultaneously to obtain a more accurate and robust partition of the data than that using single graph clustering methods. In this paper, we study the clustering of multiple graphs with inter-relation among vertices in different graphs. The main contribution is to propose and develop a block spectral clustering method for multiple graphs with inter-relation. Our idea is to construct a block Laplacian matrix for multiple graphs and make use of its eigenvectors to perform clustering very efficiently. Global optimal solutions are obtained in the proposed method and they are solutions of relaxation of multiple graphs ratio cut and normalized cut problems. In contrast, existing clustering methods cannot guarantee optimal solutions and their solutions are dependent on initial guesses. Experimental results on both synthetic and real-world data sets are given to demonstrate that the clustering accuracy achieved and computational time required by the proposed block clustering method are better than those by the testing clustering methods in the literature.













Similar content being viewed by others
References
Adama JK, Odhavb B, Bhoola KD (2003) Immune responses in cancer. Pharmacol Therap 99:113–132
Bernatsky S, Ramsey-Goldman R, Clarke A (2005) Exploring the links between systemic lupus erythematosus and cancer. Rheum Dis Clin N Am 31(2):387–402
Bickel S, Scheffer T (2004) Multi-view clustering. Proc IEEE Int Conf Data Min 4:19–26
Bones J, Byrne JC, ODonoghur N, McManus C, Scaife C et al (2011) Glycomic and glycoproteomic analysis of serum from patients with stomach cancer reveals potential markers arising from host defense response mechamisms. J Proteome Res 10(3):1246–1265
Cai D, He X, Han J (2006) Tensor space model for document analysis. In: Proceedings of the 29th annual international ACM SIGIR conference on Research and development in information retrieval, ACM, pp 625–626
Chaudhuri K, Kakade S, Livescu K, Sridharan K (2009) Multi-view clustering via canonical correlation analysis. In: Proceedings of the 26th international conference on machine learning, Montreal, ACM, pp 129–136
Collins K, Jacks T, Pavletich NP (1997) The cell cycle and cancer. Proc Natl Acad Sci USA 94:2776–2778
Cheng W, Zhang X, Guo Z, Wu Y, Sullivan P, Wang W (2013) Flexible and robust co-regularized multi-domain graph clustering. In: Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, ACM, pp 320–328
Colotta F, Allavena P, Sica A, Garlanda C, Mantovani A (2009) Cancer-related inflammation, the seventh hallmark of cancer: links to genetic instability. Carcinogenesis 30:1073–1081
Dong X, Frossard P, Vandergheynst P, Nefedov N (2012) Clustering with multi-layer graphs: a spectral perspective. IEEE Trans Signal Process 60(11):5820–5831
Hu H, Yan X, Huang Y, Han J, Zhou X (2005) Mining coherent dense subgraphs across massive biological networks for functional discovery. Bioinform 21(1):213–221
Huang D, Sherman BT, Lempicki RA (2009a) Systematic and integrative analysis of large gene lists using david bioinformatics resources. Nat Protoc 4:44–57
Huang D, Sherman BT, Lempicki RA (2009b) Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists. Nucl Acid Res 37:1–13
Simpson AJ, Caballero OL, Jungbluth A, Chen YT, Old LJ (2005) Cancer/testis antigens, gametogenesis and cancer. Nat Cancer 5(8):615–625
Jegelka S, Sra S, Banerjee A (2009) Approximation algorithms for tensor clustering. In: ALT’09 Proceedings of the 20th international conference on algorithmic learning theory, pp 368–383
Kumar A, Rai P, Daum’e H III (2011) Co-regularized multi-view spectral clustering. NIPS
Kumar A, Daum H III (2011) A co-training approach for multi-view spectral clustering. In: International conference on machine learning
von Luxburg U (2007) A tutorial on spectral clustering. Stat Comput 17(4):395–416
Liu N, Zhang B, Yan J, Chen Z, Liu W, Bai F, Chien L (2005) Text representation: from vector to tensor. In: International conference on data mining
Liu Y, Zhu Q, Zhu N (2008) Recent duplication and positive selection of the gage gene family. Genetics 133:31–35
Liu X, Ji S, Glnzel W, De Moor B (2013) Multi-view partitioning via tensor methods. IEEE Trans Knowl Data Eng 25(5):1056–1069
Long B, Zhang ZM, Wu X, Yu PS (2006) Spectral clustering for multi-type relational data. In: Proceedings of the 23rd international conference on Machine learning, ACM, pp 585–592
Lu H, Ouyang W, Huang C (2006) Inflammation, a key event in cancer development. Mol Cancer Res 4:221–233
Ng M, Li X, Ye Y (2011) MultiRank: co-ranking scheme for objects and relations in multi-dimensional data. In: Proceedings of the 17th ACM SIGKDD conference on knowledge discovery and data mining, pp 1217–1225
Parikh-Patel A, White RH, Allen M, Cress R (2008) Cancer risk in a cohort of patients with systemic lupus erythematosus (sle) in california. Cancer Causes Control 19(8):887–894
Rand WM (1971) Objective criteria for the evaluation of clustering methods. J Am Stat Assoc pp 846–850
Schindelmann S, Windisch J, Grundmann R, Kreienberg R, Zeillingeret R et al (2002) Expression profiling of mammary carcinoma cell lines: correlation of in vitro invasiveness with expression of cd24. Tumour Biol 23(3):139–145
Tang W, Lu Z, Dhillon I (2009) Clustering with multiple graphs. In: ICDM ’09: Proceedings of the 2009 9th IEEE international conference on data mining
Walliams GH, Stoeber K (2012) The cell cycle and cancer. J Pathol 226:352–364
Zhang B, Horvath S (2005) A general framework for weighted gene co-expression network analysis. Stat Appl Gen Mol Biol 4(1). doi: 10.2202/1544-6115.1128
Acknowledgements
M. Ng’s research is supported in part by HKRGC GRF 12302715 and 12306616 and CRF C1007-15GF. S. Zhang’s research is supported in part by NSFC Grant No. 11471082, Science and Technology Commission of Shanghai Municipality 16JC1402600.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Theorem 1
(i) It is clear that \(\mathbf{B}\) is symmetric. Given any \(\mathbf{f} = [\mathbf{f}_1 \mathbf{f}_2 \cdots \mathbf{f}_M ]^T\) with \(\mathbf{f}_m = [ \mathbf{f}_m(1) \mathbf{f}_m(2) \cdots \mathbf{f}_m(N_m) ]^T\), we have
Therefore, \(\mathbf{B}\) is semi-positive definite. On the other hand, it is easy to check that \(\mathbf{B}{} \mathbf{1} = 0{} \mathbf{1}\) where \(\mathbf{1}\) is a vector of all ones.
(ii) We consider \(\mathbf{B}\) as a Laplacian matrix for a graph containing \(\sum _{m=1}^M N_m\) vertices. It is clear that the number of connected components of this graph is equal to the number of inter-components. Using the spectral graph theory, we know that the multiplicity of the zero eigenvalue of \(\mathbf{B}\) is equal to the number of inter-components. \(\square\)
Proof of Theorem 2
Let us define the following K cluster-indicator \(\sum _{m=1}^M N_m\)-vectors \(\mathbf{y}^{(k)}\) (\(k=1,2,\cdots ,K\)) as follows
with
The \(\sum _{m=1}^M N_m\)-by-K matrix \(\mathbf{Y} = [ \mathbf{y}^{(1)}, \mathbf{y}^{(2)}, \ldots , \mathbf{y}^{(K)} ]\) satisfies \(\mathbf{Y}^T \mathbf{Y} = \mathbf{I}_K\). Also, \(\{ \mathbf{y}_m^{(1)}, \mathbf{y}_m^{(2)}, \ldots , \mathbf{y}_m^{(K)} \}\) are orthogonal for \(1 \le m \le M\).
When \(C_m^{(k)}\ne \emptyset\), we note that
for \(1 \le k \le K\) and \(1 \le m \le M\), and
In the first term of (14), \(\Upsilon _{a}(C_m^{(k)})\) refers to the across edges linking \(C_m^{(k)}\) and all vertices in other relations. By dividing \(| C_m^{(k)} |\), it refers to an average inter-degree over each vertex in \(C_m^{(k)}\).
When \(C_m^{(k)}=\emptyset\), it is easy to verify that the following terms will turn to zero:
which indicate that our setting in (9) is satisfied.
It follows that \(trace( \mathbf{Y}^T \mathbf{B}{} \mathbf{Y} )\) is equal to \(J_1( \{C_m^{(1)}, \ldots , C_m^{(K)} \}_{m=1}^{M} )/M\) plus a constant term. This implies optimizing (9) is equivalent to finding a minimum of (6) with a special form of (12). Therefore, (6) is relaxed problem of (9) without imposing a special form. \(\square\)
Proof of Theorem 3
To prove that
is the best partition, we need to show that for any partition
we have
By substituting
into above inequality, we get
Since \(N_1\le N_2\le \cdots \le N_K\), we have \(({\frac{1}{N_1}}-{\frac{1}{N_K}})\ge \cdots \ge (\frac{1}{N_{K-1}}-\frac{1}{N_K})\ge 0\), it follows that partition (15) is the best partition. The theorem is proved. \(\square\)
Proof of Theorem 4
Now we set
similar to (12), and we have \((\mathbf{y}_m^{(k)})^T \mathbf{D}_{m,m} \mathbf{y}_m^{(k)} = 1/M\) for \(1 \le m \le M\) and \(1 \le k \le K\). We can show that
and using the same argument in ratio cut, we obtain
Using the same way to deal with \(C_{m}^{(k)}= \emptyset\) or \(\ne \emptyset\), it follows that \(trace( \mathbf{Y}^T \widehat{\mathbf{B}} \mathbf{Y} )\) is equal to sum of \(J_2( \{ C_m^{(1)}, C_m^{(2)}, \ldots , C_m^{(K)} \}_{m=1}^{M} )/M\) and a constant term. Therefore, (8) is a relaxed problem of (11). \(\square\)
Rights and permissions
About this article
Cite this article
Chen, C., Ng, M. & Zhang, S. Block spectral clustering for multiple graphs with inter-relation. Netw Model Anal Health Inform Bioinforma 6, 8 (2017). https://doi.org/10.1007/s13721-017-0149-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13721-017-0149-6